3. Напружений стан рідини та фундаментальні закони в механіці суцільного середовища

1. Рівняння руху рідини в напруженнях

О держимо загальне рівняння руху рідини, яке встановлює зв’язок між зовнішніми і внутрішніми силами, які діють на неї.

Виділимо в рідині, яка рухається, довільний об’єм V з поверхнею S (рис. _._), а в середовищані нього елементарну рідку частинку з масою dV і поверхнею dS. До цієї частинки прикладені масові сили з напруженням і поверхневі сили з напруженням . Запишемо рівняння руху цієї частинки, позначуючи прискорення її центра ваги ,

, (3.1)

Підсумуємо ліву і праву частини рівняння (3.1). Підсумовування перших двох членів зводиться до інтегрування по об’єму, а третього члену – по площадкам, по яких елементарні частинки зтикаються одна з другою. Згідно третього закону Ньютона поверхневі сили по всім внутрішнім площадкам взаємно компенсуються і остануться лише поверхневі сили по площі S, яка обмежує об’єм V,

, (3.2)

Тут і надалі кратні інтеграли будуть розрізнятися лише індексом, по яким відбувається підсумовування. Перетворимо третій член рівняння (3.2), використовуючи для цього залежність (1.19)

. (3.3)

Застосуємо до правої частини цієї рівності відомі перетворення Гауса-Остроградського, яке встановлює зв’язок між об’ємним і поверхневим інтергалами,

. (3.4)

Підставляючи праву частину (1.37) в рівняння (1.35), одержимо

(3.5)

Всі члени в рівнянні (3.5) інтергуються по об’єму. Рівняння (3.2) і (1.38) є рівняннями руху рідинного об’єму в інтегральній формі. Їх ліва частина уявляє головний вектор сил інерції, перший член правої частини – головний вектор масових сил, а другий – головний вектор поверхневих сил.

Представимо диференціальну форму рівняння руху більш зручну для вивчення руху рідини. Об’єднаємо всі члени рівняння (3.5) під знаком інтеграла шляхом переносу сили інерції праву частину

(3.6)

В зв’язку з довільністю об’єму цей інтеграл обертається в нуль тільки тоді, коли нулю тотожно дорівнює підінтегральна функція

(3.7)

В результаті одержимо диференціальне рівняння руху рідини в напруженнях

(3.8)

яке зв’язує прискорення з напруженнями масових і поверхневих сил в даній точці потоку і справедливе як для в’язкої так і нев’язкої рідини.

Проектуючи векторне рівняння (3.8) на вісі координат, будемо мати

(3.9)

Система рівнянь (3.9) слугує основою для розробки гідродинаміки в’язкої і нев’язкої рідини.

Тензор напружень

(3.10)

2. Закони збереження моменту імпульсу та енергії

Р івняння збереження моменту імпульсів

(3.11)

Рівняння збереження енергії

де Е – повна енергія об’єму W;

де і – потужність сил: 1 – до одиниці маси, 2 – до одиниці поверхні.

,

.

Контрольні запитання

1. .

2. .

3. .

4. .

5. .

6. .

7. .

4. Гідрогазостатика

1. Гідростатика, основи

   1. Сили, що діють в рідині

Гідростатика розглядає закони рівноваги рідин, які знаходяться в стані спокою, і практичне застосування цих законів.

На рідину, яка знаходиться в спокої, діють зовнішні сили : поверхневі і об’ємні (масові). Поверхневі сили – це сили, які діють в точках граничної поверхні даної маси рідини. Вони пропорційні розміру площадки , яка взята на цій поверхні

F = P   (4.1)

де F – діюча поверхнева сила, Н ;

 – площа площадки, м2 ;

P = F /  – напруження, Па.

Об’ємні (або масові) сили – це зовнішні сили, які пропорційні об’єму рідини, якщо маса в об’ємі однорідна, тобто густина її однакова по всьому об’єму. Для об’ємних сил справедлива залежність, H

R = j    W, (4.2)

R = j  M,

де W – об’єм рідини, м³ ;

 – густина рідина, кг/м³ ;

j – прискорення, яке надає рідині дана об’ємна сила, м/с² ;

М – маса рідини, кг.

Гідростатичний тиск Р , Па, являє собою напруження стиску в точці, розташованій в середині рідини, яка знаходиться в спокої

, (4.3)

де F – сила тиску рідини на площадку площею  , м², в якій розташована точка, що розглядається.

В даній точці гідростатичний тиск завжди нормальний до площадки, на яку він діє, і не залежить від орієнтації (кута нахилу) площадки. Гідростатичний тиск залежить від положення точки, що розглядається всередині рідини і від зовнішнього тиску, який прикладений до вільної поверхні рідини.

2. Диференційне рівняння рівноваги рідини Ейлера. Основне рівняння гідростатики

В просторі досліджуємо рідини, вибираємо систему координатних вісей x, y, z з центром в точці О і фіксуємо довільну точку А з координатами x, y, z. Потім коло точки А виділимо нескінченно малий паралелепіпед 1-2-3-4-5-6-7-8 з нескінченно малими сторонами dx, dy, dz так, щоб точка А знаходилась в центрі цього паралелепіпеда.

Рисунок 2.1

Гідростатичний тиск, який виникає в точці А під дією зовнішніх сил, позначимо через P.

Виділений паралелепіпед, який знаходиться під дією зовнішніх сил, буде в рівновазі в тому випадку, коли сума проекцій всіх діючих сил на любу із координатних вісей дорівнює нулю.

Установимо зовнішні сили, які діють на досліджує мий нами паралелепіпед. Зовнішніми силами тут являються:

1. об’ємні сили, пропорційні масі паралелепіпеда ;

2. сили гідростатичного тиску, які діють на грані паралелепіпеда зі сторони оточуючої рідини.

Позначимо через X,Y і Z проекції всіх масових сил (сили тяжіння і сили інерції), які віднесені до одиниці маси, на координатні вісі x,y,z. Тоді проекція об’ємних сил dQx на вісь х дорівнює

dQ_x = XdM, ( 1 )

де dM = dx dy dz ρ

Отже

dQ_x = Xdxdydz ρ ( 2 )

Аналогічним шляхом визначаються проекції масових сил на вісі y і z:

dQ_y = Ydxdydz ρ, dQ_z = Zdxdydz ρ ( 2 )

Переходимо до рівнянь сил гідростатичного тиску, які діють на грані паралелепіпеда. Розглянемо сили діючі на вертикальні грані 1-2-3-4 і 5-6-7-8. Згідно першій властивості гідростатичного тиску, ці сили діють нормально до вказаних площадок, тобто направлені вздовж вісі х. Проведемо через точку А горизонтальну лінію ВС, котра перетне грань паралелепіпеда 1-2-3-4 в точці В, а грань 5-6-7-8 в точці С. Гідростатичний тиск в точці В позначимо через PB, а в точці С – через PC. Так як в рідкому середовищі гідростатичний тиск змінюється безперервно по лінійному закону, гідростатичний тиск в точках В і С буде виражатися залежностями

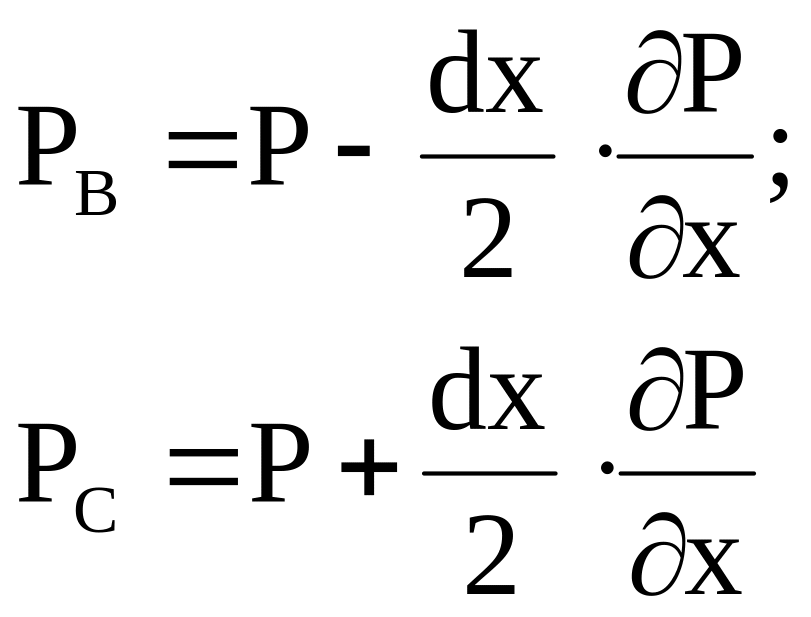( 3 )

де часткова похідна ∂P/∂x називається градієнтом гідростатичного тиску. Площадки 1-2-3-4 і 5-6-7-8 являються нескінченно малими, тому гідростатичні тиски в точках В і С можуть розглядатися як середні гідростатичні тиски для цих площадок. Отже, можна встановити величини сил гідростатичного тиску, які розглядаються:

( 4 )

Проекція на вісь х всіх зовнішніх сил, які діють на паралелепіпед

Р_хВ – Р_хС + dQ_x = 0 ( 5 )

( 6 )

Після нескладних перетворень одержимо

( 7 )

Остаточно

• ∂P / ∂x + ρX = 0

Аналогічним шляхом можна скласти рівняння рівноваги відносно вісей y і z:

- ∂P / ∂y + ρY = 0

- ∂P / ∂z + ρZ = 0

Диференціальні рівняння рівноваги рідини (Ейлера)

( 8 )

Проведемо подальші дослідження. Помножимо кожне із рівнянь відповідно на dx, dy та dz , одержимо

Складемо цю систему рівнянь

(9)

Так як гідростатичний тиск являється функцією тільки координат точки Р=ƒ(x,y,z), то ліва частина рівняння представляє собою повний диференціал тиску

(9а)

Отже

(10)

Так як густина розглянутої нами рідини ρ являється сталою, то рівняння (9,9а) може мати сенс в тому випадку, коли права частина цього рівняння являється повним диференціалом. Для цього необхідно, щоб існувала така функція U=ƒ(x,y,z), часткові похідні котрих по x,y,z дорівнювали б:

∂U/∂x = X; ∂U/∂y = Y; ∂U/∂z = Z ( 11 )

Така функція називається потенціальною, або силовою, а сили, котрі цією функцією виражаються – силами, які мають потенціал.

Отже, рідина може знаходитись в рівновазі тоді, коли система масових сил, діючих на неї, буде мати потенціал. (сили тяжіння, сили інерції)

dP = ρ dU ( 12 )

Основне рівняння гідростатики

dP = ρ dU ( 12 )

(10)

X = 0; Y = 0; Z = -g

dP = - ρg ( 13 )

dP/ρg + dz = 0 ( 14 )

z + P/ρg = C ( 15 )

Граничні умови на поверхні рідини (рис. 2.20) нам відомі: при z = z₀ тиск Р = Р₀

Z₀ + P₀/ρg = C ( 16 )

Рисунок 2.2 – До основного рівняння гідростатики

z + P/ρg = z₀ + P₀/ρg γ = ρg ( 17 )

Остаточно

P = P₀ + ρg ( z₀ – z ) ( 18 )

P = P₀ + ρgh ( 19 )

В найбільш розповсюдженому випадку, коли діє лише сила ваги, гідростатичний тиск Р , Па, в точці, яка знаходиться на глибині h , м , визначається за основним рівнянням гідростатики

Р = Р₀ +   g  h, (15)

де Р₀ – тиск на вільній поверхні рідини, Па ;

 – густина рідини, кг/м³ ;

g – прискорення вільного падіння, м/с² .

З формули (15) витікає, що зовнішній тиск Р₀ , який прикладений до вільної поверхні рідини, передається всім точкам цієї рідини по всім напрямкам однаково (закон Паскаля).

Якщо Р₀ = Р_атм (атмосферний тиск) , то рівняння (15) має вигляд

Р_абс = Р_атм + gh. (16)

Різниця між абсолютним і атмосферним тиском називається надлишковим тиском

Р_над = Р_абс – Р_атм = gh, (17)

звідси h = Р_над / g = (Р_абс – Р_атм) / (g), (18)

де h – п’єзометрична висота (висота тиску).

На глибині в воді h = 10 м надлишковий тиск дорівнює Р_над = 98,1 кПа. Різниця між атмосферним і абсолютним тиском, коли абсолютний тиск менше атмосферного, називається вакуумом

Р_вак = Р_атм – Р_абс =   g  h_вак; (19)

h_вак = (Р_атм – Р_абс) / (  g) = Р_вак / (  g). (20)

Вакуум вимірюється в Па, в кПа, в долях бара або висотою стовпа рідини.

3. Сили сумарного тиску рідини на плоскі поверхні

Сила сумарного тиску. Плоска фігура АВ розташована перпендикулярно до плоскості креслення і похила до горизонту під кутом α.

Рисунок 2.3 – Плоска поверхня, занурена в рідину

Площу фігури позначимо через ω. Така фігура може являтися, наприклад, частиною похилої стінки резервуара або плоским відкидним клапаном, який служить для спорожнювання нафтосховища.

За вісь координат у приймемо лінію, співпадаючу з проекцією фігури АВ на плоскість креслення. Продовжимо цю лінію до перетинання з рівнем вільної поверхні рідини в точці 0. Із точки 0 проведемо вісь 0х, нормальну до направлення АВ. Будемо подумки обертати фігуру АВ навколо вісі 0у так, щоб ця фігура сполучилась з плоскістю креслення. Виділимо на площі фігури нескінченно малу полоску висотою dу, занурену в рідину на глибину h. При цьому відстань полоски від вісі 0x дорівнює у, а площа полоски – d.

Абсолютний гідростатичний тиск в області нескінченно малої полоски може бути прийнятий рівним

Р_абс = Р₀ + h. (16)

Тоді елементарна сила тиску dР , яка приходиться на полоску, визначиться залежністю :

dР_абс = d Р_абс = (Р₀ + h) d. (16)

Розглянемо трикутниr ОМN. Дві сторони його вдомі : МN= h і NО=у . Отже , h= у sin , тоді

dР_абс = Р₀ d = Р₀ + ysin  d.

Для встановлення сили сумарного абсолютного тиску на плоску фігуру АВ проінтегруєм вираз по площі .

.

Інтеграл представляє собою статичний момент площі фігури АВ відносно вісі Ох:

= ω у_с ,

де у_с –відстань центру ваги площі фігури у рідині дв вісі 0х.Тоді

∫ у d = ω h_с ⁄ sin

Остаточно отримаємо :

Р_абс = Р₀  + у sin ω h_с / sin = Р₀  + γω h_с = ω (Р₀ + γ h_с), [Н].

При цьому сила сумарного абсолютного тиску, що діє на плоску фігуру в рідині , виражається добутком площі фігури на величину абсолютного гідростатичного тиску в його центрі ваги. Сила сумарного надлишкового гідростатичного тиску дорівнює вазі стовпа рідини , основою котрого є площа фігури , а висотою – глубина занурювання центру ваги фігури в рідині.

Центр тиску. Відповідно до основного рівняння гідростатики тиск, який діє на поверхню рідини, рівномірно розподіляється по площі фігури, а тому точки прикладення сумарної сили поверхневого тиску Р₀ = Р₀  будуть співпадати з центром ваги фігури.

Сумарна сила надлишкового гідростатичного тиску, навпаки, розподіляється по площі фігури нерівномірно, збільшуючись з глибиною занурювання, і буде лежати нижче центру ваги. Якщо на фігуру з усіх сторін діє атмосферний тиск, що частіше всього спостерігається на практиці, положення центру тиску не залежить від величини сили поверхневого тиску, а тільки від величини надлишкового тиску, який діє на фігуру.

У другому випадку, коли поверхнева сила відміна від атмосферного тиску і діє тільки з однієї сторони фігури, точка прикладення сили сумарного абсолютного гідростатичного тиску буде лежати нижче центру ваги фігури і залежить від положення центру надлишкового тиску. Тому установимо положення центру надлишкового тиску для плоскості АВ.

Із механіки відомо, що момент рівнодіючої сили відносно вибраної вісі дорівнює сумі моментів сил її складових відносно тієї ж вісі. В нашому випадку рівнодіючою є сила сумарного надлишкового гідростатичного тиску

Р= ω γ h_с = ω γ у_с sin,

а складовими силами, із котрих складається сила Р, - сили елементарного надлишкового тиску dР = d ω γ h, які приходяться на нескінченно малі полоски d ω. Складемо вираз для елементарного моменту нескінчена малої сили dР відносно вісі Ох, враховуючи, що h= у sin

dМ = dPy = dω γhy = dω γ y² sinα

Визначимо суму всіх елементарних моментів.

М_с = y² sinα dω = γ sinα = γ sinα І_х.

Інтеграл y² dω = І_х є момент інерції фігури, що розглядається відносно вісі Ох. Момент рівнодіючої сили Р може бути записаний у вигляді:

М_р = Р у_д = ω γ у_д у_с sin α,

де у_д – відстань точки прикладення рівнодіючої Р від вісі Ох , котра являється координатою шуканого нами центру тиску.

Так як М_с = М_р, то γsinαІ_х = ωγу_ду_с sin α , після скорочень І_х = ωу_ду_с, або у_д = І_х / (ωу_с).

Замінимо у формулі момент інерції Іх через центральний момент інерції Іо, тобто через центральний момент інерції фігури відносно вісі , який проходе через її центр ваги.

І_х = І₀ + ω у_с², .