3. Властивості напружень внутрішніх сил в рідині

В становимо зв’язок між напруженнями, які діють на довільно орієнтовану площадку, і три інші взаємно перпендикулярні площадки (рис. 1.2). тобто в рідині, яка рухається, виділемо елементарну рідку частинку у формі тетраедра (рис. 1.2). за мість поверхневих чил на гранях тетраедра показані вектори напружень, які направлені довільним чином до відповідних граней.

Прискорення центра ваги частинки позначимо , напруження масових сил . Запишемо рівняння руху цієї елементарної частинки у векторній формі

, (1.16)

де S_x, S_y, S_z – площі граней тетраедра, які перпендикулярні відповідним вісям координат;

– вектори напружень в центрі площадок, позначення яких відповідає направленню нормалей до них; знаки мінус перед останніми членами означають, що нормалі до відповідних площадок направлені протилежновісям координат.

Із аналітичної геометрії відомо

(1.17)

Розділемо обидві частини (1.16) на S_n і врахуємо (1.17)

. (1.18)

Щоб одержати зв’язок між напруженнями в точці, спрямуємо об’єм тетраедра до нуля, стягуючи його в точку до початку координат. Очевидно, що

, тоді зв’язок між напруженнями буде мати вигляд

. (1.19)

Одержимо, проектуючи на вісі координат

(1.20)

Перший індекс біля проектцій напружень в цих співвідношеннях відповідає площадці, в якій діє дане напруження. Друге – на яку воно проектується. Скалярні величини Р_хх, Р_уу, Р_zz представляють нормальні напруження, а Р_ху, Р_xz … – дотичні напруження, які діють у визначених площадках.

В подальшому будемо позначати дотичні напруження буквою 

(1.21)

враховуючи це, перепишемо (1.20) у вигляді

(1.22)

Н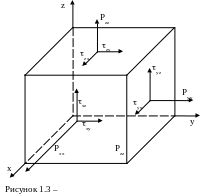 ормалі і дотичні напруження, які діють на три взаємно перпендикулярні грані паралелепіпеда, що виділені в рідині, показані на рис. 1.3

Застосовуючи теорему моментів, які взяті відносно початку координат для напружень, легко довести властивість взаємності дотичних напружень, у відповідності з якими

(1.23)

На основі викладеного можна зробити висновок, що напруження внутрішніх сил в даній точці рідини, тобто напружений стан рідини характеризується сукупністю дев’яти скалярних величин, які утворюють так званий тензор напружень. Внаслідок властивості взаємності (1.23) число незалежних величин в ньому скорочується до шести.

Встановлюємо основні властивості напружень в рідині.

Дотичні напруження , що виникають в рідині, викликані одночасним впливом двох факторів: руху рідини і її в’язкості.

Якщо рідина нерухома, то дотичні напруження в ній відсутні, що характерно як для в’язкої так і для нев’язкої рідини. Таким чином, в рідині, яка в спокої, (в’язкій і нев’язкій) і в нев’язкій рідині, що рухається

(1.24)

Тобто діють лише нормальні напруження Р_хх, Р_уу, Р_zz. Відповідні вектори напружень

. (1.25)

Підставляючи (1.25) в рівняння (1.19), одержимо

. (1.26)

Відомо, що

. (1.27)

Підставим (1.27)в ліву частину (1.26)

(1.28)

Порівнюючи в цьому виразі коефіцієнти при однакових ортах, знайдемо

. (1.29)

або

. (1.30)

Ці рівності дозволяють сформулювати теорему властивостей нормальних напружень: якщо в рідині відсутні дотичні напруження, то нормальні напруження в даній точці не залежать від орієнтації площадки. залежність (1.30) виконується за умови спокою в’язкої рідини і за умови руху і спокою нев’язкої рідини.

Розглянемо одно із основних властивостей рідини, яке пов’язане з нормальними напруженнями. Як видно із рис. 1.3, Р_хх, Р_уу, Р_zz направлені у бік зовнішньої нормалі. Тобто нормальні напруження – напруження розтягу, яким приписується знак плюс. Крапельна рідина, як показує досвід, здатна сприймати довільні зусилля стиснення (від’ємні нормальні напруження) без розриву суцільності. Досвід показує, що рідина практично має розрив при розтягуванні. Тобто, в ній можуть проявлятись лише нормальні зусилля стиснення, які називаються тиском

, (1.31)

величина яких не залежить від орієнтації площадки. Тиск (і взагалі напруження) в системі одиниць МКГСС вимірюють в кГс/м²; його часто вимірюють також у технічних атмосфера (т.а)

.

В системі одиниць СІ тиск прийнято вимірювати в ньютонах на квадратний метр

.

Згідно (1.25)нормальне напруження виражається через тиск залежностями

, (1.32)

де знак мінус вказує, що нормальне напруження в рідині завжди направлено протилежно зовнішній нормалі і є напруженням стиснення.

Тиск в рідині без порушення її суцільності, як показує досвід, не падає нижче тиску Р_н насиченої пари

. (1.33)