2. Диференціальні рівняння руху в’язкої рідини Нав’є-Стокса та елементи теорії подібності й моделювання гідро- газодинамічних явищ

Для отримання рівняння рухув’язкої рідини використаємо загальні рівняння гідродинаміки в напруженнях (3.9)

У цих рівняннях задані проекції напруження масових сил F_z, F_y, F_z та (для нестисливої рідини) густина . Необхідно знайти три проекції швидкості v_z, v_y, v_z , нормальні напруження Р_хх, Р_уу, Р_zz і дотичні напруження. Зважаючи на властивості дотичних напружень Р_ух, = Р_ху, достатньо знайти три дотичні напруження Р_ху, Р_хz та Р_уz. До трьох рівнянь, в які входять дев’ять невідомих величин, додається рівняння суцільності (5.6)

Таким чином система рівнянь (3.9) та (5.6) виходить незамкнутою; у ній число невідомих перевищує число рівнянь. Щоб знайти ці невідомі, необхідно скласти додаткові рівняння, які пов’язують дотичні та нормалні напруження, що виникають в рідині, з її швидкостями.

В’язкість призводить не тільки до виникнення дотичних напружень, але і до зміни нормальних напруженьу порівнянні із випадком нев’язкої рідини.

Припустимо, що нормальне напруження за будь-якою віссю можна уявити у вигляді двох доданків

(8.14)

Перший доданок у цих виразах Р – тис у в’язкій рідині. Другий доданок, який враховує вплив в’язкості, не залежить від тиску. Вважатимемо, що формула Ньютона (8.4), яка отримана для окремого випадку одномірної течії, прийнятна і у загальному випадку тривимірного потоку. Це дозволяє ввести узагальнену гіпотезу Ньютона про те, що напруження, які залежать від в’язкості, пропорційні відповідним відносним швидкостям деформаціїрідкої частинки. При цьому коефіцієнт пропорційності залишається таким самим, як і у формулі (8.4). застосовуючи позначення для відносних швидкостей лінійних і кутових деформацій, запишемо відповідно до цієї гіпотези

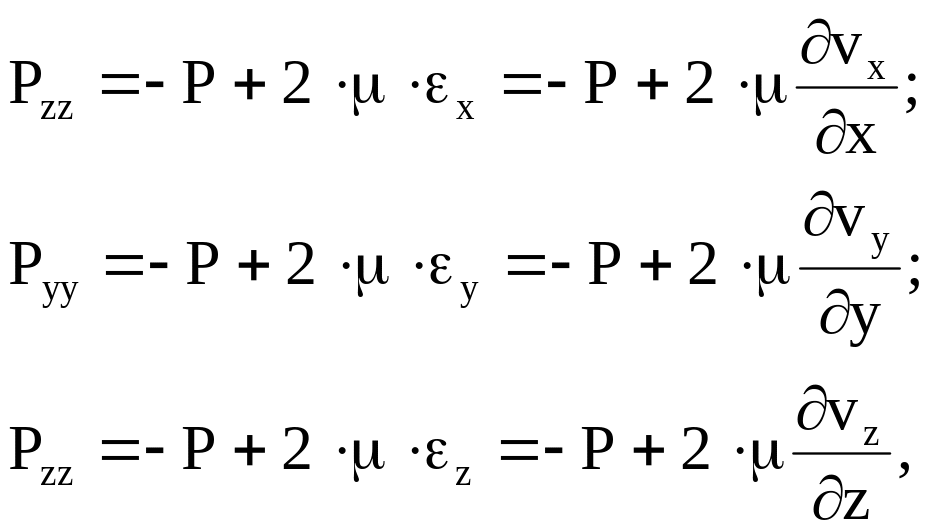(8.15)

де _х, _у, _z – відносні швидкості лінійних деформацій.

Дотичне напруження у відповідності із узагальненою гіпотезою Ньютона

(8.16)

де _х, _у, _z – відносні швидкості кутових деформацій.

Зазначимо, що у пружнього тіла, як витікає із узагальненого закона Гука, напруження пропорційні відповідним відносним деформаціям. У випадку рідини, тобто середовища, яке легко деформується, напруження, за узагальненим законом Ньютона, пропорційні відносним швидкостям деформацій.

Обчислимо середнє арифметичне від величин нормальних напружень за трьома взаємно перпендикулярними напрямками, враховуючи при цьому рівняння суцільності (5.6)

(8.17)

де Р – гідродинамічний тиск.

Із (8.17) виходить, що тиск у в’язкій нестисливій рідині – це взяте із зворотним знаком середнє арифметичне із нормальних напружень за трьома взаємно перпендикулярними напрямками. Знаком мінус у рівнянні (8.17) враховується, що тиск в рідині завжди направлений проти зовнішньої нормалі, тобто, що у ній можуть діяти тільки нормальні напруження, що стискають.

На основі формул (8.15) і (8.16) можна уявити наступну матрицю напруженьу в’язкій рідині, яка визначає, згідно із формулою (_._) її напружений стан

(8.18)

Друга матриця напружень, які залежать від в’язкості, у відповідності до закону Ньютона пов’язана із матрицею відносних швидкостей деформацій залежністю

(8.19)

Для отримання рівняння рухув’язкої рідини підставимо праву частину першого рівняння (3.9) значення нормальних і дотичних напружень відповідно до прийнятих гіпотез (8.15) і (8.16)

(8.20)

де  – оператор Лапласа.

У цьому виразі коефіцієнт  прийнятий сталим, змінено порядок дифернціювання і враховано рівняння суцільності. Похідні від напруженьу другому та третьому рівняннях (3.9) перетворюються аналогічно.

З врахуванням (8.20) отримаємо систему рівнянь руху в’язкої рідини, яка називається рівняннями Нав’є–Стокса

(8.21)

У цій системі повне прискорення в лівій частині виражено через місцеве і конвективне; четверте рівняння, яке замикає систему, є рівнянням суцільності; число невудомих (v_z, v_y, v_z, Р) співпадає із числом рівнянь.

Векторна форма рівнянь Нав’є – Стокса отримуємо множенням скалярних рівнянь (8.21) на орти осей і наступним їх почленним додаванням

(8.22)

Рівняння (8.22) відрізняється від рівняння Ейлера руху нев’язкої рідини членом, який характеризує сили в’язкості, і переходить у нього при  = 0.

Рівняння (8.21) – нелінійне диференційне рівняння другого порядку у часткових похідних. Нелінійність їх обумовлена членом з конвективним прискоренням. Їх рішення слід підкорити початковим та граничним умовам. Усі міркування про початкові умови для течії нев’язкої рідини зберігаються і для в’язкої рідини. Принципово новим є лише зміна граничної умови на твердих межах потоку.

Розглянемо граничну умову на тілі при обтіканні його потоком в’язкої рідини (рис. 8.1). поряд з умової непротікання та безвідривного обтікання (v_n = 0), на поверхні виконується умова прилипання рідини, тобто дотична складова швидкості v_ = 0.

Багаточисленними фізичними вимірювання профіля швидкості біля стінки встановлено, що швидкістьчастинок рідини на стінці прямує до нуля. Найменша відстань від стінки під час цих дослідів складало  0,05 мм. Побічне підтвердження вірності граничної умови прилипання є повне кількісне співпадання багатьох теоретичних рішень, що засновані на цій умові, з дослідними даними. Виконання умови прилипання зовсім не залежить від матеріалу поверхні і ступеня чистоти його обробки. Вона однаково виконуєтьсяпри обтіканні поверхонь як змочуваних так і незмочуваних рідин (як приклад можна навести течію ртуті вздовж скляної струбки). На даний час ця умова є загальноприйнятою у гідромеханіці в’язкої рідини. Вона може порушуватись лише у потоках дуже розріджених газів.

У випадку руху тіла в рідині,яка знаходиться у стані спокою,також виконується умова прилипання. Частинки рідини, що прилягаю до тіла, притягуються ним. На рис. 8.4 зображені епюри швидкості під час руху платини у рідині, яка знаходиться у стані спокою,і при обтіканні пластини потоком рідини.