- •Физикалық шамаларды өлшеулердің нәтижелерін математикалық өңдеу
- •Ілгерілемелі қозғалыстың кинематикасының жӘне динамикасының заңдарын зерттеу
- •2.1 Теориялық кіріспе
- •Максвелл маЯтнигініҢ ҚозҒалысын зерттеу
- •1. Теориялық кіріспе
- •Клеман-Дезорм Әдісімен ауа үшін адиабат көрсеткішін анықтау
- •1. Теориялық кіріспе.
- •2. Тәжірибелік қондырғы.
- •3. Тәжірибені жүргізу.
- •4. Нәтижелерді өңдеу.
- •5. Бақылау сұрақтары
- •1. Теориялық кіріспе.
- •2. Тәжірибелік қондырғы.
- •3. Тәжірибені жүргізу.
- •4. Нәтижелерді өңдеу.
- •5. Бақылау сұрақтары.
- •ЭлектрОстатикалыҚ Өрісті зерттеу
- •1. Теориялық кіріспе
- •1) Электр өрісінің кернеулігіөрісті күш жағынан сипаттайды;
- •2) Электр өрісінің потенциалы − өрісті энергетикалық тұрғыдан сипаттайды.
- •2. Эксперименттік қондырғы
- •3. Тәжірибені орындау реті және өлшеу нәтижелерін өңдеу.
- •4. Бақылау сұрақтары
- •Омның жалпылама заңы
- •1. Теориялық кіріспе
- •2. Эксперименттік қондырғы
- •Бақылау сұрақтары.
- •Тұрақты ток тізбегіндегі пайдалы қуаттың жүктеменің кедергісіне тәуелділігін зерттеу
- •1. Теориялық кіріспе
- •2. Эксперименттік қондырғы
- •4. Бақылау сұрақтары
- •Математикалық маятниктің кӨмегімен
- •1. Теориялық кіріспе
- •2. Жұмыстың орындалуы
- •3. Жұмыстың орындалу тәртібі
- •4. Бақылау сұрақтары
№ 1.ЗЕРТХАНАЛЫҚ ЖҰМЫС
Физикалық шамаларды өлшеулердің нәтижелерін математикалық өңдеу
Жұмыстың мақсаты: тәжірибелердің нәтижелерін өңдеудің әдістерімен танысу, өлшенетін шамаларды сенім аралықтары арқылы бағалау.
1.1 Теориялық кіріспе
Физикалық тәжірибелерді жүргізу, әрқашанда физикалық шамаларды өлшеулермен байланысты. Өлшеудің екі түрі бар: зерттелетін физикалық шама тікелей өлшенетін болса, ол тікелей өлшеу деп аталады. Ал ізделініп отырған физикалық шаманың мәні тікелей өлшеулерге тәуелді белгілі заңдылықтар арқылы табылса, ол жанама өлшеу деп аталады.
Қандай болса да жүргізілген өлшеулерді қаншама мұқият орындасақ та, ол қатесіз болмайтындығын тәжірибелер көрсетіп отыр, біз тек жуық мәнге ғана ие боламыз.
Өлшеулердің барлық мүмкін қателіктерінің пайда болу сипаттарын екі түрге бөлуге болады. Жүйелік қателіктердің пайда болу себебі - өлшеуші қондырғылар мен аспаптардың аса жетілдірілмегендігінен, тәжірибенің жүру жағдайларының ерекшелігімен және өлшеу әдісінің кемістігнен пайда болады. Сондықтан системалық қателік тәжірибені жүргізгенде шарт өзгермесе, олар таңба жағынан да, шама жағынан да тұрақты (систематикалық қайталанады) болып қала береді. Мұндай қателіктерді қондырғыларды салыстырып тексеру арқылы ескеруге және өлшеу әдістерін жетілдіру арқылы кемітуге болады
Кездейсоқ қателіктер әрқашанда тәжірибелерде болады және ол көптеген кездейсоқ бақыланбайтын кедергілердің жиынтығының қосындысынан тұрады. Олар құрал-жабдықтардың дәлдіктерінің шектеулі екендігімен байланысты, біздің сезуші ағзаларымыздың мүмкіндіктерінің шектілігімен, сыртқы ортаның өзгеру жағдайларымен т.с.с. байланысты болады. Мұндай қателіктерді болдырмау мүмкін емес, бірақ олар ықтималдық теория заңдылығына бағынатындықтан, өлшеу санын жеткілікті көп рет өлшеу арқылы шын мәннің болатын шектің арасын көрсетуге болады.
Кездейсоқ қателіктің тағы бір түрі мылт кету. Бұл тәжірибешінің ұқыпсыздығынан алынған нәтиже. Көп жағдайда бірнеше рет өлшеулерден кейін бұл қателік ерекше бөлініп тұрады. Нәтижелерді өңдеген кезде оларды ескермей, есептеуден шығарып тастау керек.
Егер физикалық шама х бірнеше рет (n рет) қайталанып өлшенетін болса, оның шын мәніне (хшын) жүргізілген өлшеулер нәтижелерінің орташа арифметикалық ықтималдық мәні жақын болады.
1.1.1 Тікелей өлшеулердің нәтижелерін өңдеу реті
Егер
қандай да бір физикалық шамаларды
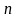 рет өлшейтін болсақ, онда оның шын
мәнінің
рет өлшейтін болсақ, онда оның шын
мәнінің
 ықтимал шамасы, жүргізілген өлшеулердің
орташа арифметикалық мәніне жақындайды:
ықтимал шамасы, жүргізілген өлшеулердің
орташа арифметикалық мәніне жақындайды:
 , (1.1)
, (1.1)
мұндағы
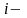 ші
өлшеудің нәтижесі.
ші
өлшеудің нәтижесі.
Өлшеулер
көп рет қайталанып (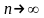 )
жүргізілген болса, орташа
)
жүргізілген болса, орташа
 шамасы
мәніне ұмтылады. Әрбір
шамасы
мәніне ұмтылады. Әрбір
 мәні орташа
мәнінен кездейсоқ ауытқиды. Жеке
өлшеулердің қателігіне
мәні орташа
мәнінен кездейсоқ ауытқиды. Жеке
өлшеулердің қателігіне
 . (1.2)
. (1.2)
айырым қабылданған.
Бұл
 қателік теріс те, оң да бола алады. Өлшеу
қателіктерінің модулдерінің орташа
арифметикалық шамасы бірінші жуықтауда
өлшеу нәтижелерінің абсолют қателігін
қателік теріс те, оң да бола алады. Өлшеу
қателіктерінің модулдерінің орташа
арифметикалық шамасы бірінші жуықтауда
өлшеу нәтижелерінің абсолют қателігін
 береді
береді

 .
(1.3)
.
(1.3)
Өлшенетін шаманың шын мәні сенім аралығы деп аталатын мәндер аралығының ішінен табылады:
 . (1.4)
. (1.4)
Сенім
ықтималдығы немесе сенімдік коэффициент
 өлшеу нәтижесі шын мәннің шамасынан
өзгешелігі
шамасынан аспайтындығының Р ықтималдығын
көрсететін шама
өлшеу нәтижесі шын мәннің шамасынан
өзгешелігі
шамасынан аспайтындығының Р ықтималдығын
көрсететін шама
 . (1.5)
. (1.5)
Гаусстың кездейсоқ қателіктер теориясының көмегімен шамасын дәлірек анықтауға болады және бұдан басқа өлшеу нәтижелерінің (1.4) аралыққа енетін үлесін көрсетуге болады.
Егер кездейсоқ қателік үлкен болмаса және қалыпты заң бойынша таралуы орындалса, яғни Гаусс функциясымен сипатталатын болса,
 , (1.6)
, (1.6)
онда абсолюттік қателік пен және сенім ықтималдығының арасында анық байланыс болады.
(1.6)
формуладағы
 орташа арифметикалық шаманың орташа
квадраттық қателігі немесе стандарттық
ауытқу деп аталады. Өлшеудің шекті
санында
ол төмендегі формуламен бағаланады
орташа арифметикалық шаманың орташа
квадраттық қателігі немесе стандарттық
ауытқу деп аталады. Өлшеудің шекті
санында
ол төмендегі формуламен бағаланады
 =
= . (1.7)
. (1.7)
Өлшеулерді
көп рет (
)
қайталап жүргізетін болсақ, есептеулер,
өлшеудің нәтижелері шын мәнінің шамасынан
өзгешелігі
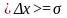 шамадан артпайтындығының ықтималдығы
0,68-ге тең екендігін көрсетеді, яғни
шамадан артпайтындығының ықтималдығы
0,68-ге тең екендігін көрсетеді, яғни
 ,
,
ал 2 үшін және 3 үшін жазсақ,
 ,
(1.8)
,
(1.8)
 .
.
Өлшеулердің
саны азайған болса, онда нанымдылығы
азаяды және сол бір сенімділік ықтималдылық
үшін сенімділік аралығын
 есе
арттыруымыз керек.
есе
арттыруымыз керек.
 . (1.9)
. (1.9)
мұндағы - Стъюдент коэффициенттері деп аталады, ол ықтималдылық теориясымен есептеп шығарылады. Әртүрлі сенім ықтималдылығы және өлшеу саны n үшін мәні 1.1-кестеде келтірілген.
1.1-кесте
|
|
|||||||
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,96 |
0,99 |
|
2 |
1,00 |
1,58 |
2,0 |
3,1 |
6,3 |
12,7 |
31,3 |
63,6 |
3 |
0,82 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
31,6 |
4 |
0,77 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,6 |
12,9 |
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
8,6 |
6 |
0,73 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
6,9 |
7 |
0,72 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
6,0 |
8 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
5,4 |
9 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
5,0 |
10 |
0,70 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
2,8 |
4,3 |
15 |
0,69 |
0,87 |
1,1 |
1,3 |
1,8 |
2,1 |
2,6 |
4,1 |
20 |
0,69 |
0,86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
3,9 |
40 |
0,68 |
0,85 |
1,1 |
1,3 |
1,7 |
2,0 |
2,4 |
3,6 |
60 |
0,68 |
0,85 |
1,0 |
1,3 |
1,7 |
2,0 |
2,4 |
3,6 |
120 |
0,68 |
0,85 |
1,0 |
1,3 |
1,7 |
2,0 |
2,4 |
3,4 |
Өлшеулер нәтижелерінің дәлдігі салыстырмалы қателікпен сипатталады, ол
 , (1.10)
, (1.10)
абсолют қателік өлшенген шаманың қандай үлесін құрайтындығын көрсетеді. Бұдан басқа салыстырмалы қателіктің шамасына қарап әртекті физикалық шамалардың өлшену дәлдігін салыстыруға болады.
Кез
келген физикалық шаманы өлшеу берілген
сенімділік ықтималдығымен
сенім аралығымен
 және салыстырмалы қателіктің
және салыстырмалы қателіктің
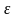 көрсетілуімен аяқталуы керек.
көрсетілуімен аяқталуы керек.
Соңғы нәтиже
 . (1.11)
. (1.11)
түрде жазылуы керек.
Мысалы,
 .
.
Өлшеудің қателіктерінің нәтижесін жазғанда екі мәнді санға дейін немесе қателіктің алғашқы мәнді сандары үштен көп болса, онда бір мәнді санға дейін дөңгелектеу керек. Абсолют қателік дегеніміз нәтиженің қандай разрядында дәлдік орын алмай тұрғанын көрсетеді, олай болса нәтижені қателіктің табылған мәнді санына дейінгі разрядқа дейін дөңгелектеу қажет.
Мысалыға: немесе
немесе
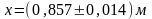 .
.
1.1.2 Жанама өлшеулердің нәтижелерін өңдеу реті
Ізделініп отырған физикалық шаманың мәнін табу тікелей өлшенетін шамаға және басқа да шамаларға тәуелділігінің негізінде жиі қолданылады.
Өлшеу
қателігі, өлшенетін шамадан әдетте көп
кіші болатындықтан дифференциалдық
есептеулерді қолдануға болады. Бұл үшін
дифференциалдың белгісін d
қателіктің белгісімен
 ауыстыруға болады.
ауыстыруға болады.
Ізделінетін шама у өлшенетін шамамен х функционалдық тәуелдікте болсын
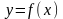 . (1.12)
. (1.12)
Шаманы тіке өлшеудегі dх қателік іздеп отырған шамада dу қателіктің пайда болуын тудырады
 . (1.13)
. (1.13)
Оң жағын Тейлор қатарына жіктеп және бұл қатардың тек екі мүшесімен шектелсек, онда
 . (1.14)
. (1.14)
 және
және
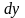 дифференциалдарды
дифференциалдарды
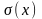 және
және
 орташа квадраттық қателікке ауыстырсақ,
алатынымыз
орташа квадраттық қателікке ауыстырсақ,
алатынымыз
 , (1.15)
, (1.15)
яғни
функциясының абсолют қателігі осы
функцияның туындысын
 аргументтің
абсолют қателігіне көбейткенге тең.
аргументтің
абсолют қателігіне көбейткенге тең.
Функцияның салыстырмалы қателігі
 , (1.16)
, (1.16)
өрнегімен анықталады, яғни осы функцияның натурал логарифмінің дифференциалына тең.
Жалпы жағдайда, егер ізделініп отырған шама у тәжірибеде тікелей өлшенетін бірнеше айнымалылардың хі функциясы болса, онда
 , (1.17)
, (1.17)
абсолют қателік
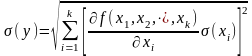 =
= , (1.18)
, (1.18)
өрнегімен
анықталады. Мұндағы
 - айнымалы
бойынша (1.17) функциясының дербес туындысы,
ал қалған айнымалылардың бәрі тұрақтылар
деп есептеледі.
- айнымалы
бойынша (1.17) функциясының дербес туындысы,
ал қалған айнымалылардың бәрі тұрақтылар
деп есептеледі.
Егер у үшін өрнекте шамасы көбейтінді түрде енетін болса (оң немесе теріс дәрежелерде), онда бірінші салыстырмалы қателікті табу ыңғайлы болады.
 , (1.19)
, (1.19)
Осыдан кейін берілген ықтималдығымен сенім аралығын жазу керек
 . (1.20)
. (1.20)
1.2 Жұмыстың орындалуы
Жабдықтар мен қажеттілер: дөңгелек пішінді цилиндр, таразы, штангенциркуль.
1.2.1 1-жаттығу. Тікелей өлшеудің нәтижесін өңдеу.
Бұл шариктің диаметрін микрометрмен өлшеу болуы мүмкін, Гейгер санағышының көмегімен космостық сәулелердің интенсивтілігін тіркеу, рычагты таразымен денелердің массасын өлшеп анықтау, заттардың ұзындығын штангенциркульмен өлшеу т.с.с. Көрнекті болуы үшін дененің массасын өлшеудің нәтижелерін өңдеу 1.2-кестеде келтірілген.
1.2-кесте
|
|
|
|
|
|
|
|
|
% |
1 |
18,4 |
18,42 |
0,02 |
0,22 |
0,0004 |
0,084 |
|
0,2 |
1,1 |
2 |
18,7 |
0,28 |
0,0784 |
||||||
3 |
18,2 |
0,22 |
0,0484 |
||||||
4 |
18,6 |
0,18 |
0,0324 |
||||||
5 |
18,5 |
0,08 |
0,0064 |
||||||
6 |
18,3 |
0,12 |
0,0144 |
||||||
7 |
18,0 |
0,42 |
0,1764 |
||||||
8 |
18,1 |
0,32 |
0,1024 |
||||||
9 |
18,8 |
0,38 |
0,1444 |
||||||
10 |
18,6 |
0,18 |
0,0324 |
||||||
|
|
|
2,2 |
|
0,636 |
|
|
|
|
Оқытушының ұсынысымен, басқа физикалық шамаларды тікелей өлшеп өңдеудің нәтижелерін 1.3-кестені толтырыңыз.
1) Қалаған физикалық шаманы n рет өлшеп, мәндерді 1.3-кестеге енгізіңіз.
2) Ең ықтимал мәнді (1.1) формула бойынша анықтаңыз:

3)
Әрбір
өлшеулердің орташа мәнінен ауытқуының
модулін
 (1.2)
формула бойынша анықтаңыз, нәтижені
1.3-кестеген енгізіңіз.
(1.2)
формула бойынша анықтаңыз, нәтижені
1.3-кестеген енгізіңіз.
4)
Орташа
арифметикалық
 ауытқуды (1.3)
формуламен табыңыз.
ауытқуды (1.3)
формуламен табыңыз.
5)
Өлшеулердің
нәтижелерінің орташа квадраттық қатесін
 (1.7) формуладан
анықтаңыз.
(1.7) формуладан
анықтаңыз.
6) Оқытушы ықтималдық үшін көрсеткен өлшем саны n бойынша, Стъюдент коэффициентін дайын кестеден табыңыз.
7) Сенім аралығын (өлшеу қателігі) (1.9) формула бойынша табыңыз.
8) Өлшеудің салыстырмалы қателігін (1.10) формуламен есептеңіз.
9) Соңғы нәтижені (1.11) түрінде жазыңыз.
1.3-кесте
|
, |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
3 |
|
|
|
||||||
4 |
|
|
|
||||||
5 |
|
|
|
||||||
6 |
|
|
|
||||||
7 |
|
|
|
||||||
8 |
|
|
|
||||||
9 |
|
|
|
||||||
10 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1.2.2 2-жаттығу. Жанама өлшеулердің нәтижелерін өңдеу.
Бұл дененің жылдамдығын есептегенде жол ұзындығын, қозғалыстың уақытын өлшеу нәтижесінде болуы мүмкін, дененің массасы мен көлемін өлшеп, тығыздықты тапқанда, өткізгіштердің кедергісі мен өлшемдерін өлшеу нәтижесінде меншікті кедергіні тапқанда т.с.с. Көрнекті болу үшін (1.4 –1.6 кестелерде) заттың тығыздығын табудағы жанама жолдың нәтижелерін өңдеуі берілген.
1) Цилиндрдің массасын m, биіктігін h және диаметрін d әрқайсысын 5 реттен өлшеңіз. Нәтижесін 1.4, 1.5 және 1.6 кестеге енгізіңіз.
2)
Жазылған (1.1) формуламен ең ықтимал
массаны
,
биіктікті
 және диаметрін
және диаметрін
 анықтаңыз.
анықтаңыз.
3)
Өлшеулердің нәтижелерінің орташа
квадраттық қателерін
,
 және
және
 (1.7) формула бойынша анықтаңыз.
(1.7) формула бойынша анықтаңыз.
1.4 –кесте
|
|
|
|
, |
|
1 |
95,8 |
95,52 |
0,28 |
0,0784 |
0,107 |
2 |
95,2 |
0,32 |
0,1024 |
||
3 |
95,5 |
0,02 |
0,0004 |
||
4 |
95,7 |
0,18 |
0,0324 |
||
5 |
95,4 |
0,12 |
0,0144 |
||
|
477,6 |
|
0,228 |
|
1.5-кесте
|
|
|
|
|
|
1 |
50,3 |
50,12 |
0,18 |
0,0324 |
0,058 |
2 |
50,0 |
0,12 |
0,0144 |
||
3 |
50,1 |
0,02 |
0,0004 |
||
4 |
50,2 |
0,08 |
0,0064 |
||
5 |
50,0 |
0,12 |
0,0144 |
||
|
250,6 |
|
|
0,068 |
|
1.6-кесте
|
|
|
|
|
|
1 |
30,7 |
30,7 |
0 |
0 |
0,044 |
2 |
30,8 |
0,1 |
0,01 |
||
3 |
30,6 |
0,1 |
0,01 |
||
4 |
30,6 |
0,1 |
0,01 |
||
5 |
30,8 |
0,1 |
0,01 |
||
|
153,5 |
|
0,04 |
|
4) Тығыздықтың ең ықтимал мәнін

формуласы бойынша анықтаңыз.
5 )
Тығыздықтың салыстырмалы қателігін
(1.19) формуламен есептеңіз:
)
Тығыздықтың салыстырмалы қателігін
(1.19) формуламен есептеңіз:
6) Тығыздықтың орташа квадраттық қателігін (1.16) формуламен есептеңіз:
 ;
;
7) Стъюдент кестесі бойынша оқытушының көрсеткен ықтималдығы үшін коэффициентінің мәнін n өлшеу саны бойынша табыңыз:
мысалыға,
 ;
;
8)
Сенім аралығын
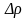 (өлшеу қателігін) (1.9) формула бойынша
табыңыз.
(өлшеу қателігін) (1.9) формула бойынша
табыңыз.
 ;
;
9) Соңғы ақтық нәтижелерді (1.12) түрде жазыңыз.
 .
.
1.3 Бақылау сұрақтары
1. Тікелей және жанама өлшеулер, жүйелік және кездейсоқ қателіктер.
2. Абсолют және салыстырмалы қателіктер.
3. Сенім аралықтары және сенім ықтималдықтары.
4. Тікелей және жанама өлшеулердің нәтижелерін өңдеу.
№ 2.ЗЕРТХАНАЛЫҚ ЖҰМЫС

 ,
,

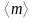 ,
,
 ,
, ,
,
 ,
,




 184,2
184,2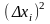

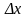
 ,
,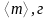


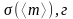

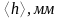

 ,
,
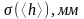
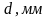
 ,
, ,
, ,
,