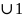1. hipotezę h0 należy przyjąć

2. Nie ma podstaw do odrzucenia hipotezy h0

3. hipotezę h0 należy odrzucić

4. hipotezę h1 należy odrzucić

13. Zmienna losowa X ma rozkład normalny z parametrami m i σ. Aby zweryfikować hipotezę H0:m=15 wobec hipotezy alternatywnej H1:m<15 obliczono wartość odpowiedniej statystyki testu na podstawie próby losowej otrzymując u=2,32. Obszar krytyczny ma postać U=-3,06. Zatem na przyjętym poziomie istotności:

a) hipotezę H0 należy przyjąć

b) nie ma podstaw do odrzucenia hipotezy H0

c) hipotezę H0 należy odrzucić

d) hipotezę H1 należy odrzucić

14. Suma prawdopodobieństw w funkcji prawdopodobieństwa zmiennej losowej wynosi:

1. -1

2. 0

3. µ

4. 1

15. Zmienna losowa X jest:

1. funkcją określoną na zbiorze zdarzeń elementarnych

2. przyjmuje wartości z przedziału [0, 1]

3. jest funkcją określoną na zbiorze liczb rzeczywistych

4. nie może przyjąć wartości 2

3. Zmienna losowa X podlega rozkładowi normalnemu z wartością średnią 55 i odchyleniem standardowym 5. Zatem:

a) P(X>55)=0

b) P(X <55)= 0,5

c) P(X=55)>0

d) P(X≤55)<0,5

16. Aby zweryfikować hipotezę statystyczną o przeciętnej liczbie wypalanych papierosów w populacji studentów należy zastosować test:

1. dla średniej

2. dla wskaźnika struktury

3. nieparametryczny , współczynnika korelacji

4. dla wariancji

17. Aby zweryfikować hipotezę statystyczną o zróżnicowaniu liczby wypalanych papierosów w populacji studentów należy zastosować test istotności:

1. dla średniej

2. dla wskaźnika struktury

3. nieparametryczny

4. dla wariancji

18. Aby zweryfikować hipotezę statystyczną głoszącą, że więcej niż połowa studentów pali papierosy należy zastosować test :

5. dla średniej

6. dla wskaźnika struktury

7. nieparametryczny

8. dla wariancji

17. Aby zweryfikować hipotezę czy rozkład wagi osób jest zgodny z rozkładem normalnym można zastosować test:

a) zgodności

b) niezależności

c) spójności

d) efektywności

4. Typowy poziom istotności przyjmowany we wnioskowaniu statystycznym wynosi:

a )0,05

b) 0,90

c) 0,01

d) 0,95

1. Zmienna losowa X ma rozkład normalny z parametrami  i σ lub (m i σ). Poprawę precyzji estymacji przedziałowej parametru  można uzyskać przez:

a) zmniejszenie liczebności próby

b) zwiększenie współczynnika ufności

c) zwiększenie liczebności próby

d) zwiększenie szerokości przedziału ufności

5. O zdarzeniach A i B wiadomo, że A∩B =∅. Są to więc zdarzenia:

a)pewne

b)zależne

c)niezależne

d)wykluczające się

19. Jeżeli zmienna losowa ma rozkład normalny N(10,5), to:

1. P(X<5)=-0,5

2. P(X=5)=0,5

3. P(X>10)=0,5

4. E(X)=10 oraz D²(X)=100

20. Współczynnik ufności wynosi 97%, a więc:

1. wiarygodność przedziału wynosi 97%

2. przedział ufności zawiera 0,97 nieznanej wartości parametru

3. alfa=0,97 [jeśli już to „1-alfa”]

4. długość przedziału ufności wynosi 0,97

10. Rozkładem właściwym do wyrażenia prawdopodobieństwa liczby katastrofalnych uderzeń dużych ciał niebieskich w Ziemię jest rozkład:

a) Poissona

b) Bernoulliego

c) normalny

d) prostokątny

21. Poziom istotności alfa to inaczej:

1. prawdopodobieństwo odrzucenia błędu pierwszego rodzaju

2. prawdopodobieństwo odrzucenia fałszywej hipotezy zerowej

3. prawdopodobieństwo błędu drugiego rodzaju

4. prawdopodobieństwo przyjęcia fałszywej hipotezy zerowej

co sprawdza test wariacji średnich arytmetycznych? - równość średnich arytmetycznych

"Czy współczynnik korelacji 0,3 może być silniejszy niż 0,6?" - może,jeśli liczyć od większej liczby

Nie r => 1 do 0,7 silna; 0,6-0,4 umiarkowana; 0,3 do 0 słaba.

"Którą zmienną wybieramy do wyrzucenia?"- należy eliminować po jednym x wybierając do wyrzucenia ten,który ma największe P

"Kiedy odrzucamy H0?" Wtedy, gdy wartość wyznaczona empirycznie (u emp; t emp; chi emp) zawiera się w przedziale wartości krytycznej (tak to byłoby po statystycznemu?)

kiedy p<alfa

Który z elementów jest losowy, a który nie? - estymator losowy. (ocena/wynik-nielosowy parametr-nielosowy )

Co sprawdza test analizy wariancji? - średnia arytmetyczna

Co sprawdza analiza wariancji? – równość średnich arytmetycznych

metoda najmniejszych kwadratów

standardowa metoda przybliżania rozwiązań układów nadokreślonych, tzn. zestawu równań, w którym jest ich więcej niż zmiennych. Nazwa „najmniejsze kwadraty” oznacza, że końcowe rozwiązanie tą metodą minimalizuje sumę kwadratów błędów przy rozwiązywaniu każdego z równań.

Identyfikacja skali pomiaru

http://pedagogikaspecjalna.tripod.com/notes/pdscales.html

16. Ujemną wartość może osiągnąć:

a) dystrybuanta (не це точно)

b) prawdopodobieństwo

c) zmienna losowa

d) wariancja

16. Ujemną wartość może osiągnąć:

a) dystrybuanta

b) dla wskaźnika struktury

c) nieparametryczny

d) dla wariancji

12. Pożądaną własnością estymatora parametru populacji jest:

a) spójność

b) zwrotność

c) przechodniość

d) zgodność

9. Chcąc zweryfikować hipotezę o odsetku osób zarabiających więcej niż średnia należy zastosować test dla:

a) wariancji

b) średniej

c) frakcji

d) odchylenia standardowego

7. Statystyka testu dla wariancji przy prawdziwości H0 w małej próbie ma rozkład:

a) równomierny

b) chi-kwadrat

c) t-Studenta

d)F-Snedecora

4. Statystyka testu dla dwóch wariancji przy założeniu prawdziwości H0 ma rozkład:

a) normalny

b) Poissona

c) t-Studenta

d) F-Snedecora

5. Postulatu (?) małej wariancji estymatora dotyczy własność:

a) zwrotności

b) zgodności

c) spójności

d) efektywności

1. Kolor oczu to przykład cechy mierzonej w skali

a) nominalnej (wyróżnia jednostki ze względu na fakt posiadania lub nieposiadania danej cechy, nie da się wartościować np. płeć, grupa krwi)

b) porządkowej (pozwala ułożyć jednostki w kolejności, rangowanie, np. cena wysoka/niska)

c) przedziałowej (pozwala określić nie do końca dokładne różnice między jednostkami np. temperatura)

d) ilorazowej (ma zastosowanie wyłącznie do cech ilościowych (nie jakościowych) dokładne różnice, ,np.zysk przedsiębiorstwa, liczba zatrudnionych)

e) iloczynowej (chyba takiej nie ma ;D)

11. Błąd I rodzaju - odrzucenie hipotezy prawdziwej

błąd II rodzaju - przyjęcie hipotezy fałszywej

8. Czym są błędy pierwszego i drugiego rodzaju?

pierwszy - odrzucenie hipotezy prawdziwej, drugi przyjęcie hipotezy błędnej

1 .Z jakiego przedziału wartości przyjmuje współczynnik korelacji liniowej?

Przyjmuje wartości z przedziału [-1, +1]

2. Interpretacja wartości p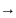

Powinno być mniejsze od poziomu istotności alfa, wtedy należy odrzucić hipotezę zerową H₀ na rzecz hipotezy alternatywnej H_1­­.

4. Która miara działa w ten sposób że im więcej tym lepiej ?

Współczynnik determinacji R² à jest to miara niemianowana, ale czasem bywa wyrażana w procentach

5.Ile parametrów decyduje w rozkładzie normalnym = 2 (lub 3, na pewno sigma)

6. Ile parametrów decyduje w rozkładzie wykładniczym = 1 (lambda)

7. Ile może być najmniej serii odchyleń (kryteria dobroci dopasowania)? - > 3

9. Skąd się bierze alfa? odp. sami ją przyjmujemy lecz: R.A. FISHER przyjmuje że alfa to 0.05A. SOKOŁOWSKI że alfa to 0.10

10. Prawdopodobieństwo należy do przedziału: 0≤P(A)≤1

x1, x2- rangi -to miary wtedy: Współczynnik Spearman’a, Kendall

11. Które z podanych zmiennych jest zmienną losową?

ESTYMATOR

12. Ile wynosi wartość dla rozkładu normalnego α = 0,95?

1,960

13. Czy odchylenie standardowe może być większe od wariancji? TAK, nie sądzę

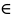s> , gdy s 0