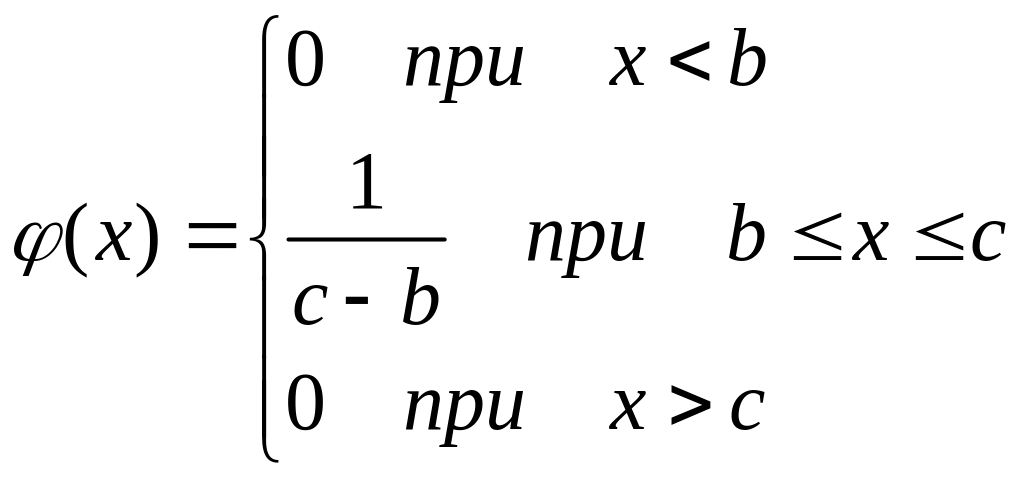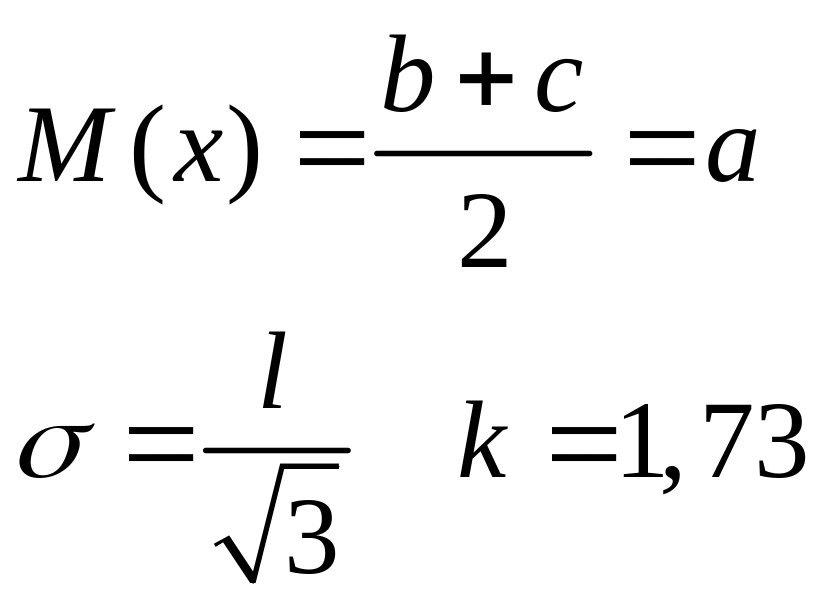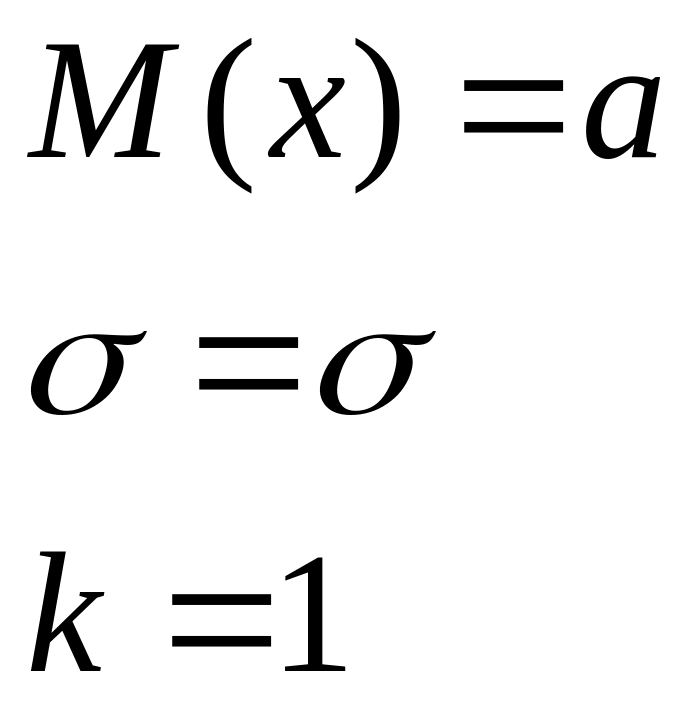3.2. Объем выборки

1. При известной :

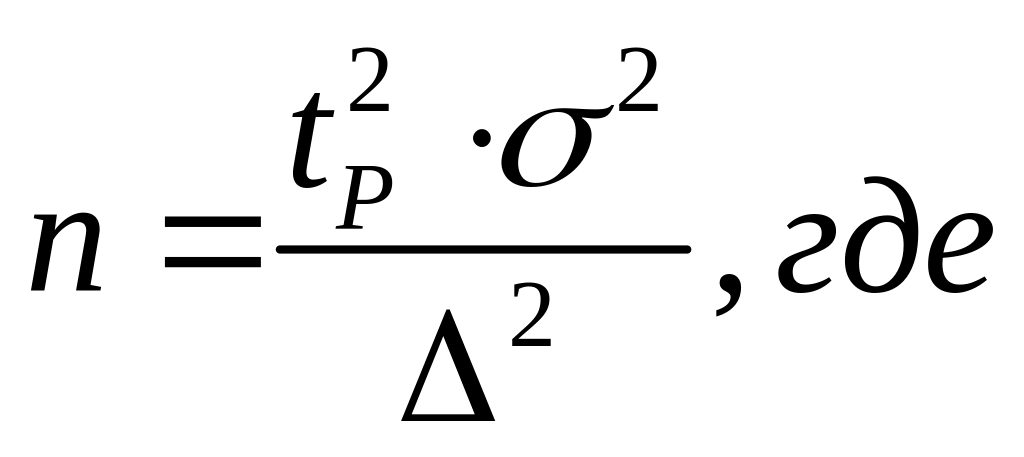
- допустимая погрешность определения среднего.

- среднее квадратичное отклонение.

- квантиль нормального распределения.

При , .

2. При неизвестной :

(при ), где - выборочная дисперсия.

(при ), где - квантиль распределения Стьюдента.

Если не задано, то производят предварительную выборку с , по результатам измерения которого определяют S.

Пример: При обработке деталей произошло смещение центра группирования размера. Рассчитать объем выборки, необходимый для определения среднего значения с точностью при .

Допуск - 0.21 (мм). Ориентировочное значение : .

Рассчитываем объем выборки: .

Часто встречающиеся законы распределения

закон распределения	эскиз	Плотность вероятности	характеристика
Равной вероятности
Симсона
Гаусса нормальный
Релея
Модуля разности			k зависит от соотношения и

k – коэффициент относительного рассеивания

Закон равной вероятности встречается при ошибках округления по шкале , ошибках от воздействия фактора, изменяющегося по линейному закону, например, износа инструмента.

Закон Симпсона встречается при сложении двух случайных величин, распределенных по закону равной вероятности, например, отсчёт по шкале не от нуля.

Закон Гаусса(нормальный закон)

По центральной предельной теореме Ляпунова : если случайная величина состоит из суммы случайных величин и не одна из них не доминирует, то суммарная величина распределена по нормальному закону.

Закон Релея (закон экцентриситета): если величины аспределены по нормальному закону, то величина распределена по закону Релея.

Модуль разности: если величины распределены по нормальному закону, то величина распределена по закону модуля разности. По этому закону распределены погрешности формы и расположения: - отклонения от параллельности , отклонение от перпендикулярности , конусность, овальность и т.д.

Интегральные функции. Функция Лапласа. Определение процента брака.

Для определения процента годных и негодных изделий необходимо определить вероятность попадания значения в заданный интервал.

Вероятность того, что случайная величина меньше x равна заштрихованной площади под кривой (Рис.3).

Рис. 3 Определение годной и негодной продукции.

Площадь под кривой равна интегралу от плотности вероятности или интегральной функции.

Интегральная функция или функция распределения F(x) равна вероятности того, что в результате опыта случайная величина приняла значение меньше x.

F(x)=P(ξ<x)

Рис.4 Функция распределения или интегральная функция.

Для вычисления интеграла часто пользуются функцией Лапласа. Для этого делается замена переменной x на t по нижеприведенным формулам, а функция Лапласа Ф(t) табулируется.

Замечание: функция распределения F(x) имеет пределы интегрирование от минус бесконечности до x, а функция Лапласа Ф(t) – от 0 до t.

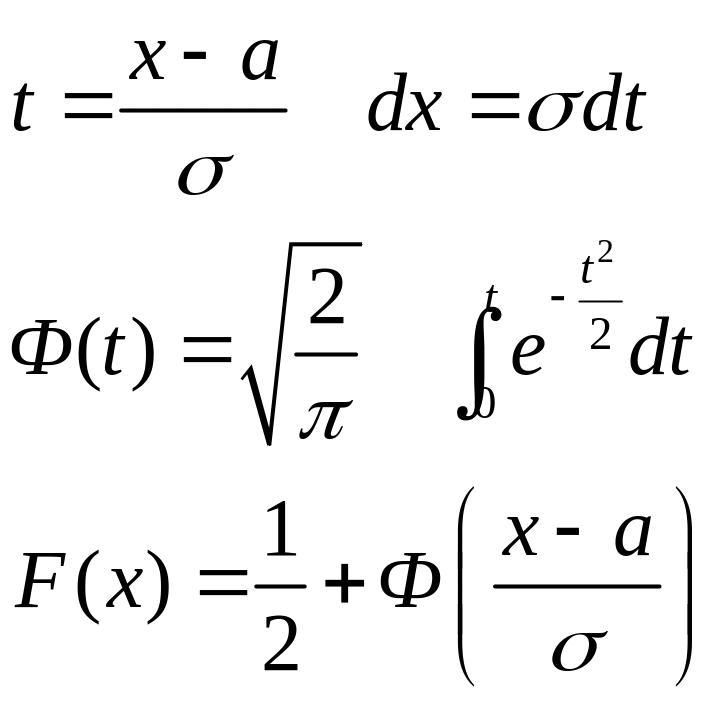
Для определения процента брака в Mathcad используют интегральную функцию pnorm. где μ – математическое ожидание, σ – среднеквадратичное отклонение, x – предельное значение случайной величины.

Например, найти процент бракованных заготовок диаметром 20_-1.

Для определения процента брака необходимо найти максимальный предельный диаметр d_max, минимальный предельный диаметр d_min, среднее значение μ и среднеквадратическое отклонение σ.

d_max=d+es, d_min=d+ei где d – номинальный диаметр, es – верхнее предельное отклонение, ei – нижнее предельное отклонение.

d_max=20+0=20, d_min=20+(-1)=19

Среднее значение элементов массива

Среднеквадратичное отклонение

Процент изделий с размером менее 19 равен 2,3%, а более 20 – 9,1%