
- •Предмет физики и методы физического исследования.
- •Механика. Кинематика. Система отсчета. Путь и перемещение.
- •Основная задача кинематики.
- •Средняя и мгновенная скорости. Ускорение и его составляющие.
- •Способы описания в прямоугольной декартовой системе отсчета движения точки.
- •Равномерное прямолинейное движение.
- •Равнопеременное прямолинейное движение.
- •Ускорение. Средняя и мгновенная скорости равнопеременного движения.
- •Прямолинейное движение с переменным ускорением.
- •Скорость равномерного прямолинейного движения. Физический смысл скорости и единицы ее измерения.
- •Ускорение равнопеременного движения. Физический смысл ускорения и единицы его измерения.
- •Средняя скорость переменного движения. Средняя скорость перемещения.
- •Скорость, путь и координата равнопеременного движения.
- •Тангенциальное ускорение движения точки по произвольной плоской кривой.
- •Нормальное ускорение движения точки по произвольной плоской кривой.
- •Кинематические характеристики вращательного движения.
- •Основные задачи динамики и пути их решения.
- •Первый закон Ньютона.
- •Второй закон Ньютона.
- •Третий закон Ньютона.
- •Импульс тела.
- •Закон Гука. Модуль Юнга (физический смысл).
- •Работа.
- •Потенциальная энергия.
- •Энергия упруго деформированного тела.
- •Термодинамический метод исследования.
- •Закон Гей-Люсака.
Нормальное ускорение движения точки по произвольной плоской кривой.
П усть
точка движется по произвольной плоской
кривой. Ее скорость при таком движении
может изменяться как по направлению,
так и по модулю (величине). За
изменение скорости только по направлению
отвечает нормальное ускорение.
Нормальное
ускорение в рассматриваемой точке
усть
точка движется по произвольной плоской
кривой. Ее скорость при таком движении
может изменяться как по направлению,
так и по модулю (величине). За
изменение скорости только по направлению
отвечает нормальное ускорение.
Нормальное
ускорение в рассматриваемой точке
,
где
R
– радиус кривизны траектории, вектор
– единичный вектор нормали к этой линии.
Нормальное ускорение направлено
перпендикулярно касательной к траектории
движения тела внутрь закругления (т.е.
вдоль радиуса кривизны). Модуль нормального
ускорения находится как
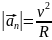 .
.
1 6.
6.
Кинематические характеристики вращательного движения.
Пусть
твердое тело, вращаясь вокруг неподвижной
оси ОО´, совершило за время dt
бесконечно малый поворот. Соответствующий
угол поворота будем характеризовать
вектором
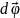 ,
модуль которого равен углу поворота, а
направление совпадает с осью ОО´ причем
так, что направление поворота отвечает
правилу правого винта по отношению к
направлению вектора
.
Модуль угла поворота в СИ измеряется в
радианах:
,
модуль которого равен углу поворота, а
направление совпадает с осью ОО´ причем
так, что направление поворота отвечает
правилу правого винта по отношению к
направлению вектора
.
Модуль угла поворота в СИ измеряется в
радианах:
 .
.
Для описания вращения тела вокруг неподвижной оси вводят следующие характеристики:
Вектор угловой скорости:
 ,
где
,
где
 – промежуток времени, за который тело
совершило поворот
.
Вектор
– промежуток времени, за который тело
совершило поворот
.
Вектор
 совпадает по направлению с вектором
.
В СИ модуль угловой скорости измеряется
в радианах в секунду:
совпадает по направлению с вектором
.
В СИ модуль угловой скорости измеряется
в радианах в секунду:
 .
.Вектор углового ускорения – характеризует изменение вектора со временем. Находится как
 .
Единицей углового ускорения в СИ
является радиан на секунду в квадрате:
.
Единицей углового ускорения в СИ
является радиан на секунду в квадрате:
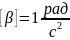 .
.Линейная скорость точки тела:
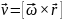 ,
где
– угловая скорость тела,
– радиус-вектор точки тела. Единицы
измерения в СИ
.
,
где
– угловая скорость тела,
– радиус-вектор точки тела. Единицы
измерения в СИ
.
Полное ускорение точки тела состоит из тангенциального ускорения (изменяет только величину линейной скорости) и нормального ускорения (изменяет только направление линейной скорости тела):
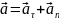 ,
где тангенциальное ускорение
,
где тангенциальное ускорение
 ,
а нормальное ускорение
,
а нормальное ускорение
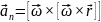 .
Модули этих ускорение:
.
Модули этих ускорение:
 ,
,
 ,
где R
– радиус кривизны траектории движения
точки. Отсюда модуль полного ускорения:
,
где R
– радиус кривизны траектории движения
точки. Отсюда модуль полного ускорения:
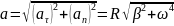 .
.
17.
Основные задачи динамики и пути их решения.
Описывая, как движется тело, как по одним характеристикам движения найти другие, кинематика не отвечает на вопрос: «Почему тело в данных условиях движется именно так, а не иначе?». Раздел механики, который выявляет причины, определяющие характер движения, и объясняет, каким образом они влияют на движение, называется динамикой.
Движение тела зависит: а) от его начального положения и начальной скорости; б) от действия на него окружающих тел (т.е. от действующих на него сил); в) от характеристик самого тела (массы тела).
В динамике решаются 2 основные задачи:
Прямая задача динамики: по заданному движению, совершаемому точкой данной массы, надо найти неизвестную действующую силу;
Обратная задача динамики: по заданным силам, действующим на точку данной массы, и заданным начальным условиям движения надо найти закон движения тела.
Основным математическим инструментом для решения задач динамики точки служат основное уравнение динамики и получаемые из него дифференциальные уравнения движения. Другими словами: пути решения задач динамики – использование законов Ньютона.
18.
