МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра вычислительной техники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

по дисциплине «Имитационное моделирование»

на тему: Моделирование систем массового обслуживания,

описываемых случайным процессом «гибели и размножения»

Факультет: АВТФ

Преподаватель: Альсова О.К. Группа: АВТ-419 Студент: Брикман Д.В.

Новосибирск

2016

Цели работы:

- изучить методы аналитического и имитационного моделирования систем в приложении к решению конкретной задачи;

- сравнить эффективность использования (простота, точность, объем вычислений) имитационных и аналитических методов для расчета показателей эффективности СМО.

Задание:

В библиотеке выдают литературу четыре библиотекаря. Время обслуживания одного читателя подчиняется экспоненциальному закону распределения с интенсивностью μ. Время прихода читателей распределено по экспоненциальному закону с интенсивностью λ. Если в очереди 2 человека, то вновь пришедший читатель покидает библиотеку. Математическое ожидание соответственно времени обслуживания: 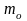= 820 секунд и времени прихода читателей = 300 секунд. При имитационном моделировании задайте количество обслуженных читателей равным 2000.

Дополнительные условия:

• очередь читателей не ограничена;

• интенсивность обслуживания читателей зависит от длины очереди: если в очереди один человек, то интенсивность обслуживания возрастает на 5%; если двое – на 10%.

Тип системы: Многоканальные системы с отказами и бесконечным потоком требований на входе (разомкнутые системы).

Исследование СМО аналитическими методами:

1. Размеченный граф состояний системы:

λ

6λ

Рис.1. Размеченный граф состояний системы

Где:

S₀ – Отсутствие заявок в системе.

S₁ – 1 заявка в системе, 1 на обработке, 0 в очереди.

S₂ – 2 заявки в системе, 2 на обработке, 0 в очереди.

S₃ - 3 заявки в системе, 3 на обработке, 0 в очереди.

S₄ - 4 заявки в системе, 4 на обработке, 0 в очереди.

S₅ - 4 заявки в системе, 4 на обработке, 1 в очереди.

S₆ - 4 заявки в системе, 4 на обработке, 2 в очереди.

Расчет многоканальных систем с отказами и бесконечным потоком требований на входе (разомкнутые системы).

= m_n^-1 = 1/300 - интенсивность входного потока

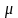= m_o^-1 = 1/820 - интенсивность обслуживания

Используемые величины:

N = 4 - число каналов обслуживания

m = 2 - количество мест в очереди

Формулы аналитического расчета характеристик СМО 2 типа:

• вероятность простоя системы:

, , ,

• вероятность нахождения в системе j-й заявки:

• вероятность загрузки системы: .

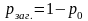• вероятность отказа в обслуживании: .

• среднее время обработки одной заявки: m₀ = 820 секунд

• среднее время пребывания требования в системе:

• среднее число требований в очереди:

.

• среднее время ожидания в очереди:

• среднее число занятых каналов:

• среднее число заявок в системе:

Вычисленные аналитические характеристики СМО:

Таблица 1. Таблица 2.

Характеристики системы: Вероятности состояний системы:

Вероятность простоя (S0)	0.063		S0	0.063
Вероятность загрузки (1 - S0)	0.937		S1	0.172
Вероятность отказа (S6)	0.0684		S2	0.235
Ср. время обработки (mo)	820		S3	0.214
Ср. число занятых каналов	2.546		S4	0.146
Ср. время ожидания в очереди	71.086		S5	0.100
Ср. число заявок в очереди	0.237		S6	0.068
Ср. время нахожд. в системе	834.985
Ср. число заявок в системе	2.783

Имитационное моделирование системы массового обслуживания:

Листинг программы имитации СМО в GPSS:

Программный расчет показателей эффективности СМО:

При расчете использовалось среднее значение по результатам 5-и прогонов программы.

Таблица 3. Таблица 4.

Характеристики системы: Вероятности состояний системы:

Вероятность простоя	0.060		S0	0.060
Вероятность загрузки	0.940		S1	0.170
Вероятность отказа	0.068		S2	0.232
Ср. время обработки	843.2		S3	0.219
Ср. число занятых каналов	2.569		S4	0.152
Ср. время ожидания в очереди	77.53		S5	0.099
Ср. число заявок в очереди	0.237		S6	0.068
Ср. время нахожд. в системе	891.4
Ср. число заявок в системе	2.807

Сопоставление результатов, полученных на основе использования аналитического и имитационного моделирования:

Как следовало ожидать, результаты имитационного и аналитического моделирования отличаются, однако различия незначительны:

Таблица 5. «Сравнение характеристик СМО»

Характеристика	Аналитические хар-ки	Имитационные хар-ки
Вероятность простоя	0.063	0.060
Вероятность загрузки	0.937	0.940
Вероятность отказа	0.068	0.068
Ср. время обработки	820	843.2
Ср. число занятых каналов	2.546	2.569
Ср. время ожидания в очереди	71.08	77.53
Ср. число заявок в очереди	0.237	0.237
Ср. время нахожд. в системе	834.9	891.4
Ср. число заявок в системе	2.783	2.807

Таблица 6.

Состояние системы	Аналитические хар-ки	Имитационные хар-ки
S0	0.063	0.060
S1	0.172	0.170
S2	0.235	0.232
S3	0.214	0.219
S4	0.146	0.152
S5	0.100	0.099
S6	0.068	0.068

Вероятности состояний системы, полученные имитационным методом, сошлись с соответствующими теоретическими значениями достаточно точно – в худшем случае расхождение составляет 0.006 (для S₄).

Остальные характеристики также достаточно близки к соответствующим теоретическим. Наибольшее расхождение наблюдается во времени ожидания в очереди. Как следствие, увеличено и среднее время нахождения в системе и среднее количество заявок в системе (длина имитируемой очереди, в среднем, больше теоретической). Также расходится среднее время обработки одной заявки.

Наблюдаемое расхождение связано, вероятно, с распределением времени генерации и обработки транзактов, отличающимся от аналитически ожидаемого (машина выдает дискретную имитацию непрерывного процесса, учитываемого в аналитических расчетах).

Оценка эффективности реализованной в работе системы массового обслуживания.

Данная СМО является достаточно эффективной, т.к. время пребывания в очереди значительно меньше времени обработки одной заявки (более чем в 10 раз). Как следствие, средняя длина очереди мала (~0.2), значит, система успешно справляется с входным потоком заявок.

Реализация имитационного моделирования СМО с учетом дополнительных условий.

Дополнительные условия:

• очередь читателей не ограничена;

• интенсивность обслуживания читателей зависит от длины очереди: если в очереди один человек, то интенсивность обслуживания возрастает на 5%; если двое – на 10%.

Листинг программы имитации СМО в GPSS:

Программный расчет показателей эффективности СМО с дополнительными условиями

Таблица 7. Таблица 8.

Характеристики системы: Вероятности состояний системы:

Вероятность простоя	0.056		S0	0.056
Вероятность загрузки	0.944		S1	0.149
Вероятность отказа	0		S2	0.304
Ср. время обработки	818.4		S3	0.208
Ср. число занятых каналов	2.689		S4	0.139
Ср. время ожидания в очереди	172.14
Ср. число заявок в очереди	0.565
Ср. время нахожд. в системе	991.2
Ср. число заявок в системе	3.25

Сравнение двух вариантов реализации системы по результатам 5-ти прогонов (I – исходный, II – с учетом дополнительных условий):

Таблица 9. «Сравнение двух реализаций системы»

Критерий	Исходная	С доп. условиями
Вероятность простоя	0.060	0.056
Ср. время обработки	843.2	818.4
Ср. время ожидания в очереди	77.53	172.14
Ср. число заявок в очереди	0.237	0.565
Макс. содержимое очереди	2	13
Ср. время нахожд. в системе	891.4	991.2

Как видно из таблицы, система с дополнительными условиями справляется с нагрузкой немного хуже, чем исходная система (увеличилась средняя длина очереди, время ожидания в очереди и время пребывания в системе). Это связано с возросшей нагрузкой на систему вследствие снятия ограничения длины очереди. Несмотря на дополнительное условие в виде увеличения интенсивности обслуживания, максимальное содержимое очереди достигало 13-и заявок. Как следствие, возросло среднее время ожидания в очереди и время пребывания в системе в целом, а вероятность загрузки системы при этом увеличилась незначительно.