6. 3. Метод коэффициентов ошибки

Идея метода очень проста: разложить передаточную функцию K_ξx(р) в ряд по степеням комплексной переменной р, а затем, записав в операторной форме дифференциальное уравнение системы, обратным преобразованием Лапласа обеих его частей перейти к традиционной форме записи через производные.

Рассмотрим эту идею более подробно. Передаточная функция может быть записана по формуле (6.9), но для удобства разложения в ряд ее необходимо представить в виде дробно-рациональной функции параметра р, т. е. в виде отношения двух полиномов. Интересной особенностью функции К_ξх(р) является тот факт, что она представляет со­бой отношение двух характеристических полиномов: разомкнутой системы А(р) и замкнутой системы G(р). В самом деле, если обозна­чим передаточную функцию разомкнутой системы в виде

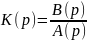
то знаменатель этой передаточной функции будет называться характеристическим полиномом разомкнутой системы.

С другой стороны, передаточная функция замкнутой системы тоже имеет свой знаменатель:

Полином G (р) называется характеристическим полиномом замкнутой системы. Обратим внимание: это сумма числителя и знаменателя передаточной функции разомкнутой системы К(р). Теперь, переходя к формуле (6.9), можно записать:

что и является отношением двух характеристических полиномов.

Отношение этих полиномов можно представить в виде некоего третьего полинома, так называемого полинома ошибки с пока что неизвестными коэффициентами:

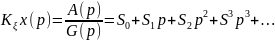(6.12)

В принципе, этот полином бесконечен, так как в общем случае невозможно ожидать, чтобы два различных полинома разделились без остат­ка.

Коэффициенты полинома S₀, S₁, S₂, … называются коэффициентами

ошибки.

Формулу (6.12) можно записать в более удобном виде. Так как передаточная функция есть отношение изображений двух сигналов, то

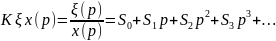
Записав это в одну строку, получим

ξ (р) = x(р)(S_{0 +} S₁p + S₂p² + S₃p³ + ...),

или, переходя от операторной (символической) формы записи дифференциального уравнения к классической, получаем:

(6.13)

Таким образом, если определить неизвестные пока коэффициенты ошибки S₀, S₁, S₂, S₃, ..., то искомая ошибка регулирования за­писывается в аналитической форме через входной сигнал х(t) и его производные. Это настолько удобно, что не следует жалеть усилий для определения коэффициентов ошибок.

Самый удобный способ определения коэффициентов ошибки – выразить их через известные коэффициенты характеристических полиномов А (р) и G (р).

Запишем эти полиномы в виде:

A(p)=C_npⁿ + C_n-1p^n-1 + ... C₁p + C₀;

G(p)=A_npⁿ + A_n-1p^n-1 + A₁p + A₀ (6.14)

Эти записи показывают, что порядок характеристических полино­мов замкнутой и разомкнутой систем одинаков. Это не случайно. Если вернуться к формуле (6.11), то видно, что в G (p) = A(p) + B(p). Ясно, что порядок полинома G (р) будет определяться порядком того полинома A(р) или В (р), который содержит переменную р в более высокой степени. Как известно, В(р) - числитель передаточной функции К (р), а А(р) h ее знаменатель.

Для всех практически встречающихся автоматических систем порядок полинома A(р) выше, чем полинома В(р), так как наиболее часто встречающиеся структурные звенья: инерционные, интегрирующие, колебательные - имеют порядок р в знаменателе своих передаточных функций выше, чем в числителе. Поэтому можно считать, что порядок полинома G (р) определяется порядком полинома A(р). Возвращаясь к формуле (6.12) и подставляя туда (6.14), путем деления двух поли­номов легко найти коэффициенты третьего. В частности,

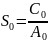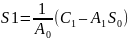; ; (6.15)

;

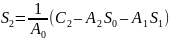и т. д.

Здесь: А₁, А₂, А₃, ... - коэффициенты полинома G(р); С₀, С₁, C₂ ... - коэффициенты полинома А(р).

Полученные формулы для коэффициентов ошибки интересны не только тем, что позволяют их рассчитать, но и тем, что открывают ясный путь к пониманию сущности астатизма. Они позволяют понять, почему наличие именно интегрирующих звеньев превращает систему в астатическую и уменьшает ошибку регулирования.

Рассмотрим несколько примеров.

Пример 6. 3. Возьмем статическую систему

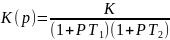
Для такой системы

C₀ = 1; С₁ = T₁ + T₂; С₂ = T₁T₂;

A₀ = 1 + K; A₁ = T₁ + T₂; A₂ = T₁T₂

Ни один коэффициент не равен нулю или бесконечности. Следовательно, как видно из (6.15), все коэффициенты ошибки отличны от нуля.

Тогда в формуле (6.13) присутствуют все слагаемые и даже при постоянном воздействии на входе системы x(t) = A ошибка ξ (1) бу­дет конечной, не равной нулю:

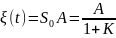
Пример 6. 4. Превратим систему в астатическую 1-го порядка:

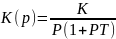
A (p) = P + P²T; С₀ = 0; С₁ = 1; С₂ = T;

G (p) = K + P + P²T; A₀ = K; A₁ = 1; A₂ = T

Наличие интегрирующего звена приводит к отсутствию в знаменателе свободного члена не содержащего р. Отсюда - равенство нулю коэффициента С₀ и, как следствие, коэффициента S₀. Остальные коэффициенты С₁, C₂ не равны нулю, поэтому и S₁, S₂, ... тоже не равны нулю. Теперь, при подаче на вход системы постоянного воздействия, ошибки не будет:

ξ (t)=S₀A=0A=0

При подаче на вход линейно возрастающей функции х(t)=Аt ошибка будет, но она будет постоянной:

Пример 6. 5. Увеличим астатизм системы, добавив еще одно интегрирующее звено:

T₁>T₂

(для устойчивости системы)

A (p) = P² + P³T₂; C₀ = C₁ = 0; C₂ = 1; С₃ = T₂;

G(p) = K + KpT₁ + P² + P³T₂; A₀ = K; A₁ = KT₁; A₂ = 1; A₃ = T₃.

Если воспользоваться формулами (6.15), то легко видеть, что два первых коэффициента ошибки равны нулю и в формуле (6.13) уже будут отсутствовать первые два слагаемых. Теперь при подаче на вход сигнала x(t) = At ошибка будет равна нулю.

Таким образом, наблюдается очень интересная закономерность: с возрастанием порядка астатизма исчезают, начиная с S₀, коэффициенты ошибки, а в формуле (6.13) исчезают слагаемые, начиная с пер­вого. Однако не следует увлекаться астатизмом высоких порядков: интегрирующие звенья вносят фазовый сдвиг по -90 каждое. Поэтому уже при втором порядке астатизма возникают проблемы с устойчи­востью системы. В связи с этим появляется необходимость вводить в систему дополнительные, так называемые корректирующие звенья. Тем не менее системы с порядком астатизма выше второго практически не используются. Однако не следует отчаиваться: уничтожение в формуле (6.13) даже первых двух слагаемых очень сильно уменьшает ошибку регулирования, так как эти слагаемые самые мощные и именно они вносят основной вклад в формирование ошибки регулирования.