4.1.4. Графическое оформление полученных результатов
Графическое представление данных делает наглядным изображение полученного распределения результатов исследования. Это обстоятельство дает возможность с одного взгляда определить структуру и состав изучаемой совокупности, структурные сдвиги, тенденции изменений и т.д.
Указанные выше компьютерные программы предлагают достаточно большой набор графического оформления: гистограммы, графики, диаграммы круговые, точечные, кольцевые, пузырьковые и т.д. В конечном счете выбор того или иного варианта – дело вкуса и чувства меры.
Наиболее часто используются такие виды графического представления данных, как гистограмма, различные виды диаграмм, полигон распределения.
Гистограмма – графическое изображение интервального ряда.
Пример 4.4. Распределение ответов на вопрос о способах
проведения досуга
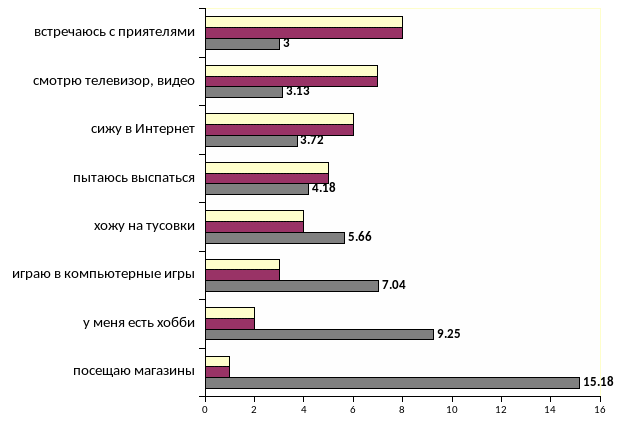
Круговая диаграмма – график распределения частот для номинальной переменной. Представляет круг, разделенный на секторы, соответствующие значениям переменной. Секторы раскрашиваются в различные цвета; соответствие между цветами и значениями переменной устанавливается с помощью легенды.
Пример 4.5. Распределение абитуриентов по полу.
Полигон распределения – график распределения частот для порядковых и количественных переменных. Представляет собой
ломаную линию, наглядно демонстрирующую распределение частот.
Пример 4.3. Полигон распределения
Для дискретной переменной данное распределение строится в пространстве двух координатных осей: по оси абсцисс традиционно представляются значения переменной, упорядоченные по возрастанию, по оси ординат – их частоты.
4.2. Статистический анализ данных
Формат данного учебного пособия не предполагает описание математико-статистического аппарата, поэтому ниже будут рассмотрены только возможности использования инструментов статистики для анализа эмпирических данных.
4.2.1. Измерение центральной тенденции
Для того чтобы в полученной числовой информации можно было выявить типичные характеристики, рассчитывают средние величины или меру центральной тенденции.
Средние величины – это обобщающие показатели, в основе которых могут лежать как количественные, так и качественные признаки. В первом случае, это может быть средний возраст сотрудников, средняя оценка на курсе по какой-то дисциплине и т.д. Во втором – типичный для большинства группы респондентов мотив получения образования, уровень удовлетворенности учебой и так далее. Отсюда назначение меры центральной тенденции − служить сводными количественными характеристиками, обеспечивающими наилучшее описание множества наблюдений или оценок.
Важным условий применения средних величин является их расчет на качественно однородной совокупности. Это требование предполагает, например, что намереваясь выявить отношение к учебе типичного студента, мы не будем усреднять оценки отличников и тех, кто еле-еле переползает с курса на курс.
Простая среднеарифметическая величина применяется в том случае, если в исходных данных значение каждого варианта встречается один раз. Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5.
Средняя арифметическая взвешенная используется, если имеется некоторая повторяемость значений единиц совокупности, поскольку позволяет учесть различную численность вариантов. Употребление простой среднеарифметической в этих случаях недопустимо, так как это неизбежно приводит к искажению. Например, на предприятии 10 работников со стажем работы до 3 лет, 20 - со стажем от 3 до 5 лет, 5 работников - со стажем более 5 лет. В этом случае средний стаж работников нужно рассчитывать по формуле средней арифметической взвешенной, приняв в качестве середины интервалов стажа каждого варианта 2, 4 и 6 лет соответственно. Для характеристики структуры совокупности применяются особые показатели, которые называются структурными средними. К таким показателям относятся мода и медиана.
Мода представляет собой наиболее часто встречающееся или типичное значение. Мода – именно то число, которое в действительности встречается чаще всего (является величиной определенной). Например, наиболее часто встречающееся значение в 10-балльной шкале оценки степени удовлетворенности отношениями в группе.
Медиана – это число в середине набора чисел: половина чисел имеют значения большие, чем медиана, а половина чисел — меньшие. В примере с оценкой медианным значением будет число 5.
При симметричном распределении набора чисел все три значения центральной тенденции будут совпадать. При несимметричном распределении набора чисел они могут быть разными.