Физическое моделирование

Физическое моделирование – это исследование поведения объекта в тех или иных условиях путем экспериментального изучения его физической модели.

Физическое моделирование сводится к воспроизведению постоянства определяющих критериев подобия в модели и объекте.

Физическое моделирование основано на использовании теории подобия. Подобными называются объекты, у которых все характеризующие их величины в любой точке пространства находятся в одинаковых взаимных отношениях.

Поскольку любой процесс протекает в определенном геометрическом пространстве, то, прежде всего, устанавливают геометрическое подобие и лишь затем физическое подобие, характеризующее протекающий процесс.

1. Геометрическое подобие.

Отношение одноименных размеров модели и натурального объекта называется масштабом модели. Взяв какой-либо линейный размер модели l_м и разделив его на соответствующий размер объекта l_о, получим линейный масштаб модели:

.

Например, для двух аппаратов,

у которых диаметры равны D_о и D_м, высота слоя перемешиваемой жидкости H_о и H_м, диаметры лопастей мешалок d_о и d_м, а высоты лопастей h_о и h_м, в условиях геометрического подобия будет соблюдаться равенство:

,

где

Однако, геометрическое подобие аппаратов удобнее выражать, вводя определяющий геометрический размер. Так, если в рассматриваемой модели аппарата за определяющий размер принять диаметр лопасти мешалки d_м и сравнить с ним все остальные размеры:

,

то геометрическое подобие будет соблюдаться, если в любом другом аппарате при той же определяющей характеристике сохранятся одинаковые значения безразмерных отношений i_D, i_H, i_h, т.е.

Безразмерные отношения и т.д., сохраняющие одно и тоже значение в модели и объекте, называются инвариантами геометрического подобия.

Таким образом, геометрическое подобие будет соблюдаться, если инварианты геометрического подобия в сравниваемых системах сохраняют одно и тоже значение, т.е.

, , .

2. Физическое подобие.

По аналогии с геометрическим подобием, физическое подобие соблюдается, когда в сравниваемых системах его инварианты сохраняют одно и тоже значение. При этом инварианты физического подобия так же должны быть безразмерными величинами. Одним из способов составления безразмерных отношений является преобразование дифференциальных уравнений к безразмерному виду.

В качестве примера рассмотрим преобразование уравнения движения вязкой жидкости Навье-Стокса. Рассмотрим движение элементарного объема жидкости со сторонами dx, dy, dz вдоль оси dz. Тогда уравнение одномерного установившегося движения потока относительно оси z будет иметь вид:

,

где  = ·g – сила тяжести;

ρ и μ – плотность и вязкость жидкости, соответственно;

Р_z, w_z – составляющие давления и скорости вдоль оси z;

τ – время.

Умножим все члены этого уравнения на dz, что равносильно изменению всех параметров по длине dz:

Это уравнение представляет собой математическую модель движущейся вязкой жидкости, обладающей инерцией и перемещающейся под действием силы тяжести , давления и трения .

В уравнении силы отнесены к элементу объема и действуют на отрезке длинной dz.

Заменим дифференциальные выражения действующих сил конечными:

- для силы инерции:

,

- для силы тяжести:

,

- для силы давления:

,

- для силы трения:

,

и проведем сопоставление всех действующих сил с силой инерции.

Взяв отношение силы инерции к силе тяжести и помня, что =g, получим:

Полученный комплекс называют числом Фруда, который является инвариантом физического подобия по действию сил тяжести.

Взяв отношение сил давления к силе инерции, получим:

Полученный комплекс называют числом Эйлера, который является инвариантом физического подобия по действию сил давления.

Взяв отношение силы инерции к силе трения, получим:

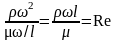
Полученный комплекс называют числом Рейнольдса, который является инвариантом физического подобия по действию сил внутреннего трения или сил молекулярной вязкости.

Представление уравнений в безразмерном виде позволяет использовать их для широкого класса физических явлений. Эти уравнения позволяют осуществлять масштабный перенос рассматриваемых явлений и реализовать, таким образом, физическое моделирование.

Однако не для всякого объекта может быть создана физическая модель. В тех случаях, когда число рассматриваемых явлений велико и соответственно велико число определяющих критериев подобия, практически не возможно обеспечить их одновременное равенство в модели и объекте и достичь тем самым необходимого физического подобия. По этой причине возможности физического моделирования, основанного на теории подобия, существенно ограничены сложностью изучаемого объекта. В химической технологии физическое моделирование широко применяется при изучении сравнительно простых систем (гидравлических, тепловых, диффузионных), т.е. при анализе детерминированных процессов, описываемых законами классической механики и протекающих в однофазных системах с фиксированными границами.

Для анализа стохастических процессов, таких как двухфазные системы со свободными поверхностями и процессов, осложненных химическими реакциями, использование физического моделирования затруднено.

Применение этого метода осложняется также непреодолимыми трудностями непосредственного исследования слишком медленно или слишком быстро протекающих процессов и явлений (образование каменного угля, молекулярные колебания) или опасностью экспериментов (ядерные реакции). Следует отметить так же низкую эффективность мелкомасштабного физического моделирования при изучении больших и сложных производственных и экологических систем.

Достоинства метода физического моделирования:

• наглядность, т. к. физическая модель воспроизводит практически все стороны исследуемого оригинала.

• возможно изучение процесса без составления его математического описания

• возможность воспроизведения производственного процесса в лaборaторных условиях.

Недостатки метода физического моделирования:

• отсутствие универсальности, т.к. для каждого нового процесса необходимо создавать новую модель

• высокая стоимость моделей для исследования сложных процессов

• невозможность применения этого метода для моделирования большей части химических процессов и реакторов, а также других сложных объектов.

Любой химико-технологический процесс, как правило, сопровождается перемещением некоторых материальных потоков жидкости, газа или твердых частиц. Структура потоков оказывает существенное влияние на эффективность химико-технологических процессов. При этом математическая модель структуры потока является основой для построения математической модели процесса в целом.