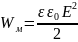- •1. Электрическое поле. З-н Кулона
- •2. Напряженность электрического поля. Принцип суперпозиции электр. Полей.
- •3. Работа по перемещения заряда в электрическом поле. Потенциал. Разность потенциалов
- •4.Работа электростатич. Заряда по перемещению единичного положительного заряда из одной точки поля в другую.
- •5. Связь напряженности с потенциалом. Циркуляция вектора напряженности электростатического поля.
- •6. Поток вектора напряженности. Теорема Остроградского – Гауса
- •7.Применение теор. Остр-Гауса для расчета электростат. Поля
- •8.Проводники в электростатическом поле
- •9.Электрическая ёмкость проводника. Ёмкость конденсатора
- •- Электроемкость плоского конденсата
- •10.Энергия заряженного проводника. Энергия заряженного конденсатора. Объёмная плотность энергии электрического поля
- •- Элементарная работа
- •11.Диэлектрики в электрическом поле
- •12.Электрический ток и его хар-ки
- •13.Закон Ома. Сопротивление цепи
- •14 Работа и мощность тока. Закон Джоуля-Ленца.
- •15 Стороние силы. Эдс и напряжение. Закон Ома для неоднородного участвка цепи
- •16 Правила Кирхгофа
- •17. Магнитное поле и его характеристики. Сила Ампера
- •18. Движение заряженных частиц магнитным полем. Сила Лоренца
- •19. Закон Био-Савара-Лапласа
- •20. Магнитное поле движущегося заряда
- •21. Применение закона био-савара-лапласа для расчета магнитных полей
- •22. Электрический ток в вакууме. Термоэлектронная эмиссия. Законы описывающие электрический ток в вакууме
- •23. Эл. Ток в газах. Самостоятельные и несамостоятельные заряды. Понятие о плазме
- •24 Циркуляция вектора магнитного поля. Закон полного тока
- •25. Теорема Гауса для магнитного поля
- •26. Работа по перемещению проводника и витка с током в магнитном поле
- •27. Вращательный момент действующий на виток с током в магнитном поле. Потенциальная энергия витка
- •28. Явление электромагнитной индукции. Правило Ленца
- •29.Явление самоиндукции. Индуктивность.
- •30. Ток при замыкании и размыкании цепей
- •31.Энергия магнитного поля. Плотность энергии.
- •32 Гармонические колебания и их характеристики. Дифференц. Уравнение гармонических колебаний
- •33.Механические гармонические колебания
- •34.Свободные колебания в колебательном контуре
- •35 Сложение колебаний.
- •36.Свободные затухающие колебания. Дифференциальное уравнение затухающих колебаний
- •37.Вынужденные колебания. Резонанс
- •38.Плоские синусоидальные волны. Фазовая скорость. Длина волны. Волновое число
- •39. Интерференция волн
- •40.Стоячие волны.
29.Явление самоиндукции. Индуктивность.
Электрический ток текущий в замкнутом контуре создаёт вокруг себя магнитное поле индукция которого пропорциональна силе тока Б-С-Л. Сцепление с контуром магнитного потока(потокосцепление)
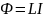 ,
L-индуктивность
контура
,
L-индуктивность
контура
При изменении силы тока в контуре так же будет изменятся сцепление с ним магнитного потока

Следовательно в контуре будет возникать ЭДС индукции .ЭДС индукции в контуре при изменении силы тока в нём
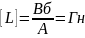
Для длинного соленоида
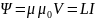 ,
,
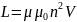 ,
,
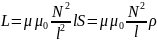 ,
,
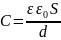 ,
,
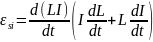
Если
 ,
,
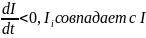
Контур обладающий определённой индуктивностью приобретает электрическую энергию, заключ. в том, что любое изменение тока тормозится и тем больше, чем индуктивность L.
30. Ток при замыкании и размыкании цепей
П о
правилу Ленца, дополнительные токи,
возникающие вследствие самоиндукции
, всегда направлены так, чтобы
противодействовать изменению тока в
цепи.
о
правилу Ленца, дополнительные токи,
возникающие вследствие самоиндукции
, всегда направлены так, чтобы
противодействовать изменению тока в
цепи.
Э то
приводит к тому, что установление тока
при замыкании цепи и убывание тока при
размыкании цепи происходит не мгновенно,
а постепенно.
то
приводит к тому, что установление тока
при замыкании цепи и убывание тока при
размыкании цепи происходит не мгновенно,
а постепенно.
Найдем
сначала характер изменения тока при
размыкании цепи. Пусть в цепь,
индуктивностью L
и сопротивлением R
включить источник тока и переключить
и переключатель находится в положении
2. Тогда в цепи будет течь ток
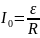 .
.
В
момент времени t=0
отключают источник тока(переключают
в положение 1). Как только сила тока
начнет убывать, возникающая εi
, противодействующая этому убыванию
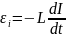 .По
второму правилу Кирхгофа:
.По
второму правилу Кирхгофа:
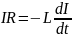 .
.
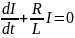 –
мы получили однородное ДУ-1. Разделяя
переменные получим:
–
мы получили однородное ДУ-1. Разделяя
переменные получим:
 ,
,
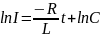 ,
c
– const
можно найти из начальных условий. При
t=0
→
,
c
– const
можно найти из начальных условий. При
t=0
→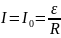 .
.
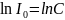 ,
→
,
→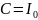 .
.
Частное
решение:
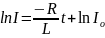 ,
,
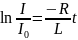 ,
,
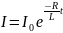
Рассмотрим
случай замыкания цепи из 1 в 2. После
подключения источника тока до тех пор,
пока сила тока не достигнет установленного
значения:
в цепи кроме ε возникает также
,
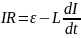 ,
,
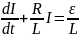 .
Мы получили неоднородное ДУ-1. Решением
неоднородного уравнения является сумма
общего решения соответствующего
однородного уравнения и частного
решения соответствующего неоднородного
уравнения:
.
Мы получили неоднородное ДУ-1. Решением
неоднородного уравнения является сумма
общего решения соответствующего
однородного уравнения и частного
решения соответствующего неоднородного
уравнения:
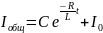 .
Легко видеть, что частным решением
является
,
константу находим из начальных условий
при t=0,
I=0.
.
Легко видеть, что частным решением
является
,
константу находим из начальных условий
при t=0,
I=0.
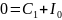 ,
,
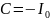 ,
,
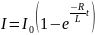 .
.
31.Энергия магнитного поля. Плотность энергии.
Проводник по которому протекает электрический ток всегда определяет магнитное поле
Причём магнитное поле появляется и исчезает вместе с появлением и исчезновением электрического тока. Следовательно часть энергии тока идёт на создание магнитного поля, который подобно электричеству является носителем энергии. Энергия магнитного поля равна работе ,который затрачивается током не создающим магнитного поля
Рассмотрим контур с током индуктивность которого L,с данным контуром сцепляется магнитный поток
Причём при изменении тока на dI приводит к изменению магнитного потока
Для изменения магнитного потока на величину dФ необходимо совершить работу
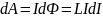
Тогда работа будет равна
 ;
;
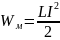
Выразим энергию магнитного поля через характеристику магнитного поля
;
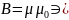 ;
;
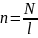 ;
;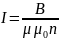 ;
;
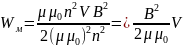
Энергия сосредоточенная в единице объёма (объёмная плотность энергии магнитного поля)
 ;
;