Операции над событиями

Определение 1. Говорят, что в некотором опыте событие А влечёт за собой появление события В, если при наступлении события А наступает и событие В. Обозначение этого определения А Ì В. В терминах элементарных событий это означает, что каждое элементарное событие, входящее в А, входит также и в В.

Определение 2. События А и В называются равными или эквивалентными (обозначается А = В), если А Ì В и В Ì А, т.е. А и В состоят из одних и тех же элементарных событий.

Достоверное событие представляется объемлющим множеством Ω, а невозможное событие – пустым подмножеством Æ в нём. Несовместность событий А и В означает, что соответствующие подмножества А и В не пересекаются: А∩В = Æ.

Определение 3. Суммой двух событий А и В (обозначается С = А + В) называется событие С, состоящее в наступлении по крайней мере одного из событий А или В (союз «или» для суммы является ключевым словом), т.е. наступает или А, или В, или А и В вместе.

Пример. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B — в том, что в мишень попадает 2-й стрелок. Событие A + B означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков (1-й стрелок или 2-й стрелок, или оба стрелка).

Аналогично, суммой конечного числа событий А₁, А₂, …, А_n (обозначается А = А₁ + А₂ + … + А_n) называется событие А, состоящее в наступлении хотя бы одного из событий А_i (i = 1, … , n), или произвольной совокупности А_i (i = 1, 2, … , n).

Пример. Суммой событий А, В, С является событие, состоящее в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С, А или В, А или С, В или С, А или В или С.

Определение 4. Произведением двух событий А и В называется событие С (обозначается С = А ∙ В), состоящее в том, что в результате испытания произошли и событие А, и событие В одновременно. (Союз «и» для произведения событий является ключевым словом).

Аналогично произведением конечного числа событий А₁, А₂, …, А_n(обозначается А = А₁ ∙А₂ ∙…∙ А_n) называется событие А, состоящее в том, что в результате испытания произошли все указанные события.

Пример. Если события А, В, С есть появление «герба» в первом, во втором и третьем испытании соответственно, то событие А × В × С есть выпадение «герба» во всех трех испытаниях.

Замечание 1. Для несовместных событий А и В справедливо равенство А ∙ В = Æ, где Æ – невозможное событие.

Замечание 2. События А₁, А_{2, … ,} А_n образуют полную группу попарно несовместных событий, если  .

Определение 5. Противоположными событиями называются два единственно возможных несовместных события, образующие полную группу. Событие, противоположное событию А, обозначается  . Событие   противоположное событию А, является дополнением к событию А до множества Ω.

Для противоположных событий одновременно удовлетворяются два условия А ∙  = Æ и А +  = Ω.

Определение 6. Разностью событий А и В (обозначается А – В) называется событие, состоящее в том, что событие А наступит, а событие В – нет и она равна А – В = А× .

Отметим, что события А + В, А ∙ В,  , А – В удобно трактовать в графическом виде с помощью диаграмм Эйлера – Венна 

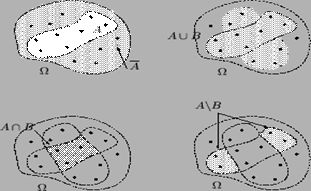
Операции над событиями: отрицание, сумма, произведение и разность

Сформулируем пример так: пусть опыт G заключается в проведении стрельбы наугад по области Ω, точки которого являются элементарными событиями ω. Пусть попадание в область Ω есть достоверное событие Ω, а попадание в области А и В – соответственно события А и В. Тогда события  , А+В (или А È В – светлая область на рисунке), А ∙ В (или А Ç В – область в центре), А – В (или А \ В – светлые подобласти) будут соответствовать четырем изображениям на рисунке. В условиях предыдущего примера со стрельбой двух стрелков по мишени произведением событий А и В будет событие С = А Ç В, состоящее в попадании в мишень обоими стрелками.

Замечание 3. Если операции над событиями представить как операции над множествами, а события представить как подмножества некоторого множества Ω, то сумме событий А+В соответствует объединение АÈВ этих подмножеств, а произведению событий А ∙ В — пересечение А∩В этих подмножеств.

Таким образом, операции над событиями можно поставить в соответствие операцию над множествами. 

Обозначения	Язык теории вероятностей	Язык теории множеств
Ω	Пространство элемент. событий	Универсальное множество
	Элементарное событие	Элемент из универсального множества
А	Случайное событие	Подмножество элементов ω из Ω
Ω	Достоверное событие	Множество всех ω
Æ	Невозможное событие	Пустое множество
АÌ В	А влечёт В	А – подмножество В
А+В (А ÈВ)	Сумма событий А и В	Объединение множеств А и В
А× В (А Ç В)	Произведение событий А и В	Пересечение множеств А и В
А – В (А \ В)	Разность событий	Разность множеств
	– событие, противоположное событию А, т.е. не А	Дополнение множества А до множества Ω  = Ω \ А

Действия над событиями обладают следующими свойствами:

• А + В = В + А, А ∙ В = В ∙ А (переместительное);

• (А + В) ∙ С = А × С + В × С, А ∙ В + С = (А + С) × (В + С) (распределительное);

• ( А + В ) + С = А + (В + С), (А ∙ В) ∙ С = А ∙ (В ∙ С) (сочетательное);

• А + А = А, А ∙ А = А;

• А + Ω = Ω, А ∙ Ω = А;

• А +   = Ω, А ∙  = Æ;

•   = Ω,   = Æ,   = А;

• А – В = А ∙  ;

•   и   — законы де Моргана.

В справедливости этих свойств можно убедиться с помощью диаграмм Эйлера-Венна, а также на основе численного подхода, если сопоставить появлению некоторого события цифру «1», а не появлению этого события – цифру «0». Тогда следующие операции над событиями: А + В, А ∙ В,   – иллюстрируются в следующей таблице.

А	В	А+В	А ∙ В	А
1	1	1	1	1	0
1	0	1	0	0	1
0	1	1	0
0	0	0	0

Законы де Моргана доказываются путем составления табл.

А	В			А+В				А∙В
1	1	0	0	1	0	0	0	1	0
1	0	0	1	0	0	0	1	0	1
0	1	1	0	1	0	0	1	0	1
0	0	1	1	0	1	1	1	0	1