Тест «ковариация»

Ковариационной функцией случайной последовательности называется функция целочисленной переменной :

Если -- независимые, одинаково распределённые по закону R(0,1) случайные величины, то и независимы для любого и следовательно :

(7)

Пусть -- оценка по выборке , полученной в результате - кратного обращения к исследуемому датчику :

где 1<t<< -- выборочное среднее. Заметим , что - выборочная дисперсия).

Тест «ковариация» позволяет проверить свойство (7) (гипотезу ) для последовательности и описывается следующим решающим правилом :

принимается (8)

где : для Δ - порог, определённый для заданного уровня значимости по формуле :

Δ = Ф^-1(1 - ).

В пакете СТАТМОД предполагается использование эквивалентной формы правила (8) :

принимается

где

Представим (8) в виде:

принимается (9)

Здесь - верхняя и нижняя доверительные границы для , соответствующие доверительной вероятности

Решающее правило в форме (9) удобно использовать при визуальном анализе графиков ковариационной функции и её оценки .

Тест «равномерность двухмерного распределения»

Из выборочных значений полученных в результате - кратного обращения к датчику БСВ построим ([ ]-целая часть числа ) векторов :

(10)

Единичный квадрат с центром в точке разобьём на ячеек :

где -- произвольные вещественные числа.

Вычислим частоты попадания точек с координатами (10) в ячеек гиперкуба.

Если -- независимые, одинаково распределённые по закону R(0,1) случайные величины, то теоретические вероятности попадания точек с координатами в ячейки равны площадям этих ячеек :

Описываемый тест используется для проверки гипотезы Н₀ о равномерности двухмерного распределения векторов и представляет собой следующее решающее правило:

принимается (11)

где в случае истинной гипотезы H₀ и статистика

(12)

имеет x² – распределение с k – 1 степенями свободы, а порог Δ определяется как квантиль этого распределения: , где ε – заданный уровень значимости.

В пакете СТАТМОД предполагается использование эквивалентной формы правила (11):

принимается

где Р - значение вычисляется по формуле: P=1-F(x²), здесь F(.)- функция распределения статистики (12).

1.1.2.Статический анализ точности моделирования

Тесты проверки точности моделирования БСВ допускают графическую интерпретацию, удобную для быстрого визуального анализа качества смоделированной выборки реализаций БСВ.

В пакете СТАТМОД реализованы следующие графики:

1. диаграмма рассеяния (иллюстрирует зависимость между a_i и a_t-1 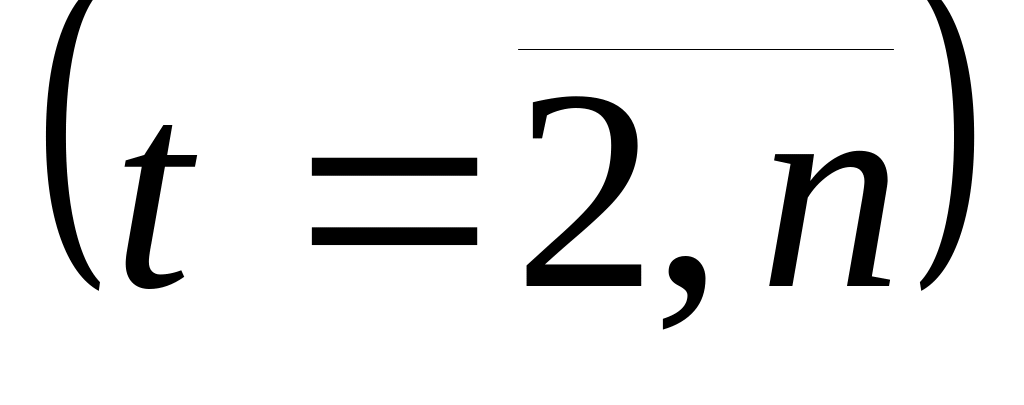; для проверки факта наличия зависимости используется тест «ковариация»);

2. гистограмма и плотность распределения (позволяет осуществить сравнительный анализ теоретического и эмпирического распределения выборки А; для проверки согласия распределения А с равномерным законом используются критерии согласия);

3. график корреляционной функции с указанием доверительных границ (служит для графической поддержки теста «ковариация»);

4. визуализация выборки (иллюстрирует зависимость a_i от t 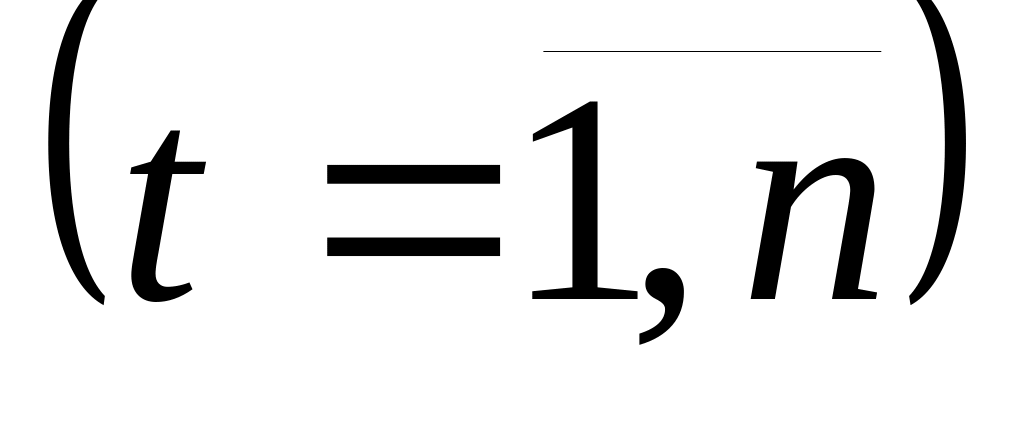и может использоваться для графической поддержки критериев серий).