Глава 1.Принципы моделирования случайных элементов

При компьютерном моделировании случайных процессов и систем возникает необходимость в моделировании различных случайных элементов : случайных величин, случайных векторов, процессов, полей, множеств.

Моделирование на ЭВМ случайного элемента подчиняется следующим двум основным принципам.

1. Сходство между случайным элементом-оригиналом и его моделью 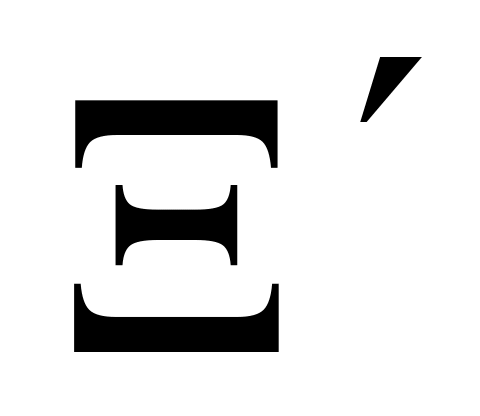состоит в совпадении (близости) вероятностных законов распределения или их числовых характеристик;

2. Всякий случайный элемент определяется («конструируется») как некоторая функция от простейших случайных элементов, называемых базовыми случайными величинами (БСВ) (см. раздел «Моделирование БСВ»):

(1)

Таким образом, задача моделирования произвольного случайного элемента разбивается на следующие подзадачи.

1. Моделирование на ЭВМ независимых БСВ ;

2. Осуществление функционального преобразования (1) с помощью соответствующей функции .

Для моделирования одного и того же случайного элемента может быть предложено несколько вариантов функциональных преобразований (1). Предпочтение отдаётся варианту , использующему меньшее число БСВ для моделирования одной реализации случайного элемента , то есть требующему меньших вычислительных затрат. Такому варианту соответствует максимальное значение коэффициента использования БСВ :

.

В качестве объектов моделирования в пакете СТАТМОД используются следующие

случайные элементы :

• случайные (скалярные) величины;

• случайные векторы;

• случайные процессы.

Графический анализ результатов моделирования включает следующие графики :

• визуализация выборки (иллюстрирует зависимость от 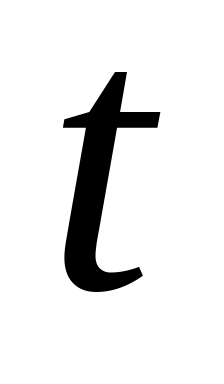и может использоваться для графической поддержки критериев серий);

• графики эмпирической и теоретической функций распределения (графики функций и );

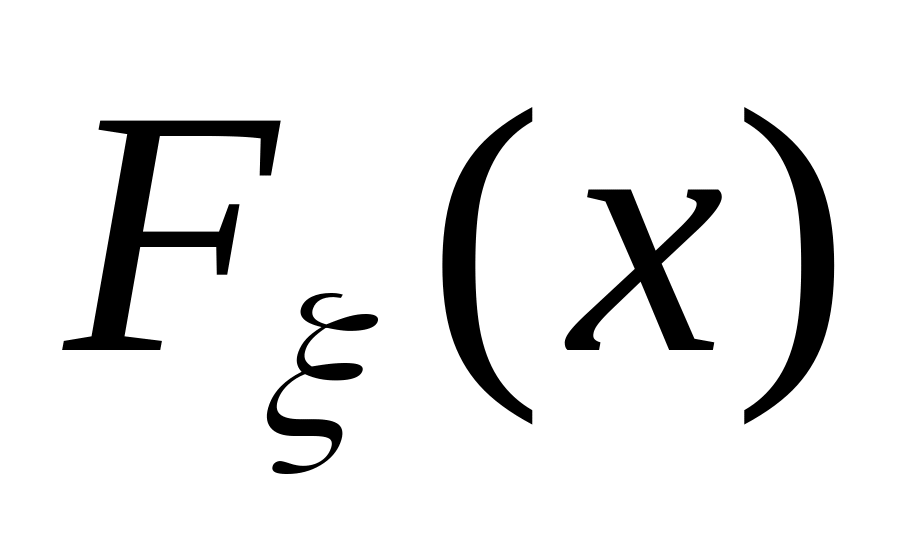• графики эмпирической и теоретической функций вероятности (графики функци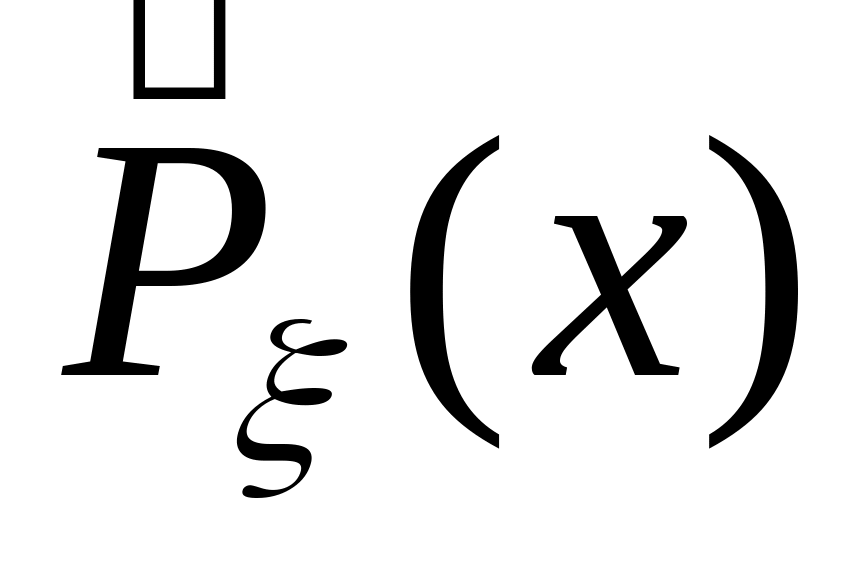й и )).

Два последних графика позволяют осуществлять сравнительный анализ теоретического и эмпирического распределений выборки и могут служить в качестве графической поддержки критериев согласия.

1.1. Моделирование случайных величин

1.1.1.Моделирование базовых случайных величин (бсв) Понятие бсв

Базовой случайной величиной (БСВ) непрерывная СВ , равномерно распределённая на полуинтервале [0,1).

Равномерный на [0,1) закон обозначается R(0,1).

БСВ имеет следующие функциональные и числовые характеристики :

• функция распределения :

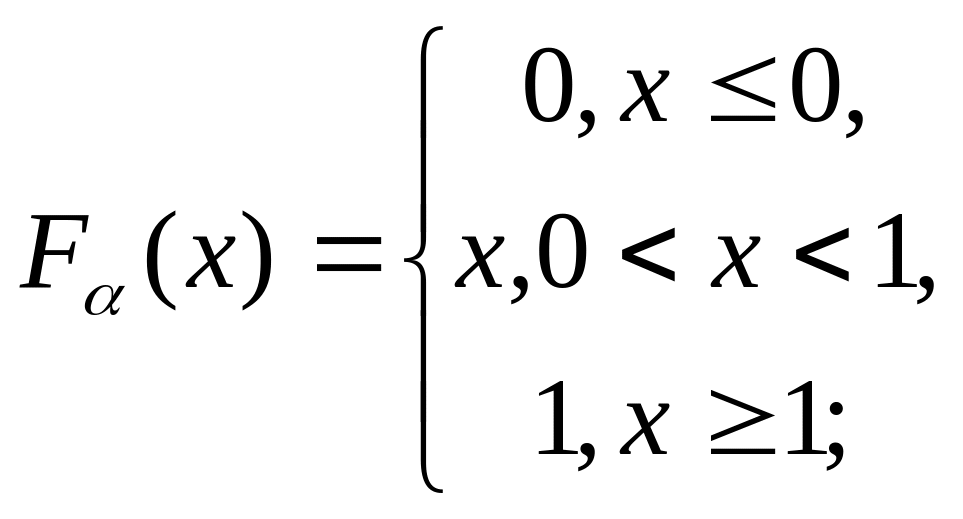
• плотность распределения :

• математическое ожидание (среднее значение) :

• дисперсия :

Датчики бсв

Для моделирования на ЭВМ реализаций БСВ используются специальные программы, называемые программными датчиками БСВ.

В основе программных датчиков БСВ лежат рекуррентные формулы вида :

(2)

где -- заданные «стартовые» значения. Соотношение (2) описывает детерминированный алгоритм, однако при соответствующем подборе преобразования получаемые на его основе псевдослучайные числа по своим функциональным и числовым характеристикам близки к БСВ.

Алгоритмы моделирования вида (2) обладают общим недостатком : начиная с некоторого момента последовательность псевдослучайных чисел образует цикл, который повторяется бесконечное число раз. Длина Т циклически повторяющейся последовательности называется периодом датчика БСВ.

Период Т и коэффициент использования БСВ являются основными показателями качества программных датчиков БСВ. Лучшим датчикам соответствуют большие значения Т и .

В пакете СТАТМОД реализованы два программных датчика БСВ, основанные на мультипликативном конгруэнтном методе и методе Макларена-Марсальи.

Мультипликативный конгруэнтный метод

Согласно этому методу псевдослучайная последовательность реализаций БСВ определяется по рекуррентным формулам :

(3)

где -- параметры датчика (натуральные числа) : -- множитель ( <M), M – модуль, -- стартовое значение (нечётное число).

Операция означает вычет числа по модулю М :

где [ ] – целая часть числа .

Период датчика Т ; коэффициент использования БСВ =1. значения параметров определяются из условия максимума периода Т. значение М зависит от способа представления целых чисел в ЭВМ. Типовые значения параметров :