3.3. Решение системы алгебраических уравнений методом Монте-Карло
Моделирование цепей Маркова оказывается естественным образом связанным с решением большого числа задач, и, в первую очередь, с решением систем линейных алгебраических уравнений.
Рассмотрим простейшую вычислительную схему для решения линейных алгебраических уравнений, которая была впервые предложена Дж. Нейманом и С. Уламом [12].
Пусть система алгебраических уравнений задана в виде
(4.3.1)
где
–
вектор-столбец неизвестных,
– вектор правых частей и
,
– матрица системы.
Предположим, что наибольшее по модулю характеристическое число матрицы А меньше единицы, так что сходиться метод последовательных приближений
,
(4.3.2)
Достаточным
условием для того, чтобы все
характеристические числа матрицы А
лежали внутри единичного круга на
комплексной плоскости, то есть, чтобы
,
,
может служить неравенство
или неравенство
.
Если положить,
что
,
то
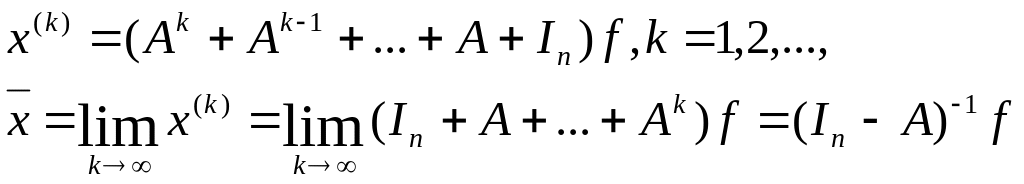(4.3.3)
– точное решение системы (4.3.1)
Рассмотрим
задачу о вычислении скалярного
произведения
,
где h – заданный
вектор.
Мы будем связывать
с системой (4.3.1) и вектором h
некоторую фиксированную цепь Маркова
из множества цепей, определяемых парой
:
, (4.3.4)
,
(4.3.5)
для которых выполнены условия:
,
если
,
,
если
;
(4.3.6)
Положим
(4.3.7)
Зададимся
некоторым целым N ,
и будем рассматривать траектории цепи
Маркова длины N >0.
Объект, переходы которого описываются
цепью Маркова, условимся называть
частицей и считать, что эта частица
изменяет свои состояния (движется в
соответствии с траекторией цепи).
Движущейся частице приписывается "вес"
,
который изменяется при движении ее по
траектории
следующим образом. В начальный момент,
когда она находится в состоянии
, частица имеет вес
,при
переходе из состояния
в состояние
ее вес становиться равным
и т.д., т.е.
.
(4.3.8)
Введем случайную
величину
,
определенную на траекториях Марковской
цепи длины N
,
(4.3.9)
Используя формулу умножения вероятностей, найдем
(4.3.10)
Тогда математическое ожидание СВ равно
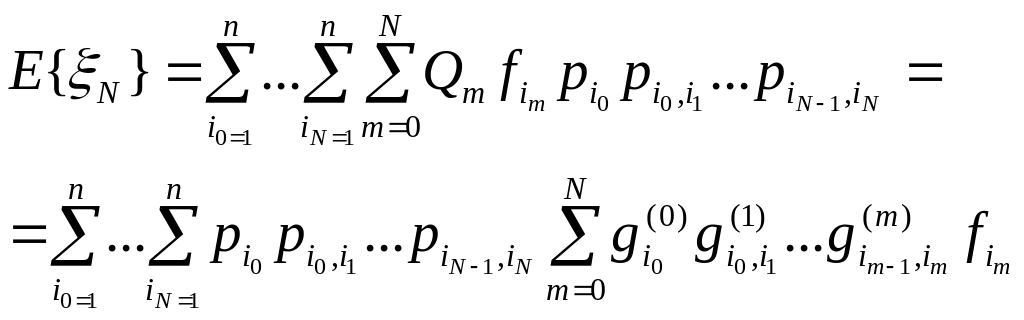(4.3.11)
Подставим
выражения для
,
определяемые по формуле (4.3.7), получим
(4.3.12)
Используя определение произведения матриц получим
, (4.3.13)
т.е.
. (4.3.14)
Из (4.3.3) и (4.3.14)
следует, что при
стремиться к
.
Итак, доказана следующая теорема.
Теорема
4.3.1. Если все характеристические
числа матрицы А по абсолютной величине
меньше единицы, то математическое
ожидание случайной величины
равно
= . (4.3.15)
Для получения
приближенного значения
– j-й компоненты
вектора
(решения системы (4.3.1)) выбираем в качестве
h единичный вектор
,
в котором лишь на j-м
месте стоит единица. Тогда скалярное
произведение (4.3.15) равно
.
Используя результаты (3)
главы, моделируем l
реализаций цепи Маркова:
,
.
(4.3.16)
Вы .16заций
цепи Маркова:)ие ()чения иницы, то
математическое ожидание случайной
величины
согласно формуле (4.3.8), тогда
.
(4.3.17)
Приближенное значение для имеет вид
. (4.3.18)
Пример.
Решить систему линейных алгебраических уравнений с использованием метода Монте-Карло:
Решение:
Приведем систему к виду, при котором применим метод Монте-Карло:
Таким образом, система имеет вид:
Все собственные значения матрицы Ф по модулю меньше 1 и можно применять метод Монте-Карло.
Определим некоторый вектор h следующим образом:
h=
для вычисления x, h=
для вычисления y.
Моделируем вспомогательную цепь Маркова:
,
где
.
Вектор вероятностей начальных состояний
цепи Маркова:
.
Матрица переходных вероятностей имеет
вид:
.
Каждому состоянию цепи Маркова приписываем веса, которые вычисляются по формулам:
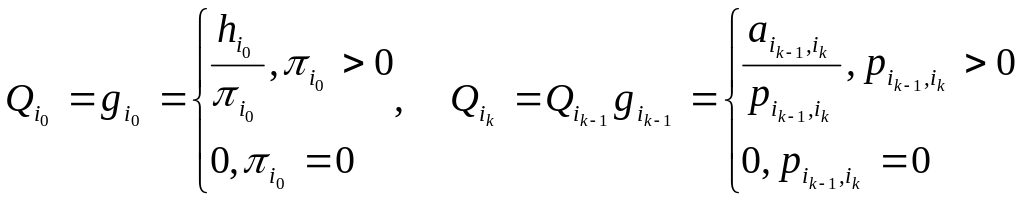
Теперь можем построить СВ
по формуле:
,
где
- номер реализации цепи Маркова. Тогда
приближенное решение вычисляется по
формуле:
или
в
зависимости от вектора h.
Данный алгоритм реализован на языке С++.
Текст программы:
#include <iostream.h>
#include <stdlib.h>
#include <time.h>
void main(){
int n; //Размерность системы
float x=0,y=0; //Решение системы
float **a; //Исходная матрица
float *f; //Правая часть системы
float *h;
float *pi; //Вектор нач. вероятностей цепи Маркова
float **p; //Матрица переходных состояний цепи Маркова
int N; //Длина цепи Маркова
int *i; //Цепь Маркова
float *Q; //Веса состояний цепи Маркова
float *ksi; //СВ
int m; //Количество реализаций цепи Маркова
float alpha; //БСВ
n=2;
a=new float*[n];
for(int k=0;k<n;k++)
a[k]=new float[n];
f=new float[n];
h=new float[n];
pi=new float[n];
p=new float*[n];
for(k=0;k<n;k++)
p[k]=new float[n];
N=1000;
i=new int[N+1];
Q=new float[N+1];
m=10000;
ksi=new float[m];
for(int j=0;j<m;j++)
ksi[j]=0;
a[0][0]=-0.1; a[0][1]=0.8;
a[1][0]=0.4; a[1][1]=-0.1;
f[0]=0.1;
f[1]=-0.2;
h[1]=1;
h[0]=0;
pi[1]=0.5;
pi[0]=0.5;
p[0][0]=0.5; p[0][1]=0.5;
p[1][0]=0.5; p[1][1]=0.5;
//Моделируем m цепей Маркова длины N
for(j=0;j<m;j++)
{
alpha=rand()/float(RAND_MAX);
if(alpha<pi[0]) i[0]=0; //реализуется 1-е состояние
else i[0]=1; //реализуется 2-е состояние
for(k=1;k<=N;k++)
{
alpha=rand()/float(RAND_MAX);
if(alpha<0.5) i[k]=0;
else i[k]=1;
}
//Вычисляем веса цепи Маркова
if(pi[i[0]]>0) Q[0]=h[i[0]]/pi[i[0]];
else Q[0]=0;
for(k=1;k<=N;k++)
{
if(p[i[k-1]][i[k]]>0)
Q[k]=Q[k-1]*a[i[k-1]][i[k]]/p[i[k-1]][i[k]];
else Q[k]=0;
}
for(k=0;k<=N;k++)
ksi[j]=ksi[j]+Q[k]*f[i[k]];
}
for(k=0;k<m;k++)
x=x+ksi[k];
x=x/m;
cout << x;
}
Результат работы программы:
x=-0.0559199
y=-0.199699
Точное решение системы:
x=-5/89≈0.056179775
y=-18/89≈0.202247191