Алгоритмы моделирования:

1. Для целых значений алгоритм моделирования 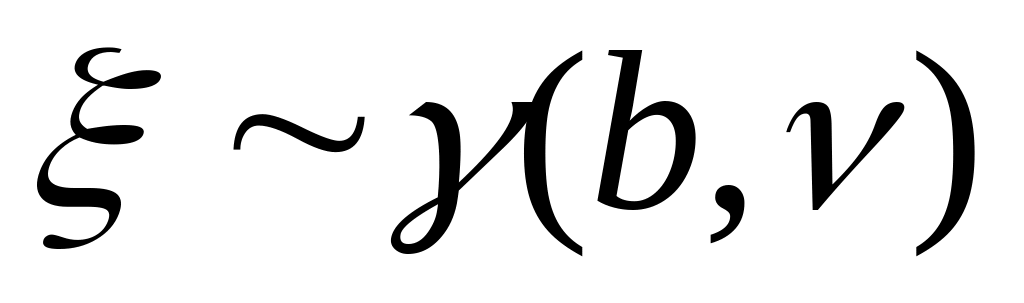описывается формулой (34). Коэффициент использования БСВ .

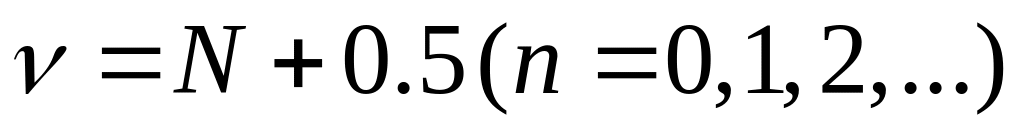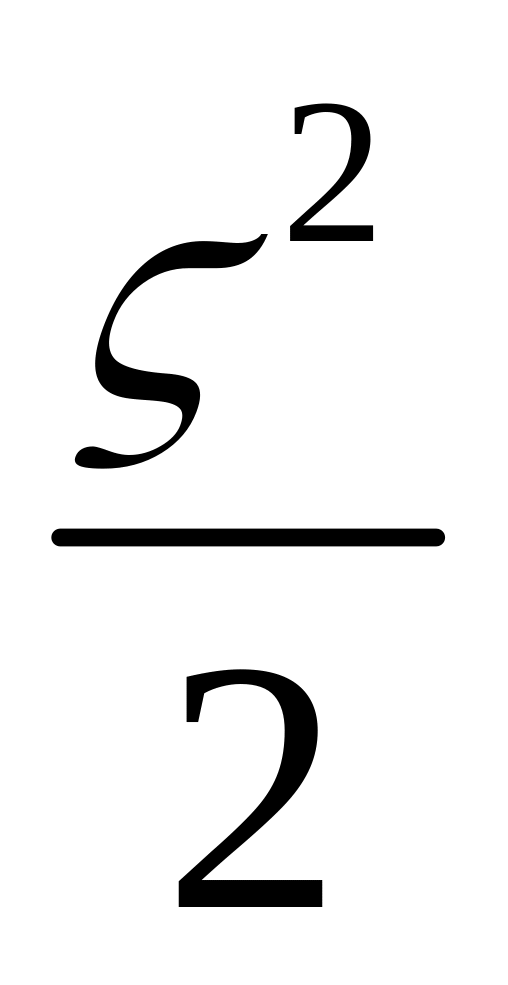2. Для алгоритм моделирования описывается формулой (35). Если для моделирования используется формула (см. «Одномерное нормальное распределение»):

где - независимые БСВ, то коэффициент использования БСВ .

3. Для произвольных значений моделирование СВ может осуществляться с применением алгоритма, основанного на методах исключения и обратной функции.

Справедливо представление (для простоты полагаем ):

где: целая часть числа СВ . Для моделирования используется метод исключения с мажорирующей функцией :

Пусть: и - области, ограниченные осью абсцисс и кривыми и соответственно; - случайный вектор, имеющий равномерное распределение в области , а точка с координатами принадлежит области . Тогда в соответствии с методом исключения реализацией СВ с плотностью является величина . Для моделирования удобно использовать метод обратной функции:

; здесь - независимые реализации БСВ.

Бета-распределение.

НСВ с плотностью распределения

(36)

имеет бета-распределение с параметрами (где - гамма-функция Эйлера).

Среднее значение и дисперсия равны:

Связь с другими распределениями

1. Если 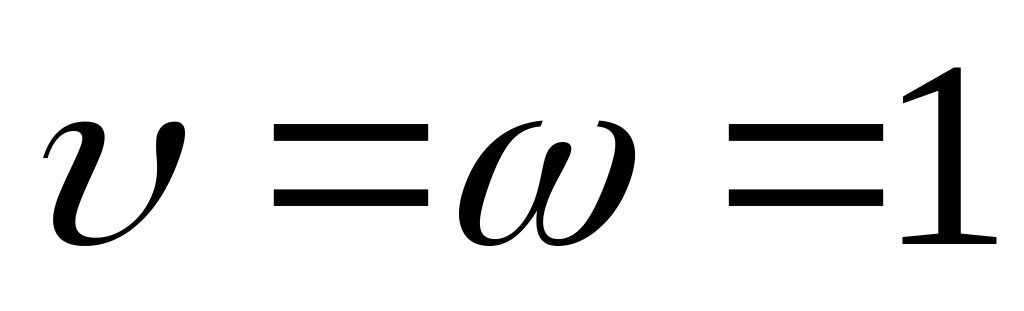, то СВ с плотностью распределения (36) имеет распределение .

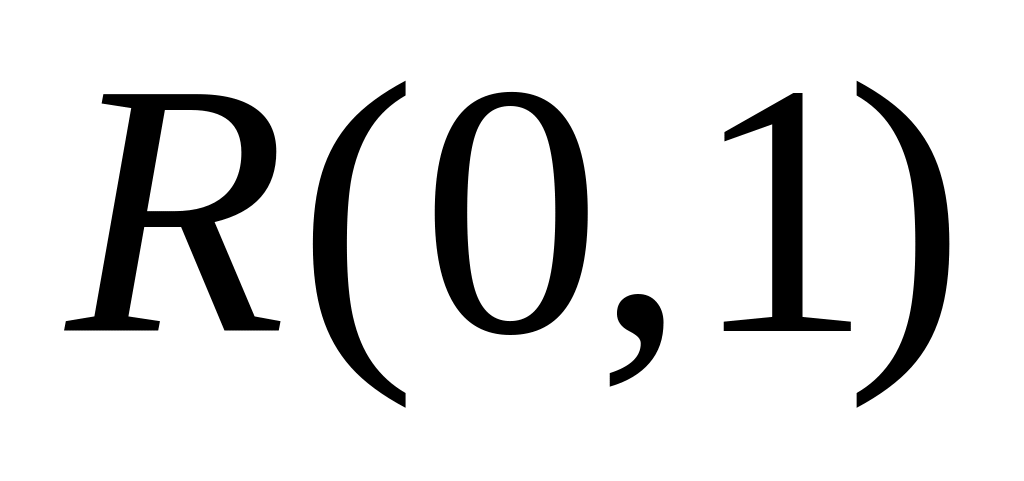2. Если - целые числа, и - случайные величины, имеющие гамма-распределения и соответственно, , тогда:

(37)

Алгоритмы моделирования:

1. Для целых значений алгоритм моделирования определяется формулой (37) (алгоритмы моделирования описаны в разделе «Гамма-распределение»). Коэффициент использования БСВ .

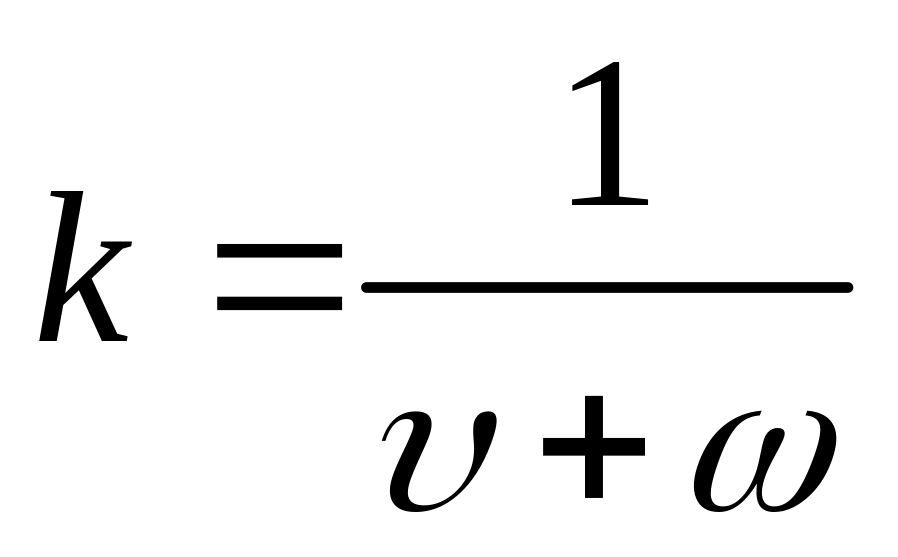2. Другой алгоритм для целочисленных значений параметров основан на методе функционального преобразования и описывается формулой:

где - -я порядковая статистика, соответствующая последовательности независимых БСВ . Коэффициент использования БСВ .

3. Для нецелых параметров используется алгоритм (метод Йонка), составленный из следующих шагов:

4. Моделирование пар независимых реализаций БСВ:

и вычисление величин .

5. Принятие решения о том, что реализацией СВ является величина вида:

где

Распределение Коши.

НСВ с плотностью распределения

(38)

имеет распределение Коши с параметрами: - параметр масштаба; - параметр положения (мода, медиана).

Функция распределения СВ имеет вид:

(39)

Известно, что если - независимые стандартные гаусовские величины, то СВ вида

имеет распределение Коши .

Алгоритмы моделирования

Первый алгоритм основывается на формуле (39) и состоит из двух шагов:

1. моделирование независимых реализаций СВ ;

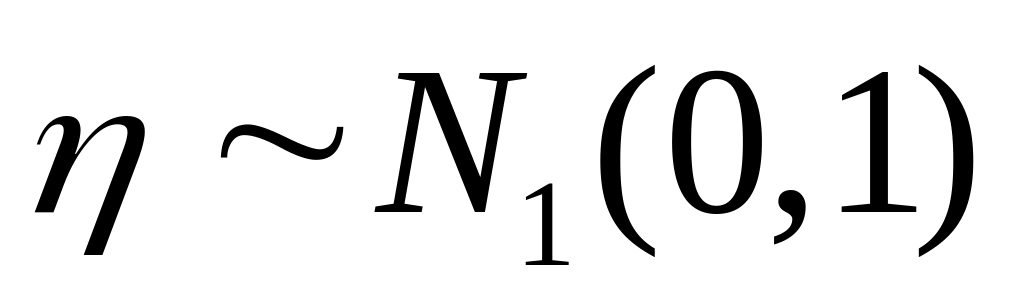2. принятие решения о том, что реализацией СВ является величина :

Коэффициент использования БСВ .

Логистическое распределение

НСВ с плотностью распределения

имеет логистическое распределение с параметрами - среднее значение, (где - стандартное отклонение СВ ).

Функция распределения закона имеет вид:

(40)

Алгоритм моделирования

Алгоритм моделирования основан на методе обратной функции. С учётом (40) обратная для имеет вид:

(41)

Для моделирования реализации СВ выполняются следующие действия.

1. Моделируется реализация 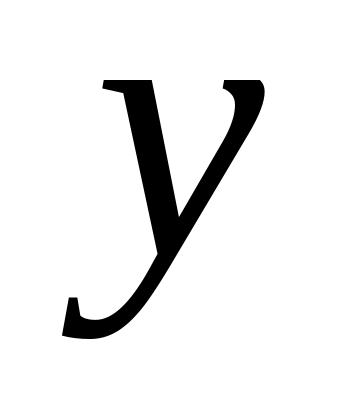БСВ.

2. Вычисляется значение по формуле (41).

Коэффициент использования БСВ .

Хи-квадрат распределение

НСВ с плотностью распределения

(42)

имеет хи-квадрат распределение с степенями свободы ( - натуральное число, параметр распределения). Здесь - гамма-функция Эйлера (см. «Распределение Вейбулла-Гнеленко»).

Среднее значение и дисперсия равны: , .

Известно, что, если - независимые стандартные гаусовские СВ, то СВ

(43)

имеют плотность распределения (42).