Алгоритм моделирования

Алгоритм моделирования ~ основан на методе функциональных преобразований и состоит из следующих шагов:

1. Моделирование z реализации стандартной гаусовской СВ.

2. Получение y реализацией СВ ~ (где ) по формуле: .

3. вычисление реализации x СВ ~ по формуле

.

Экспоненциальное распределение

НСВ с функцией и плотностью распределения, определяемые соотношениями:

, (25)

имеет экспоненциальное(потенциальное) распределение , где -параметр распределения ( ).

Среднее значение и дисперсия СВ равны: .

Связь с другими распределениями

Экспоненциальное распределение можно рассматривать как частный случай распределений:

• гамма - распределения при ;

• Вейбулла-Гнеденко при с=1.

Алгоритм моделирования

Алгоритм моделирования СВ основа на методе обратной функции. Обратная функция для , определяемой (25), находится при решении уравнения относительно x:

.(26)

Далее в соответствии с методом обратной функции алгоритм моделирования СВ состоит из двух шагов:

1. Моделирование реализации a БСВ a.

2. Вычисление в соответствии с (26) реализации x СВ :

где учтено, что a и a-1 одинаково распределены.

Коэффициент использования БСВ к=1.

Распределение Лапласа

НСВ с плотностью распределения

,(27)

имеет распределение Лапласа , где параметр распределения. Распределение иногда называется двусторонним экспоненциальным распределением, поскольку график функции (27) можно рассматривать как результат “склеивания” графика плотности распределении со своим зеркальным относительно вертикальной оси отражением (с учетом необходимой нормировки). Согласно (27) функция распределения имеет вид:

(28)

Среднее значение и дисперсия СВ : .

Алгоритм моделирования

Алгоритм моделирования основан на методе обратной функции. Обратная для функция согласно (28) имеет вид:

(29)

.(30)

Для моделирования реализации x СВ выполняются следующие действия:

1. Моделируется реализация y БСВ.

2. Принимается решение о том, что реализацией СВ является величина x, вычисляемая по формуле (29), если y<0.5; но формуле (30), если .

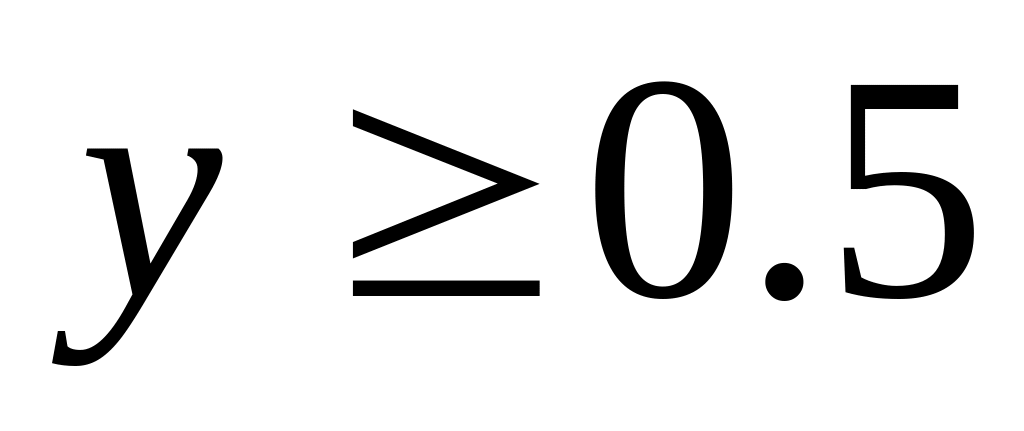Коэффициент использования БСВ к=1.

Распределение Вейбулла-Гнеденко.

НСВ с плотностью распределения

,(31)

имеет распределение Вейбулла-Гнеденко имеет вид:

.(32)

Среднее значение и дисперсия равны:

,

здесь Г(x)-гамма-функция Эйлера, то есть

Связь с другими распределениями

Частными случаями распределения с плотностью (31) являются:

1. экспоненциальное распределение при с=1;

2. распределение Релея, имеющее плотность

при с=2 и .

Алгоритм моделирования

Алгоритм моделирования СВ основан на методе обратной функции с состоит из следующих шагов:

1. Моделирование реализации а БСВ.

2. Принятие решения о том, что реализацией СВ является величина x, вычисляемая с учетом (32) по формуле:

.

Коэффициент использования БСВ к=1.

Гамма-распределение.

НСВ с плотностью распределения

,

имеет гамма-распределение с параметрами: - параметр формы; b>0 – параметр масштаба. Здесь -гамма-функция Эйлера:

Среднее значение и дисперсия равны:

Связь с другими распределениями.

При гамма-распределение совпадает с экспоненциальным: .

Для произвольного целого гамма-распределение называется распределением Эрланга порядка с параметром .

Если -целое число, -независимые случайные величины, распределенные по стандартному экспоненциальному закону , то СВ вида:

(33)

имеет распределение .

В соответствии с методом обратной функции:

(33)

- независимые БСВ. С учётом этого из (33) следует:

(34)

Если - независимые БСВ, , то СВ вида:

(35)

имеет распределение .