
- •Вопросы категории 1. Что в разделе «…» обозначается как «…»?
- •Раздел 1. Основные понятия, гипотезы и принципы.
- •Раздел 2. Растяжение и сжатие.
- •Раздел 3. Механические свойства конструкционных материалов.
- •Раздел 4. Геометрические характеристики плоских сечений.
- •Раздел 5. Сдвиг. Кручение.
- •Раздел 6. Изгиб прямого стержня.
- •Раздел 7. Перемещения при изгибе.
- •Раздел 8. Основы теории напряжённого и деформированного состояния в точке тела.
- •Раздел 9. Сложные виды сопротивления
- •Раздел 10. Усталостная прочность материалов.
- •Раздел 11. Устойчивость сжатых стержней.
- •Вопросы категории 2. Сформулируйте следующее понятие (при необходимости дополните свой ответ формулами, схемами или примерами).
- •Раздел 1. Основные понятия, гипотезы и принципы.
- •Какие виды деформации бруса определяют внутренние силовые факторы ?
- •Раздел 2. Растяжение и сжатие.
- •Раздел 3. Механические свойства конструкционных материалов
- •Раздел 4. Геометрические характеристики плоских сечений.
- •Раздел 5. Сдвиг. Кручение.
- •Раздел 6. Изгиб прямого сечения.
- •Раздел 7. Перемещения при изгибе.
- •Раздел 8. Основы теории напряжённого и деформированного состояния в точке.
- •Раздел 9. Сложные виды сопротивления.
- •Раздел 10. Усталостная прочность материалов.
- •Раздел 11. Устойчивость сжатых стержней.
- •Вопросы категории 3. Выведите зависимости, описывающие…
- •Раздел 1. Основные понятия, гипотезы и принципы.
- •Раздел 2. Растяжение и сжатие.
- •Раздел 3. Механические свойства конструкционных материалов.
- •Раздел 4. Геометрические характеристики плоских сечений.
- •Раздел 5. Сдвиг. Кручение.
- •Раздел 5. Изгиб прямого стержня.
- •Раздел 7. Перемещения при изгибе
- •Раздел 8. Основы теории напряженного и деформированного состояния в точке
- •Плоское напряженное состояние
- •Объёмная деформация
- •Раздел 9. Сложные виды сопротивления
- •Раздел 10. Усталостная прочность материалов
- •Раздел 11. Устойчивость сжатых стержней
- •Дать определение основным видам изгиба.
- •Какие внутренние силовые факторы возникают в сечении бруса при деформации изгиба ?
- •Назвать геометрические характеристики плоских сечений и их размерности.
- •Геометрические характеристики плоских сечений
Вопросы категории 3. Выведите зависимости, описывающие…
Раздел 1. Основные понятия, гипотезы и принципы.
Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

Надо рассечь брус, находящийся в равновесии, на две части и рассмотреть равновесие одной из них.

Действие
усилий отброшенной части бруса заменим
уравновешивающими рассматриваемую
часть внутренней силой
 и внутренним моментом
и внутренним моментом
 .
.

Для
упрощения расчётов силу
 и момент
и момент
 принято раскладывать на составляющие
усилия относительно осей координат
принято раскладывать на составляющие
усилия относительно осей координат
 ,
,
 и
и
 .
.

Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:
-
 – продольная
сила;
– продольная
сила; -
 –
крутящий
(скручивающий) момент;
–
крутящий
(скручивающий) момент; -
 ,
,  – поперечные силы;
– поперечные силы; -
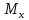 ,
,
 – изгибающие моменты.
– изгибающие моменты.
Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части.
При поперечном изгибе в сечении стержня одновременно возникают поперечная сила и изгибающий момент

Деформация
– это геометрическое искажение в
окрестности материальной точки.
Деформация тоже подразделяется на
линейную и угловую. Для определения
деформации в точке
 рассмотрим два малых отрезка
рассмотрим два малых отрезка
 и
и
 ,
выделенных в теле до его деформации и
после нагружения.
,
выделенных в теле до его деформации и
после нагружения.

После приложения нагрузки отрезки изменяют свою длину и взаимный угол расположения. При этом

будут
являться соответственно линейной и
угловой деформацией в точке
 .
.
Раздел 2. Растяжение и сжатие.
Закон Гука при растяжении и сжатии справедлив лишь в определённых пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Математически закон Гука можно записать в виде равенства:
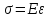 .
.
Коэффициент
пропорциональности  характеризует
жёсткость материала, т. е. его
способность сопротивляться упругим
деформациям растяжения или сжатия, и
называется модулем
продольной упругости
или модулем
упругости первого рода.
характеризует
жёсткость материала, т. е. его
способность сопротивляться упругим
деформациям растяжения или сжатия, и
называется модулем
продольной упругости
или модулем
упругости первого рода.
Если в формулу закона Гука подставим выражения


то получим
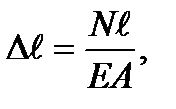
Произведение  , стоящее
в знаменателе, называется жёсткостью
сечения
при растяжении и сжатии; оно характеризует
одновременно физико-механические
свойства материала и геометрические
размеры поперечного сечения бруса.
, стоящее
в знаменателе, называется жёсткостью
сечения
при растяжении и сжатии; оно характеризует
одновременно физико-механические
свойства материала и геометрические
размеры поперечного сечения бруса.
Для бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, продольной силой, изменение длины всего бруса равно алгебраической сумме удлинений и укорочений отдельных участков:
![]()
Линейная деформация (деформация растяжения) – деформация, при которой происходит изменение только одного линейного размера тела.
Количественно
она характеризуется абсолютным
 и относительным
и относительным
 удлинением.
удлинением.
![]()
где
 – абсолютное удлинение;
– абсолютное удлинение;
 и
и
 –
конечная и начальная длина тела.
–
конечная и начальная длина тела.
![]()
![]()
где
 – относительное удлинение тела;
– относительное удлинение тела;
 – абсолютное удлинение тела;
– абсолютное удлинение тела;
 –начальная
длина тела.
–начальная
длина тела.
При
продольном осевом нагружении
(растяжении-сжатии)
в поперечных сечениях бруса имеют
место только нормальные
напряжения  .
.
Поэтому для обеспечения прочности стержней и стержневых систем достаточно выполнение условия:
![]()

 –
коэффициент
запаса прочности, устанавливаемый
нормативными документами.
–
коэффициент
запаса прочности, устанавливаемый
нормативными документами.
