6. Қарапайым дифференциалдық теңдеулерді енгізілген функциялар арқылы шешу.

Дифференциалдық теңдеулер – бір немесе бірнеше белгісіз айнымалы функциясы бар теңдеулер. Егер теңдеуде бір айнымалыдан тәуелді туынды болса, онда ол қарапайым дифференцицалдық теңдеулер болып табылады.

Дифференциалдық теңдеулерді шешу – оның айнымалысының берілген интервалында белгісіз функцияны табу. Теңдеулермен бірге бастапқы шарты беріледі.

MathCad-та қарапайым дифференциалдық теңдеулерді әртүрлі әдіспен шешетін он үш енгізілген функциялар бар. Олардың көпшілігі дифференциалдық теңдеудің бірінші ретті жүйесі түрінде қажет етеді.

MathCad көмегімен бастапқы шарттары және іздейтін функциялары берілген Коши есебін шешуге болады. Көп жағдайда бірінші ретті дифференцицалдық теңдеулерді келесі түрде жазуға болады:

, (1)

(1) теңдеумен қатар бастапқы шарт, яғни қандай да бір t₀ нүктесіндегі у(t₀) функциясының мәні белгілі болу керек. Сондықтан [t₀, t] интервалы арасындағы у(t) функциясын табу керек.

MathCad-та енгізілген функциясының ішінде дифференциалдық теңдеуді шешетін тұрақты қадамды Рунге Кутта әдісі бар. Ол мына түрде жазылады: rkfixed( v,x₀,x_k,n,F). Мұнда v вектор түрінде жазылган бастапқы шарт, x₀, x_k – аргументтің бастапқы және ақырғы мәні, n- қадам саны, F- вектор түрінде жазылған жүйенің оң жақ бөлігі. Осы әдістің шешімі қадамды автоматты түрде таңдаумен болуы мүмкін. Ол үшін мына функция қызмет көрсетеді rkadapt(y, x1, x2, n points, D). Бұл әдістер дифференциалдық теңдеуді бірінші ретті теңдеулер жүйесіне келтіруді қажет етеді.

MathCad-тың соңғы версиясында теңдеулер жүйесін басқа түрге түрлендірмей шеше алатын odesolve(х, b) (ordinary differential equation solution – қарапайым дифференциалдық теңдеулерді шешу) функциясы пайда болды. Бұндағы жақша ішіндегі х – интегралдау айнымалысы, b- аргументтің өзгеруінің жоғарғы шекарасы. Төменгі шекарасы нөлге тең.

Дифференциалдық теңдеулерді шешу үшін Given/Odesolve блогы немесе енгізілген функциясы қолданылады. Given/Odesolve есептеу блогы бір қарапайым диффренциалдық теңдеуді Рунге-Кутта әдісімен шешу қарастырады және үш бөлімнен тұрады:

1) Given кілтті сөзінен;

2) дифференциалдық теңдеу мен логикалық оператор көмегімен жазылған бастапқы

шарттан у(t₀)=b;

3) Odesolve(t,t₁) – [t₀, t] интервалында t айнымалысына қатысты ҚДТ шешу үшін енгізілген функция.

7. 19. Алгебралық теңдеулерді және теңдеулер жүйесін шешу, теңдеу түбірлерін табу. Lsolve, root(), polyroots арнайы функциясын қолдану

MathCad –та теңдеу түбірлерін сандық түрде іздеу үшін root енгізілген функциясы қолданылады. Ол f(x)=0 түріндегі функцияны шешуге мүмкіндік береді, мұндағы f(x)- түбірін табу керек теңдеу, х – белгісіз. root енгізілген функциясын қолданғанда бастапқы жуықтауды беруді керек етеді.

Polyroot функциясы теңдеудің барлық түбірін беретін векторды қайтарады. Теңдеу коэффициенттерін v векторы көмегімен беріледі. v векторының коэффициенттері теңдеудегі дәреженің өсу ретімен орналасады.

Теңдеуді символдық түрде де шешуге болады. Ол үшін Symbolіc/Varіable/Solve менюін шақыру керек. Теңдеу түбірлерін вектор түрінде шығару керек.

Сонымен қатар теңдеуді графиктік түрде шығаруға болады. Графикті түрде шешу теңдеудің сол жағы сипаттайтын функцияның қандай мәнінде теңдеудің оң жағына тең болатын функциянының графигі арқылы анықтау болып табылады.

Сызықты алгебалық теңдеулер жүйесін шешу әдістерінің барлығы екі негізгі топқа бөлінеді: тура (Крамер әдісі, Гаусс әдісі) және итерациялық әдістер. Тура әдістерде есептеулерді сандық түрде де, символдық түрде де шешуге болады. Итерациялық әдістер тек сандық әдістер көмегімен шешуге болады.

Сызықты және сызықты емес теңдеулерді шешу үшін gіven кілтті cөзінен басталып, fіnd функциясын шақырумен аяқталатын «шешу блоктары» қолданылады. Олардың арасында теңдеудің түрі жазылады. Ол жерде теңдік белгісінің орнына Evaluatіon панелінен = белгісін қою керек.

Теңдеудің барлық белгісіздеріне бастапқы жуықтау меншіктелуі керек. Функцияның аргументі ретінде табу керек белгісіздерді жазу керек.

Сызықты емес теңдеулер жүйесінің шешімін lsolve(А,b) енгізілген функция көмегімен тапқанда, шешім ретінде вектор қайтарады. А матрицасы – квадратты матрица, b – теңдеудің оң жағын сипаттайтын вектор.

MathCad символдық процессор көмегімен solve операторын қолданып, теңдеулер жүйесінің аналитикалық шешімін алуға болады. Бұл жағдайда жүйе оператордың сол жақ маркеріне ветор түрінде кіргізіледі, ал ізделіненетін айнымалы solve операторының оң жақ бөлігіне жазылады. Жауап матрица түрінде қайтарылады.

Аналитикалық шешімді gіven кілтті сөзінен басталатын «шешу блоктары» көмегімен де табуға болады.

Теңдеулер жүйесінің жуық шешімдерін mіnerr( x1,...) енгізілген функциясын қолданып табуға болады. Бұл функция өзінің жұмысы бойынша fіnd функциясына ұқсас, бірақ шешімді іздеудің итерациялық процесін аяқтау үшін басқа шарртары болады. Mіnerr функциясын fіnd функциясы шешімді таппаған жағдайда қолдануға мүмкіндік береді.

8. Математикалық физиканың теңдеулерін сипаттайтын физикалық есептерді сандық әдістер көмегімен шешу.

Табиғатта және техникада өте көп таралған құбылыстардың бірі әр түрлі тербелістер. Негізінен тербелістер толқындық теңдеулермен сипатталады. Сондықтан оларды шешу қазіргі кездегі ең маңызды мәселе ьолып табылады.

Біз келесі түрдегі толқындық теңдеуді қарастырамыз:

(15.1)

мұндағы ( уақыт мезетіндегі ішектің тартылуы). Ішектің көлденен тербелісі үшін ізделінетін функциясы уақыттағы ішектің орналасу орнын сипаттайды. Бізге алғашқы және шекаралық шарттар келесі түрде берілсін:

(15.2)

(15.1)-( 15.2) есептерін шешу үшін қарапайым айырымдық схеманың бір үлгінің бір түрі крест үлгісін пайдаланамыз. (15.1) теңдеуіндегі ізделінетін функциясының және бойынша екінші туындыларын түйініндегі тордық функцияның көмегімен шеткі-айырымдық қатынастарға ауыстырамыз:

(15.3)

Бұл жердегі -ші қабаттағы тордық функцияның шамасы үшін айқын өрнек алуға болады:

(15.4)

(15.4) –ші теңдеуде көрсетілгендей, -ші қабаттағы белгісіз шамаларды анықтау үшін және -ші қабаттардағы шешімдерді білуіміз керек. Сондықтан (15.4) –ші формула бойынша есептеу тек екінші қабаттан бастап жргізіледі, ал нөлінші және бірінші қабаттар үшін есептің шешімін алғашқы шарттан анықтаймыз.

Біз нөлдік қабат үшін үшін келесі өрнекті аламыз:

(15.5)

Бірінші қабаттағы шешеімді алу үшін екінші алғашқы шартты пайдаланамыз. Уақыт бойынша алынған бірінші туындыны шеткі-айырымдық аппроксимациямен алмастырамы:

(15.6)

Бұл өрнектен бірінші уақыт қабатындағы тордық функцияның шамасын табамыз:

(15.7)

Жылуөткізгіштік теңдеуді үшін аралас есепті қарастырамыз.

(15.8)

теңдеуін және қанағаттандыратын функциясын табу керек.

Бастапқы шарт

, (15.9)

және шекаралық шарттар

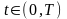, . (15.10)

берілген.

Есепті шешу үшін тор әдісін қолданамыз. Әдістің негізінетуындының н әндерін шекті-айырымды қатынаспен алмастыру жатыр. Тәуелсіз екі айнымалы бар жағдайды қарастырамыз. А йталық хОу жазықтығында шекарасымен қандай да бір облысы берілсін (Сурет 1).

Сурет 1

Жазықтықта екі паралель түзулер жиынтығын қарастырамыз:

, , i=0,1,2,…, k=0,1,2,…

Осы түзулердің қиылысқан нүктелерін түйіндер деп атайды.

Іздеп отырған и=и(х,у) функцияның мәндері тор түйіндерінде деп белгілейік. Әр ішкі түйіндердегі дербес туындыны шекті айырым қатынастары арқылы алмастырамыз:

Шекаралық нүктелерде келесі түрдегі формуланы қолданамыз

, .

Екінші ретті дербес туынды да сәйкесінше алмастырылады

Енді түріндегі теңдеуден келесі теңдеуге көшеміз

- =0.

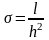деп алып, ішкі түйіндер үшін есептеуге арналған теңдеуді аламыз

(15.11)

болғанда (15.11) теңдеулері орнықты болады. болған кезде (15.9) теңдеуі мына түрде жазылады

(15.12)

Айталық (x,t) – (15.8)-(15.10) есептің шешімі болсын, – дәл мәннің тор әдісімен есептелген мәннен ауытқуы. Онда есептеу қателігі келесі формуламен есептелу керек

, (15.13)

мұндағы = ,