Линейные уравнения 2-го порядка. Классификация

В уравнениях математической физики неизвестным является функция двух и более переменных – обозначим её , частные производные которой входят в уравнение вместе с ней. Порядком уравнения называется наивысший порядок частной производной, входящей в уравнение.

В самом общем случае ДУ¹ в частных производных 2-го порядка с двумя независимыми переменными записывается в виде:

(2.5)

или, пользуясь обозначениями:

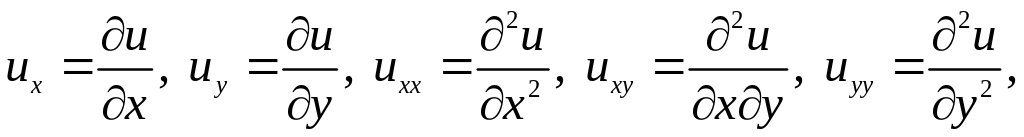
в виде:

(2.6)

Уравнение называется линейным относительно старших производных, если оно имеет вид:

(2.7)

где коэффициенты являются функциями только независимых переменных:

Уравнение называется линейным, если оно линейно как относительно старших производных , так и относительно самой функции и её первых производных то есть имеет вид:

(2.8)

где все коэффициенты являются функциями только независимых переменных:

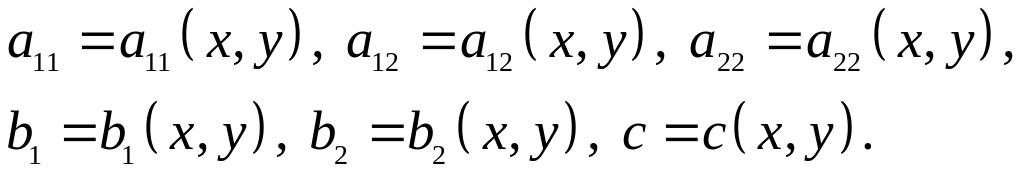
Уравнение (2.7)

называется в точке уравнением:

1. гиперболического типа, если в точке

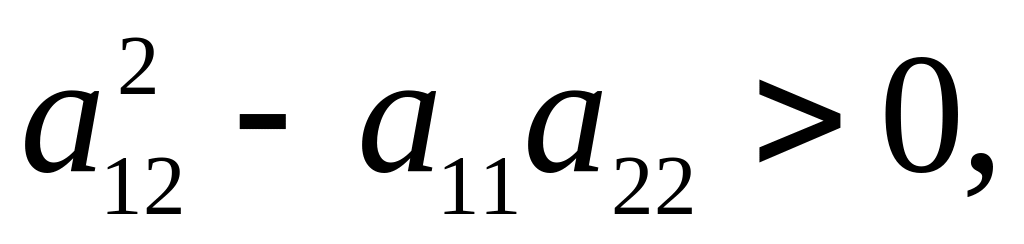
2. эллиптического типа, если в точке

3. параболического типа, если в точке

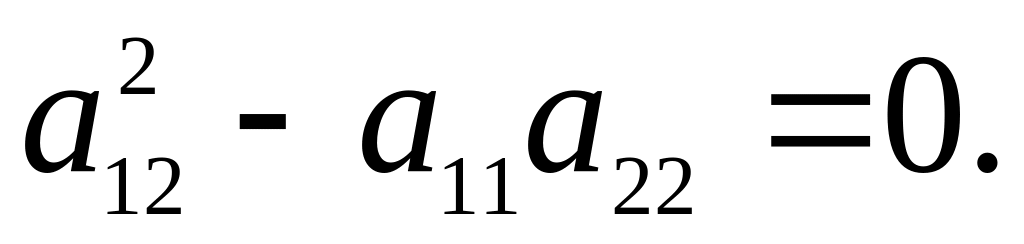
Волновое уравнение относится к уравнениям гиперболического типа.

Уравнение теплопроводности относится к уравнениям параболического типа.

Уравнения Пуассона и Лапласа относятся к уравнениям эллиптического типа.

Основы теории теплопроводности

Как и всякое физическое явление, процесс теплопередачи происходит в пространстве и времени. Поэтому аналитическое исследование теплопроводности сводится к изучению пространственно-временного изменения основной физической величины – температуры, характеризующей данное явление, то есть к нахождению зависимости:

(2.9)

где – время;

– пространственные координаты в декартовой системе отсчёта.

Совокупность точек изучаемого пространства (или тела), для которых в каждый момент времени определена температура, называется температурным полем. Поскольку температура скалярная величина, то температурное поле является скалярным полем.

Различают стационарное и нестационарные температурные поля.

Нестационарное температурное поле – это поле, температура которого изменяется не только в пространстве, но и во времени. Другими словами, в этом случае температура есть функция пространства и времени. Уравнение(2.9) есть математическая запись нестационарного (зависящего от времени) температурного поля.

Стационарное температурное поле – это поле, температура которого в любой точке не изменяется во времени, то есть является функцией только пространственных координат (установившееся состояние):

(2.10)

Температурное поле, соответствующее уравнению (2.9) или (2.10) называется трёхмерным, так как зависит от трёх пространственных координат. Если температура является функцией двух пространственных координат

или

то температурное поле называется двумерным. Если температура – функция одной пространственной координаты

или

то поле называется одномерным. Множество точек поля, имеющих одинаковую температуру образуют изотермическую поверхность. В любой точке такой поверхности

Пересечение изотермической поверхности с плоскостью представляет собой семейство изотерм — линий, соответствующих одинаковой температуре. Если вдоль всякой изотермы температура постоянна, то в любом другом направлении она изменяется. Наибольший перепад температуры на единицу длины происходит в направлении нормали к изотермической поверхности. Вектор, характеризующий возрастание температуры в направлении нормали к изотермической поверхности называется градиентом температуры и равен:

(2.11)

где – единичный вектор нормали к изотермической поверхности, направленный в сторону возрастания температуры;

– производная температуры по направлению нормального вектора к изотермической поверхности в фиксированной точке этой поверхности.

Для обозначения градиента также применяется символ (набла). В виде суммы составляющих вектор градиента температуры выражается формулой:

(2.12)

где и – ортогональные единичные орты координатных осей, которые обычно обозначаются как и соответственно. В этом случае формула градиента принимает вид:

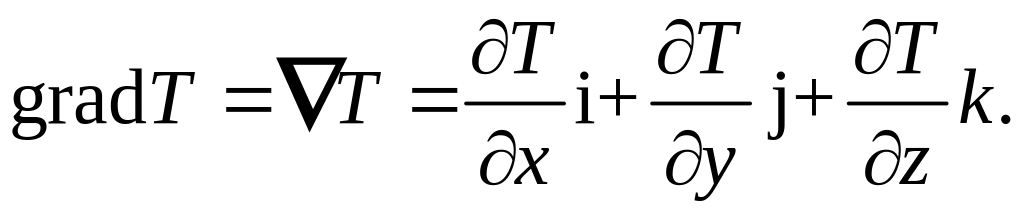
Вектор

(2.13)

называется вектором напряжённости температурного поля.