Доверительные интервалы для генеральной дисперсии и генерального среднего квадратического отклонения

Малые выборки(n 30). Требуется найти доверительный интервал для неизвестной дисперсии нормально распределенной случайной величины ξ, если не известно ее математическое ожидание. Составим для оценку (исправленную выборочную дисперсию). Можно доказать, что случайная величина имеет распределение с n–1 степенями свободы. Тогда,

и ,

т.е. – доверительный интервал для неизвестной дисперсии , причем нижнюю и верхнюю границы интервала находят по таблицам распределения для условий

.

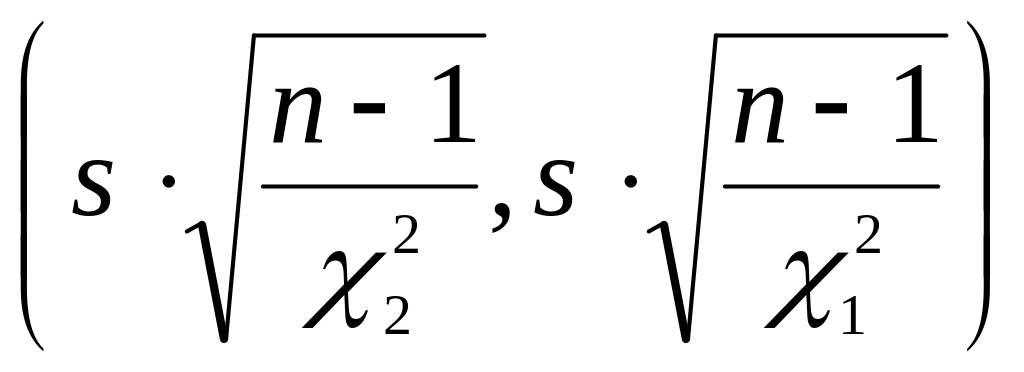– доверительный интервал для неизвестного среднего квадратического отклонения .

Большие выборки (n>30). При выборках достаточно большого объема границы доверительного интервала для генерального среднего квадратического отклонения можно определить по формуле

, где -выборочное среднее квадратическое отклонение; -нормированное значение нормальной случайной величины, соответствующее доверительной вероятности :

Компьютерная часть

Часть 1 Доверительный интервал для математического ожидания a нормального распределения.

Задание 1.

a) Дисперсия известна.

Произведено 5 независимых наблюдений над случайной величиной, распределенной по нормальному закону. Результаты наблюдений таковы:

. Построить доверительный интервал для оценки неизвестного математического ожидания, если =20 и задана доверительная вероятность =0.95.

Решение.

Найдем выборочное среднее xv:

n:=5

xv:=

xv=4

Зададим доверительную вероятность:

Найдем квантиль стандартного нормального распределения(a=0, =1):

u=1.96

Найдем границы доверительного интервала для оценки математического ожидания при известной дисперсии:

aleft:=

aleft= -13.53

aright:=

aright= 21.53

б) Дисперсия неизвестна.

Из нормальной генеральной совокупности извлечена выборка объема n=12:

	-0.5	-0.4	-0.2	0	0.2	0.6	0.8	1	1.2	1.5
	1	2	1	1	1	1	1	1	2	1

Найти доверительный интервал для оценки неизвестного математического ожидания с доверительной вероятностью =0.95.

Решение.

Зададим выборку:

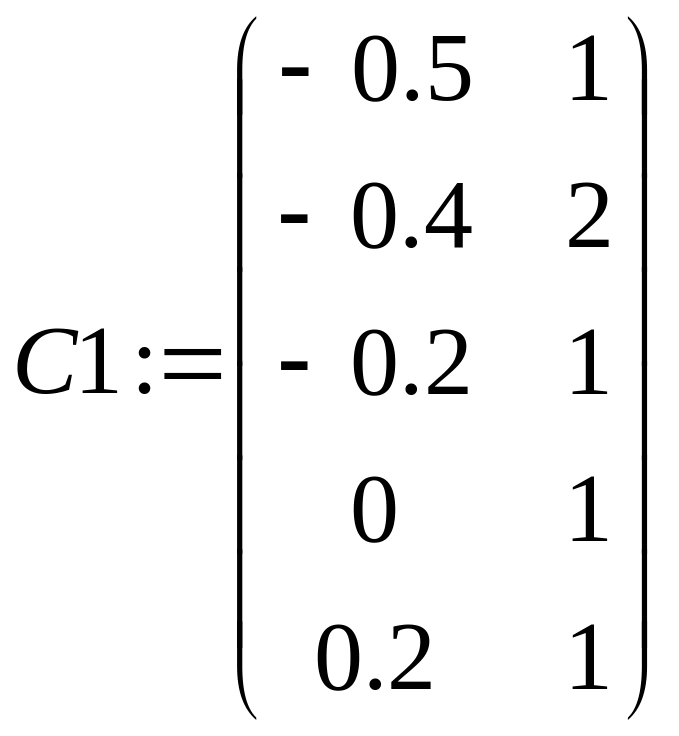
C:=stack(C1,C2).

Найдем выборочное среднее xv и исправленную выборочную дисперсию S2:

ORIGIN:=1

n:=

n=12

xv:=

xv=0.417

S2:=

S2=0.518

Зададим доверительную вероятность:

Найдем квантиль распределения Стьюдента.

k:= n–1 – число степеней свободы

t=2.201

Найдем границы доверительного интервала для оценки математического ожидания при неизвестной дисперсии:

aleft:=

aleft=-0.041

aright:=

aright=0.874

Задание 2.

Дисперсия неизвестна.

Имитация нормально распределенных результатов измерений при помощи генератора случайных чисел.

Сгенерировать выборку нормально распределенных случайных чисел. Найти доверительный интервал для оценки неизвестного математического ожидания с доверительной вероятностью =0.99.

Решение.

Зададим объем выборки:

n:=100

Зададим параметры нормального распределения (они предполагаются неизвестными, служат только для имитации выборки):

µ:=16

σ:=0.25

Создадим выборку из n нормально распределенных случайных чисел:

x:=rnorm(n, µ, σ)

x=

Найдем выборочное среднее xv:

xv:=mean(x) xv= 15.962

Найдем исправленное среднее квадратическое отклонение:

S:= stdev(x) S=0.246

Зададим доверительную вероятность:

Найдем квантиль распределения Стьюдента.

k:= n–1-число степеней свободы

t=2.626

Найдем границы доверительного интервала для оценки математического ожидания при неизвестной дисперсии:

aleft:=

aleft=15.898

aright:=

aright=16.027