Министерство образования Республики Беларусь

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Инженерная математика»

МАТЕМАТИКА

Лабораторный практикум

для студентов

механико-технологического факультета

В 2 частях

Часть 2

М и н с к 2 0 1 3

УДК

ББК

С о с т а в и т е л и :

Бокуть Л.В., Прихач Н.К., Пикман Ю.А., Глинская Е.А., Прусова И.В., Реутская О.Г.

Под общей редакцией М.А. Князева

Р е ц е н з е н т ы :

Белорусский национальный технический университет

пр-т Независимости, 65, г. Минск, Республика Беларусь

Тел.(017)292-77-52 факс (017)292-91-37

E-mail: emd@bntu.by

http://www.bntu.by/ru/struktura/facult/psf/chairs/im/

© БНТУ, 2013.

© Коллектив авторов, 2013.

СОДЕРЖАНИЕ

8

Таким образом, получаем элементарную квадратурную формулу средних прямоугольников: 8

Листинг 1.1. 12

12

13

Л а б о р а т о р н а я р а б о т а № 1

Методы численного интегрирования. Формула средних прямоугольников. Формула трапеций. Метод Монте-Карло

Цель работы: освоение методов численного интегрирования в среде MathCAD. Используемые программные средства: MathCAD 14.

Теоретические сведения

Пусть дана непрерывная на отрезке функция Фигура , ограниченная осью , ординатами , где и графиком функции называется кри волинейной трапецией. Она изображена на рис. 1.1.

О пределённый интеграл от функции по отрезку выражает площадь криволинейной трапеции :

, (1.1)

где – площадь фигуры. Фигура, для которой площадь определяется однозначно и имеет конечное значение, называется квадрируемой, а её площадь квадратурой. Поэтому вычисление определённых интегралов также называют квадратурой.

Площадь обладает свойством аддитивности. Это значит, что если какая-либо квадрируемая фигура разбита на несколько частей, составляющих её, то сумма площадей составляющих фигур равна площади всей фигуры:

И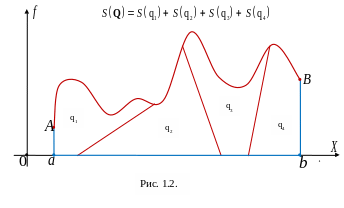 ллюстрация этого факта на рис. 1.2.

Ч исленные методы позволяют найти приближённое значение интеграла, когда известна подынтегральная функция и промежуток интегрирования, не прибегая к нахождению первообразной, и основаны на замене определённого интеграла конечной суммой вида

, (1.2)

где – числовые коэффициенты;

– точки из отрезка ;

– значения подынтегральной функции в точках .

Приближённое равенство

, (1.3)

называется квадратурной формулой, сумма (1.2), аппроксимирующая интеграл – квадратурной суммой; точки – узлами квадратурной формулы, числа – коэффициентами квадратурной формулы. Разность

, (1.4)

определяет погрешность квадратурной формулы и зависит как от расположения узлов, так и от выбора коэффициентов. Множество всех узлов квадратурной формулы называется сеткой. Сетка разбивает исходный промежуток интегрирования на сегменты . Расстояние между двумя соседними узлами называют шагом сетки. Сетка, у которой шаг имеет постоянное значение для любых двух соседних узлов, называется равномерной. Это значит, что все сегменты такого (равномерного) разбиения имеют одинаковую длину.

Равномерная сетка

(1.5)

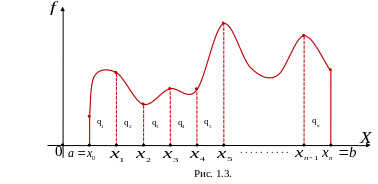
разбивает отрезок ровно на сегментов одинаковой длины и, соответственно, на столько же криволинейных трапеции , которые и составляют исходную фигуру Q (рис. 1.3).

Составляющие криволинейные трапеции будем называть элементарными. Площадь каждой из них также выражается определённым интегралом:

. (1.6)

По свойству аддитивности площадь фигуры представляется в виде суммы площадей элементарных криволинейных трапеций :

. (1.7)

и задача сводится к построению элементарной квадратурной формулы для интеграла:

. (1.8)