Системы линейных алгебраических уравнений.

Системой m линейных алгебраических уравнений (СЛАУ) с n неизвестными будем называть следующую систему:

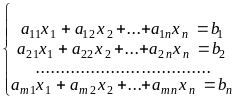
где x_j, j= -неизвестные; а_ij, -коэффициенты при неизвестных; b_i, - свободные члены. При b_i=0, , система называется однородной.

Решением системы называется такая совокупность чисел , которая при подстановке вместо в каждое уравнение системы обращает его в тождество.

СЛАУ называется совместной, если она имеет решение, несовместной - если решения нет

Однородная система всегда совместна, т.к. имеет нулевое решение.

Совместная система называется определенной, если она имеет единственное решение, неопределенной - если решений бесконечное множество.

Две совместные системы называются равносильными, если все их решения совпадают.

Коэффициенты при неизвестных в системе составляют прямоугольную таблицу - матрицу A_mn из m строк и n столбцов, она называется основной матрицей системы, а матрица (А\В) - расширенной:

.

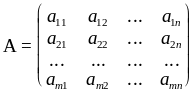
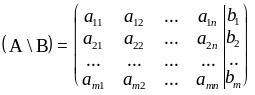Строки и столбцы матрицы можно воспринимать как вектора.

Рангом матрицы А (обозначается rgA) называется максимальное число линейно-независимых строк матрицы.

Теорема Крониккера-Капелли. Система линейных уравнений совместна тогда, когда rang(A)=rang(A\B).

В случае если матрица системы представляет из себя, не вырожденную квадратную матрицу, то возможны три метода ее решения.

Матричный метод.

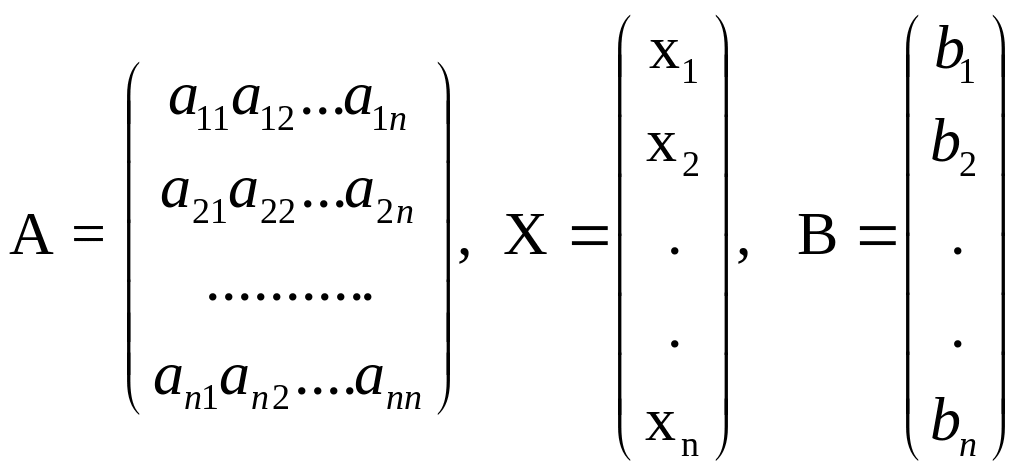
Исходную систему уравнений можно представить в виде , где . Таким образом, вектор столбец переменных представляет из себя произведение обратной матрицы к матрице системы на вектор столбец свободных членов.

Метод Крамера.

Неизвестные системы определяют по формулам: Где  - определитель исходной матрицы системы, а _j определитель получается из определителя  заменой j-го столбца столбцом свободных членов.

Метод Гаусса.

Данный метод заключается в последовательном исключении неизвестных из уравнений системы путем элементарных преобразований над расширенной матрицей.

Процесс продолжаем, пока не получим треугольную матрицу.

Из последней строки определим x_n, зная значение этой переменной из предпоследней строки определим значение x_n-1, …

Данный метод легко обобщаем на случай когда число переменных не равно числу уравнений.

Также при помощи элементарных преобразований приводим расширенную матрицу к ступенчатому виду

(A\B)~ ,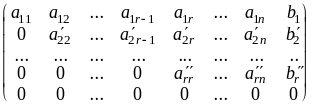

причем rg(A\B) равен числу ненулевых строк в ступенчатой матрице.

Возможны три случая:

1. Получилась строка (0 0 ...0| b_k),b_k0, ей соответствует уравнение

0=b_k - система несовместна (rgA rg(A\B)).

2. Число ненулевых строк r меньше числа неизвестных, тогда система имеет бесчисленное множество решений. Последней ненулевой строке соответствует уравнение a_rrx_r +...+ a_rnx_n=b_r , из которого находим неизвестное x_r через n-r так называемых свободных неизвестных: x_r+1, ...., x_n. Из уравнений, соответствующих другим строкам, последовательно находим x₁, ..., x_r-1 также через свободные неизвестные.

3. r=n - решение системы единственно. Последней ненулевой строке соответствует уравнение a_nnx_n = b_n, из которого находим неизвестное х_n , а далее последовательно - x₁, x₂, ..., x_n-1.