Элементы линейной алгебры и аналитической геометрии Матрицы

Матрицей называется прямоугольная таблица чисел размерности mn. Она кратко записывается в виде А=(а_ij), .

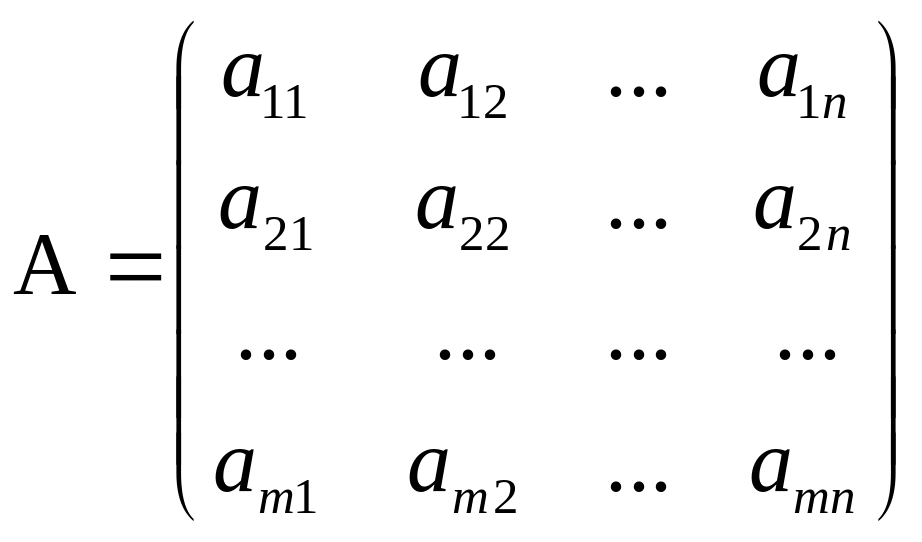
Числа (а_ij) -элементы матрицы; i-номер строки; j-номер столбца.

Две матрицы А=(а_ij), В=(b_ij), одинаковой размерности mn называются равными, если а_ij= b_ij, .

Суммой матриц А=(а_ij), В=(b_ij) одинаковой размерности mn называется матрица С=( а_ij + b_ij), .

Сложение матриц подчиняется законам коммутативности и ассоциативности и сочетательным законам: А + В = В + А, (А + В) + С = А + (В + С).

Матрица, все элементы которой нули, называется нулевой матрицей, обозначается 0. А + 0 =А.

Произведением матрицы А на число  называется матрица В=А=( а_ij), .

Произведением матрицы А=(а_ij) размерности mp на матрицу В=(b_ij) размерности pn (число столбцов матрицы А должно быть равно числу строк матрицы В) называется матрица С=(a_i1b_1j+ ai₂b_2j + ...+ a_ipb_pj), .

Произведение матриц в общем случае не подчиняется коммутативному закону: АВВА.

Для более простого запоминания и понимания правила умножения матриц возможно его восприятия следующим образом: при умножении строка первой матрицы накладывается на столбец второй, все числа наложенные друг на друга перемножаются, а результаты этих произведений складываются между собой.

Таким образом для получения элемента c_ij результирующей матрицы С необходимо i-тую строку матрицы А наложить на j-тый столбец матрицы В.

Для матриц остаются справедливы следующие соотношения:

А(ВС)=(АВ)С, (А + В)С = АС + ВС.

Особый класс среди матриц представляют собой, так называемые квадратные матрицы.

Квадратной матрицей n-ого порядка называется таблица чисел.

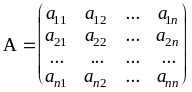
Одной из характеристик квадратной матрицы служит ее определитель (детерминант).

Определителем (детерминантом) II порядка, соответствующим квадратной матрице II порядка, называется число, обозначаемое символом:

и вычисляемое по правилу: произведение элементов лежащих на главной диагонали минус произведение элементов лежащих на дополнительной диагонали =a₁₁ a₂₂ - a₂₁ a₁₂.

Определителем III порядка, соответствующим квадратной матрице III порядка, называется число, вычисляемое по правилу: произведение элементов лежащих на главной диагонали плюс произведение элементов лежащих в углах треугольника с основанием параллельным главной диагонали минус произведение элементов лежащих на дополнительной диагонали и минус произведение элементов лежащих в углах треугольника с основанием параллельным дополнительной диагонали

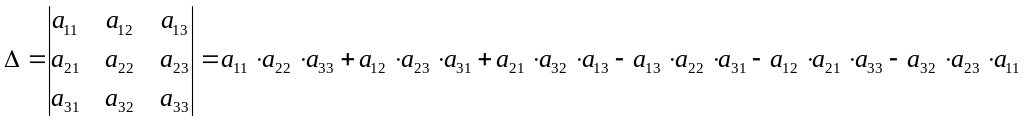
К сожалению, для матриц более высокого порядка таких простых правил вычисления определителя не существует.

Минором М_ij элемента а_ij определителя называется определитель, полученный из данного путем вычеркивания i-ой строки и j-го столбца.

Алгебраическим дополнением А_ij элемента а_ij называется число А^(ij)=(-1)^i+j М_ij

Определителем (детерминантом) матрицы n-ого порядка является число вычисляемое при помощи следующей формулы: . Применение данной формулы при вычислении определителей называют разложением определителя по строке.

Для определителя справедливо выполнение следующих свойств:

1. Определитель равен нулю, если: все элементы какой-нибудь строки равны нулю или соответствующие элементы двух строк пропорциональны.

2. Определитель матрицы равен определителю транспонированной матрицы (матрица транспонируется если в ней поменять местами строки и столбцы)

3. При перестановке двух строк в квадратной матрице определитель меняет знак.

4. Общий множитель всех элементов строки можно вынести за знак определителя.

5. Определитель не изменится, если к одной его строке прибавить другую строку, умноженную на одно число не равное нулю.

На использовании вышеперечисленных свойств основан метод Гаусса вычисления определителя матрицы. Метод Гаусса заключается в том, чтобы используя свойства 3-5 получить из исходной матрицы матрицу треугольную, т.е. такую у которой ниже диагонали нули. Определитель треугольной матрицы равен произведению диагональных элементов (Это не сложно показать, раскладывая определитель каждый раз по последней строке).

Для квадратных матриц одинакового порядка умножение всегда возможно. Особое значение при таком умножении имеет так называемая единичная матрица Е, у которой по главной диагонали стоят единицы, а выше и ниже диагонали - нули:

Очевидно, что определитель единичной матрицы detE=1. Легко проверяется, что АЕ=ЕА=А.

Если матрица С=АВ для квадратных матриц А и В, то detC=detA^.detB. Для квадратной матрицы вводится понятие обратной матрицы.

Матрица А^-1 называется обратной для квадратной матрицы А, если:

АА^-1=А^-1А=Е

Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. detA=0

Нахождение обратной матрицы возможно двумя способами.

1. Способ присоединенной матрицы: по формуле ,

где А^(ij), -алгебраические дополнения элементов a_ij определителя

=detA= .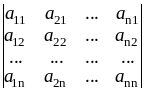

2. Нахождения обратной матрицы методом элементарных преобразований:

Элементарными преобразованиями являются:

а) перестановка двух строк в матрице.

б) умножение или деление всех элементов строки на одно и тоже число .

в) вычитание из одной строки матрицы другой строки умноженной на число .

Записав рядом с исходной квадратной матрицей, через черту, единичную квадратную матрицу того же порядка, и применяя к вновь построенной матрице элементарные преобразования таким образом чтобы на месте исходной матрицы получилась единичная, получим на месте единичной матрицы матрицу обратную к исходной.