8. Теплоотдача при свободном движении жидкости

Задача 8.5 (б)

Вычислить коэффициент теплоотдачи от трубы к воздуху для двух случаев: 1) воздух движется в длинной трубе внутренним диаметром d; 2) воздух омывает трубу наружным диаметром d снаружи в поперечном направлении. В обоих случаях температура воздуха t_в, скорость воздуха принять 5, 12, 20 и 28 м/с. Построить график зависимостей α=ƒ(w) для продольного и поперечного потоков воздуха.

Решение:

Конвективный теплообмен при свободном течении жидкости основан на изменении плотности жидкости при нагревании. В промышленности свободная конвекция широко применяется. Свободная конвекция возникает у нагретых стен котельных агрегатов, печей, батарей отопления, в холодильниках при охлаждении продуктов и т.д.

Если тело имеет более высокую температуру, чем окружающая среда, то слои жидкости, нагреваясь от тела, становятся легче и под действием подъемной силы поднимаются вверх, а на их место приходят более холодные слои. Поэтому возникает свободная конвекция.

Свободное движение жидкости у поверхности тела может быть как ламинарным, так и турбулентным. Характер движения жидкости в основном зависит от температурного напора, т.е. от разности температур стенки объекта и окружающей среды. При малых значениях температурного напора вдоль поверхности наблюдается ламинарное течение.

При больших температурных напорах преобладает турбулентное течение жидкости.

При свободной конвекции форма тела имеет второстепенное значение. Основное значение при свободной конвекции имеет длина поверхности, вдоль которой происходит теплообмен.

При свободной конвекции для определения средних значений коэффициентов теплоотдачи можно пользоваться формулами

При t_ст = соnst Nu_ж = 0,63 ( GrPr )^0,25 2.63

При q_ст = const Nu_ж = 0,75 (Gr_ж Pr_ж)^0,25 ( Pr_ж / Pr_ст)^0,25 2.64

Формулы получены для теплоносителей с числом Рr от 0.7 до 3^.10³ при10³ < Gr Pr < 10⁹.

За определяющую температуру принята температура вдали от нагретой поверхности, за определяющий размер – длина поверхности.

Для определения средних значений коэффициентов теплоотдачи при свободном турбулентном течении жидкости вдоль вертикальной стенки, которое наступает при числах Gr_ж Pr_ж > 6^.10¹⁰ предложена формула

Nu_ж = 0,15 ( Gr_ж Pr_ж )^0,33( Pr_ж/ Pr_cт)^0,25 2.65

Если 10⁹ < Gr_жPr_ж < 6^.10¹⁰, то вдоль вертикальной пластины имеет место переходный режим свободного движения жидкости. Переходный процесс характеризуется неустойчивостью как процесса течения жидкости, так и теплоотдачи.

Для определения средних коэффициентов теплоотдачи при свободном ламинарном движении жидкости около горизонтальных труб при 10³ < Gr_жPr_ж < 10⁸ предложена формула

Nu_ж = 0,5 ( Gr_ж Pr_ж )^0,23( Рr_ж / Рr_ст )^0,25 2.66

В этой формуле за определяющую температуру принята температура капельной жидкости или газа вдали от трубы, а за определяющий размер – диаметр трубы. Около горизонтальных нагретых поверхностей движение жидкости имеет особый характер и зависит от положения и размеров теплоотдающих поверхностей. Если нагретая поверхность обращена кверху, то коэффициент теплоотдачи увеличивается на 30%. Если поверхность обращена книзу, то коэффициент теплоотдачи уменьшается на 30%. При расчете теплоотдачи плит за определяющий размер берется меньшая сторона плиты.

Решение задачи:

Для воздуха при tв=70 °С: υж=20,02*10^-6 м²/с; λж=2,96*10^-2 Вт/м*град;

1) Продольное течение воздуха

Определим число Рейнольдса для каждого значения скорости:

1) Для скорости

=> движение турбулентное

Критерий Нуссельта:

Prж=0,694;

Prc=0,694;

Так же верна формула

Коэффициент теплоотдачи: α1= Nuж*λж = 33,98*2,96*10^-2= 20 Вт/м²*град;

d 50*10^-3

2) Для скорости

=> движение турбулентное

Критерий Нуссельта:

Prж=0,694;

Prc=0,694;

Так же верна формула

Коэффициент теплоотдачи: α2= Nuж*λж = 68,45*2,96*10^-2= 41 Вт/м²*град;

d 50*10^-3

3) Для скорости

=> движение турбулентное

Критерий Нуссельта:

Prж=0,694;

Prc=0,694;

Так же верна формула

Коэффициент теплоотдачи: α3= Nuж*λж = 103*2,96*10^-2= 61 Вт/м²*град;

d 50*10^-3

4) Для скорости

=> движение турбулентное

Критерий Нуссельта:

Prж=0,694;

Prc=0,694;

Так же верна формула

Коэффициент теплоотдачи: α4= Nuж*λж = 134,81*2,96*10^-2= 80 Вт/м²*град;

d 50*10^-3

2) Поперечное омывание воздухом

Определим число Рейнольдса для каждого значения скорости:

1) Для скорости

Критерий Нуссельта:

Prж=0,694;

Prc=0,694;

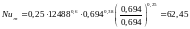
Так же верна формула

Коэффициент теплоотдачи: α1= Nuж*λж = 62,45*2,96*10^-2= 37 Вт/м²*град;

d 50*10^-3

2) Для скорости

Критерий Нуссельта:

Prж=0,694;

Prc=0,694;

Так же верна формула

Коэффициент теплоотдачи: α2= Nuж*λж = 105,6*2,96*10^-2= 63 Вт/м²*град;

d 50*10^-3

3) Для скорости

Критерий Нуссельта:

Prж=0,694;

Prc=0,694;

Так же верна формула

Коэффициент теплоотдачи: α1= Nuж*λж = 143,48*2,96*10^-2= 85 Вт/м²*град;

d 50*10^-3

4) Для скорости

Критерий Нуссельта:

Prж=0,694;

Prc=0,694;

Так же верна формула

Коэффициент теплоотдачи: α2= Nuж*λж = 175,57*2,96*10^-2= 104 Вт/м²*град;

d 50*10^-3

Вывод: При поперечном омывании трубы воздухом значения коэффициента теплоотдачи больше, чем при продольном.

График зависимости коэффициента теплоотдачи от скорости α=f(ω).

Для продольного потока воздуха:

Для поперечного потока воздуха:

Ответ:

Продольное течение воздуха	Поперечное течение воздуха
α1= 20 Вт/м2*град;	α1= 37 Вт/м2*град;
α2= 41 Вт/м2*град;	α2= 63 Вт/м2*град;
α3= 61 Вт/м2*град;	α3= 85 Вт/м2*град;
α4= 80 Вт/м2*град;	α4= 104 Вт/м2*град;