Задание №7.

Заданы отношения:

R:

А1	А2	А3
a	b	C
a	c	d
b	d	a
d	a	b

S:

B1	B2	B3
a	d	b
a	c	d
b	d	a

Записать обозначения операций и выполнить их:

а) селекция отношения Rпо условию «А₂>b»;

б) проекция на список (3, 1) объединения отношений RиS.

Решение:

а) Селекция отношения Rпо условию «А₂>b».

В1	В2	В3
a	c	d
b	d	a

б) проекция на список (3, 1) объединения отношений RиS.

Степень отношения Rравна 3 (3 столбца в таблице), степень отношенияSравна 3 (тоже 3 столбца), значит, отношенияRиSсовместимы и можно над ними выполнять операцию объединения.

Обозначение операции проекции , обозначение операции объединения отношений:

D1	D2	D3
a	b	c
a	c	d
b	d	a
d	a	b
a	d	B

Чтобы выполнить операцию , выписываем третье и первое поле во всех записях в новую таблицу:

С1	С2
с	a
d	a
a	b
b	d
b	a

Задание №8.

Даны множества и. Какова мощность множеств?

Решение

Множество А конечно и задано перечислением своих элементов, множество В задано характеристическим свойством. Запишем несколько первых элементов множества . Видим, что, т.е. оно конечно, и его мощность.

. Покажем, что множество счетно. Занумеруем его элементы:

Задана биекция множества Nна множество. Следовательно,- счетно и.

По определению декартова произведения . Запишем элементы этого множества в виде матрицы и занумеруем их по столбцам:

	1	4	7	10	13	…
-1	(-1, 1)1	(-1, 4)4	(-1, 7)7	(-1, 10)10	(-1, 13)13	…
0	(0, 1)2	(0, 4)5	(0, 7)8	(0, 10)11	(0, 13)14	…
1	(1, 1)3	(1, 4)6	(1, 7)9	(1, 10)12	(1, 13)15	…

Если номер nделится на 3 без остатка, то первый элемент пары равен 1. Если номерnделится на три с остатком 1, то первый элемент пары равен -1. Если номерnделится на 3 с остатком 2, то первый элемент пары равен 0.

Поэтому способ нумерации может быть задан следующим образом:

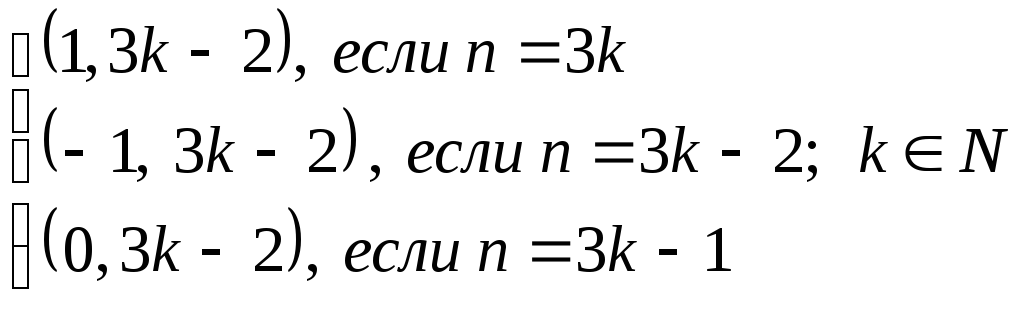
Следовательно, множество счетно и имеет мощностьN₀/

Задание №9.

Равномощны ли множества и?

Решение

Покажем, что множества равномощны по теореме Кантора-Берштейна. Найдется такое , чтоХ₁равномощноУ. И найдется такое, чтоУ₁равномощно Х.

Выберем в качестве Х₁открытое множество. БиекцияХ₁наУлегко устанавливается, например, по закону

В качестве подмножества возьмем любой замкнутый интервал, например,. БиекцияУ₁ наХустанавливается, например по закону:

Таким образом, условия теоремы Кантора-Берштейна выполняются, следовательно, множества иравномощны.