1- 2_Спецглавы математики

Министерство образования

Российской Федерации

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И

РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Автоматизированная система обработки информации и управления.

Контрольная работа №1

по дисциплине «спецглавы математики»

вариант №2.

Студент гр.

Код

Пароль

25.07.2002

2002

Задание №1:

Решить задачу, используя диаграмму Эйлера-Венна.

В туристическом клубе несколько раз за лето организуются походы, причем все члены клуба хотя бы раз в них участвуют. Сорок человек побывали в пеших походах, 28 – в конных, 25 – в лодочных. И в пеших, и в конных походах побывало 20 человек, в пеших и лодочных – 15, в конных и лодочных – 8, во всех видах походов побывало 6 человек. Сколько туристов в клубе?

Решение:

В задаче идет речь о трех множествах П., К, Л – виды походов, пешие, конные, лодочные соответственно. Универсальное множество U – это множество туристов в клубе. Запишем краткое условие задачи:

?

Перенесем эти данные на диаграмму Эйлера – Венна. Запишем сначала элементы множества. Запишем элементы множества , но 6 из них уже учтены, значит, записываем оставшиеся 2. Теперь внесем элементы множества , из которых 6 уже учтены, значит, записываем в это множество оставшиеся 9 элементов. Внесем элементы множества , 6 элементов из них уже учтены, записываем оставшиеся 14. Найдем количество человек побывавших только в конных походах. Всего во множестве из них мы уже учли, значит, только в конных походах побывало 6 человек, записываем 6. Всего во множестве из них мы уже учли, значит, только в пеших походах побывало 11 человек, записываем 11. Всего во множестве из них мы уже учли, значит, только в лодочных походах побывало 8 человек, записываем 8.

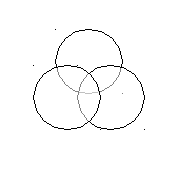
К

6

2 6 14

Л 8 9 11 П.

Ответ: 56 человек – количество туристов в клубе.

Задание №2:

Задано универсальное множество и множества , , . Записать булеан множества Х, любое разбиение множества Y, покрытие множества Z. Выполнить действия

Решение:

Для выполнения действия выполним действия над множествами в порядке:

1)

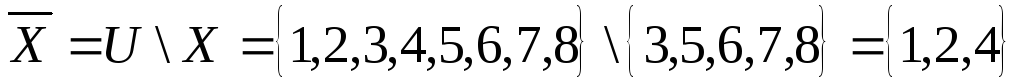
2)

3)

Булеан множества Х

Номер подмножества	Двоичная запись номера	Подмножества множества
0	00000
1	00001
2	00010
3	00011
4	00100
5	00101
6	00110
7	00111
8	01000
9	01001
10	01010
11	01011
12	01100
13	01101
14	01110
15	01111
16	10000
17	10001
18	10010
19	10011
20	10100
21	10101
22	10110
23	10111
24	11000
25	11001
26	11010
27	11011
28	11100
29	11101
30	11110
31	11111

Построим разбиение для множества Y, которое состоит: , ,,

Множества не пусты, не пересекаются. их объединение равно множеству Y: .

Для построения покрытия выберем подмножества . Полученная система множеств состоит из двух блоков, объединение которых равно множеству Z:

.

Задание №3:

Упростить, используя законы и тождества алгебры множеств (перечислить используемые законы):

Решение:

1) (закон дистрибутивности, св-ва универсального множества).

2) (закон ассоциативности, св-ва универсального множества)

Задание №4:

Пользуясь только определениями операций над множествами и определением равенства множеств, доказать:

Доказательство:

называется пересечением множества, состоящее из тех и только тех элементов, которые принадлежат одновременно и множеству А, и множеству В.

называется объединением множества, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств.

Обозначим левую часть через x, правую через y. Согласно определению равенства множеств покажем, что выполняются условия одновременно.

Пусть , тогда по определению объединения множеств . Значит,отсюда следует, что

Задание №5:

Пусть Отношение задано характеристическим свойством:

Задать отношение другими возможными способами. Выяснить, какими свойствами оно обладает.

Решение:

Отношение R можно задать перечислением всех элементов:

Отношение R можно представить с помощью графика и графа:

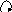
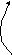
5 • D_R 1• 4 •

•3

3 • *

2 • * * •2 •5

1 • * * * •4

• • • • • 1 2 3 4 5 Е_R

Можно представить в виде схемы и матрицы:

• 5 5 •

•4 4 •

3 3

2 2

1 1

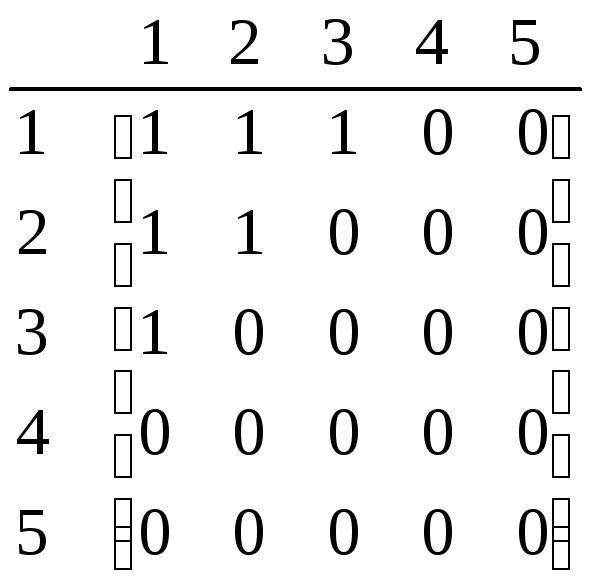
Отношение не рефлексивно, так как при условие не всегда выполняется. Отношение R на множестве Х не антирефлексивным согласно определению.

Отношение симметрично, так как , .

Пусть , т.е. и . Посмотрим, будет ли , т.е. . Преобразуем не всегда меньше 5, значит отношение не транзитивно.

Отношение R не является отношением эквивалентности.

Задание №6:

Дано множество и отношение . Показать, что отношение R является отношением порядка. Построить диаграмму Хассе частично упорядоченного множества существует ли во множестве Х наибольший и наименьший элемент? Существуют ли несравнимые элементы?

Решение:

Покажем, что отношение R рефлексивно, антисимметрично и транзитивно.

Рефлексивность имеет место, так как любое число является своим делителем, т.е. .

Пусть одновременно выполняются условия и , тогда .. Действительно, означает, что делитель , т.е. найдется целое число такое, что . Одновременно найдется целое число такое, что . Отсюда . Последнее равенство

выполняется при или , но все элементы множества - положительные числа, второй случай невозможен. Следовательно, , т.е. , и отношение R антисимметрично.

Пусть и , значит, найдутся такие, что , . Тогда где . Следовательно, х является делителем и . Отношение транзитивно.

Отношение R рефлексивно, антисимметрично, и транзитивно, т.е. является отношением порядка. Посмотрим диаграмму Хассе частично упорядоченного множества . На нижнем уровне диаграммы поместим элементы , не имеющие других делителей, кроме себя . На втором уровне – элементы, не имеющие других делителей, кроме себя и элементов нижнего уровня . Остальные элементы делятся сами на себя, на все элементы второго и первого уровней – помещаем его на третий уровень. Соединяем отрезком элементы соседних уровней, если элемент нижнего уровня является делителем элемента соседнего верхнего уровня. Диаграмма Хассе построена. Из диаграммы видно несравнимые элементы: 4 и 3, 3 и 2, 6 и 4 . Максимальные элементы 4 и 6, наименьший элемент 1.

4 6

2 3

1

Задание №7:

Заданы отношения:

R: S:

A1	A2	A3
a	b	c
a	c	d
b	d	a
d	a	b

B1	B2
a	d
a	c
c	d

Записать обозначения операций реляционной алгебры и выполнить их:

а) проекция отношения R список (1,3);

б) соединение отношений R и S по условию “A₂ = B₁” .

Решение:

C1	C2
a	c
a	d
b	a
d	b

D1 D2 D3 D4 D5

а с d c d d a b a d d a b a c

Задание №8:

Даны множества и Какова мощность множества ?

Решение:

Множество конечно и задано перечислением своих элементов, множество задано характеристическим свойством. Запишем несколько первых элементов множества, Видим, что и , т.е. множество - конечно.

Покажем, что счетное занумеруем его элементы:

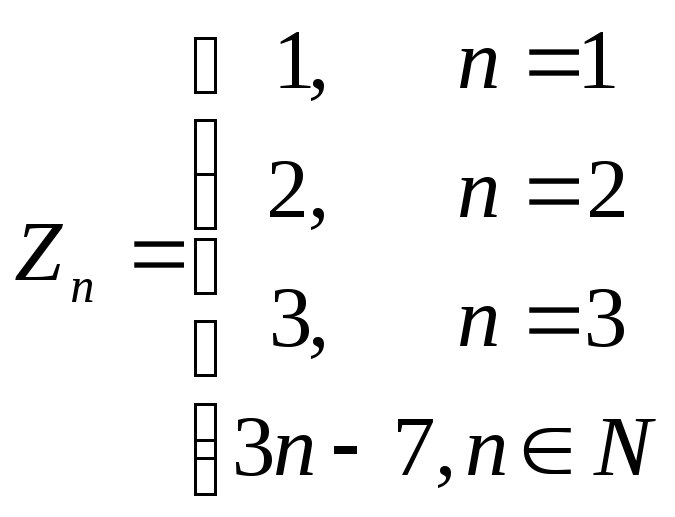
Задана биекция множества N на множество , следовательно, счетно и _0.