Сравнение бесконечно малых функций
Как было показано, сумма, разность и произведение БМФ являются БМФ. Это, вообще говоря, нельзя сказать о частном двух БМФ. Деление одной БМФ на дру- гую может привести к различным результатам.
Определение №6. БМФ
называется БМФ высшего порядка малости
по отношению к БМФ
если предел их отношения равен нулю при
Пример
№1.
Говорят, что БМФ имеет более высокий порядок малости, чем БМФ при
Определение №7.
БМФ
называется
БМФ низшего порядка малости по от-
ношению к БМФ
если предел их отношения равен
бесконечности при
Пример
№2.
Определение №8. Две
БМФ
и
называются БМФ одного порядка ма-лости,
если предел их отношения равен некоторому
конечному числу, отличному от
нуля:
.
Пример
№3.
БМФ одного порядка малости характеризуются как бы одинаковой скоростью стремления к нулю.
Определение №9. Две
БМФ
и
называются эквивалентными БМФ, если
предел их отношения равен единице:
Эквивалентные БМФ
и
обозначаются так:
Пример
№4.
Замечание №6. В некоторых случаях недостаточно знать, что одна из двух БМФ является БМФ более высокого порядка малости, чем другая. А нужно ещё оценить как высок этот порядок. Последнее имеет немаловажное значение при изучении характера изменения БМФ.
Определение №10.
БМФ
называется
БМФ k-го порядка малости по отно- шению
к БМФ
,
если
и
будут БМФ одного порядка малости:
.
Пример №5.
Здесь
и
называется БМФ 2-го порядка малости по
от- ношению к БМФ
Замечание №7. Существуют аналогичные правила сравнения для БМФ при
Определение №11.
Если
не существует, то
и
несравни- мые БМФ при
[7].
Теоремы об эквивалентности бмф
Теорема №3. Для
того, что БМФ
и
были эквивалентными необхо- димо и
достаточно, чтобы их разность
представляла собой БМФ более высокого
порядка малости, чем они сами, т.е.
Доказательство
Доказательство необходимости
1.
Пусть БМФ
эквивалентна БМФ
при
т.е.
Требуется доказать,
что
2.
Тогда
3.
Так как предел отношения двух БМФ
и
равен нулю, то БМФ
представляет собой БМФ высшего порядка
малости по отношению к БМФ
при
4. Аналогично,
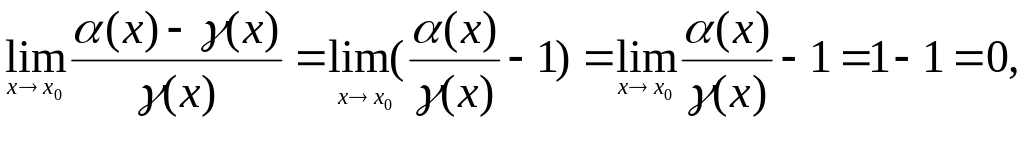
т.е.
БМФ
представляет собой БМФ высшего порядка
малости по отношению к БМФ
при
Доказательство достаточности
1. Пусть Требуется доказать, что при т.е.
2.
Преобразуем предел отношения
А
такое возможно тогда, когда
Ч.т.д.
Замечание №8. 1)
Из теоремы следует, что при замене
некоторой БМФ
эквивалентной ей БМФ
а)
допустимая абсолютная погрешность
б) допустимая
относительная погрешность
могут быть сделаны сколь угодно малыми.
2) Поэтому часто при различных действиях над бесконечно малой прибегают к приближённой замене одних БМФ им эквивалентными, имеющими более простой вид [8].
Теорема №4. Пусть
даны две пары БМФ
и
Причём,
эквивалентна
а
эквивалентна
Тогда
в предположении, что хотя бы один из
этих пределов существует.
Доказательство
1.
Пусть
Требуется доказать,
что
если хотя бы один из этих преде- лов
существует.
2.
Рассмотрим отношение
4.
Получим:
5.
Перейдя к пределу в равенстве п.4 и
используя теорему о пределе произведения,
получим:
6.
Так как по условию теоремы
то получим
Ч.т.д.
Замечание №9. Эта
теорема может быть использована при
раскрытии неоп- ределённости вида
Замечание №10. Из теоремы следует, что при нахождении предела отноше- ния двух БМФ каждую из них можно заменить любой эквивалентной БМФ и от этого предел не изменится. При удачно выбранной замене задача раскрытия не- определённостей может быть значительно упрощена [3].