Анатомия математических моделей (переменные состояния, внешние переменные, контролирующие переменные, математические уравнения, параметры, универсальные константы)
Переменные состояния модели - Элементы множества (X) – являются индикаторами состояния системы (для почв и экосистем это могут быть, например, запасы и концентрации вещества, численность организмов).
Внешние переменные модели - характеристики внешних систем, образующих множество (Е), представляющее окружающую среду. Например, климатические характеристики.
Контролирующие переменные - Те из внешних переменных, которые человек может контролировать и таким образом управлять системой, например, доза удобрений, норма полива и др.
Математические уравнения- отношения между переменными состояния и внешними переменными.
Параметры моделей - коэффициенты уравнений.
Универсальные константы. Универсальные константы, такие, как газовая постоянная или атомный вес используются во многих моделях.
Вычислительный эксперимент и его достоинства.
Вычислительным экспериментом называется методология научных исследований, основанная на математическом моделировании и компьютерных технологиях. Мощность современных компьютеров позволяет проводить предварительные вычислительные эксперименты, способствующие эффективному осуществлению серьезных крупномасштабных экологических проектов.
Проведение вычислительного эксперимента можно условно разбить на три этапа: модель‐алгоритм‐программа (Самарский, Михайлов, 2001).
На первом этапе строится или подбирается модель, которая в математической форме описывает основные свойства изучаемой системы в соответствии с поставленными задачами. На этом этапе модель исследуется аналитически, что позволяет получить предварительные знания о качественном поведении системы.
Второй этап – выбор или разработка алгоритма для реализации модели на компьютере. Модель представляется в форме удобной для применения численных методов, определяется последовательность вычислительных и логических операций, которые нужно произвести, чтобы найти искомые величины с заданной точностью. Вычислительные алгоритмы не должны искажать основные свойства модели и быть экономичными.
Третий этап – создание программы, переводящей модель и алгоритм на доступный компьютеру язык. Затем триада «модель‐алгоритм‐программа» отлаживается и тестируется. При этом возможно возвращение на предыдущие этапы для внесения необходимых поправок. После того, как достаточное соответствие (адекватность) триады изучаемой системе установлены, она превращается в гибкий инструмент исследования, позволяющий проводить вычислительные эксперименты по изучению свойств и поведения изучаемой системы.
Вычислительный эксперимент возможен там, где нельзя провести натурный эксперимент, например, из‐за слишком большой продолжительности, опасности, дороговизны, риска разрушить изучаемую систему. Вычислительный эксперимент позволяет относительно быстро и дешево исследовать свойства и поведение изучаемой системы в любых мыслимых ситуациях. Важно отметить, что вычислительный эксперимент приводит к успеху при выполнении определенных условий: четкой формулировки целей и задач исследования; адекватности используемых моделей; достаточного количества надежных экспериментальных данных для определения параметров модели и необходимой точности вычислительных алгоритмов.
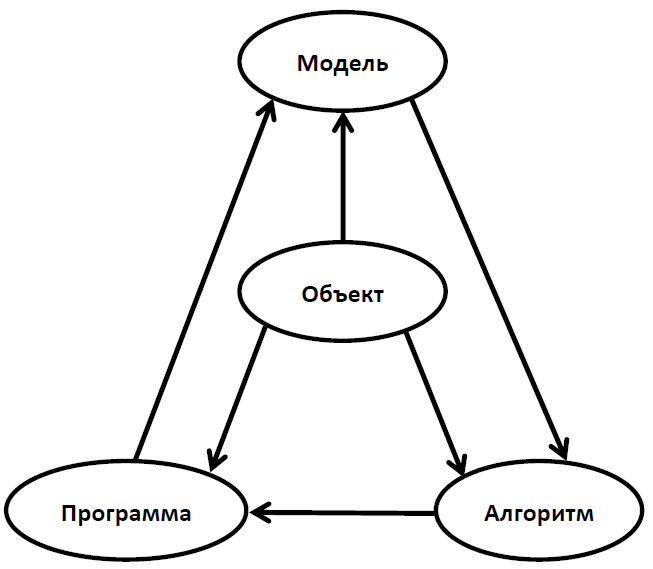
Схема вычислительного эксперимента (по Самарскому и Михайлову, 2001).
Классификации математических моделей (исследовательские-прикладные; аналитические-алгоритмические; минимальные - имитационные; линейные - нелинейные; статические -динамические; точечные- пространственно-распределенные; детерминированные стохастические)
Широкое распространение моделирования и многообразие моделей потребовало их упорядочивания. В связи с этим было предложено множество классификаций моделей, в основе которых лежат различные признаки их разделения. Модели классифицируют по целям моделирования, способам реализации, используемому математическому аппарату и другим характеристикам. В качестве примера приведем наиболее известные в экологии и почвоведении классификации моделей. На рисунке ниже представлена схематическая классификация моделей, предложенная В.Д. Федоровым и Т.Г. Гильмановым (1980).
Она построена в форме дихотомий. По способу реализации модели разделяются на реальные и идеальные. Примером реальной модели может служить почвенная колонка. Проблемы использования реальных моделей связаны с определением степени их адекватности изучаемой системе и с техническими трудностями. Гораздо больше возможностей представляют идеальные модели, так как они не ограничены возможностями физической реализации. Идеальные модели бывают концептуальными и математическими. Концептуальная модель это концептуальная структура (система взглядов), в рамках которой мы анализируем факты.
Концептуальные модели выражают в словесной (вербальные) и (или) графической (например, в виде диаграмм) форме. Настоящий курс посвящен обсуждению только математических моделей. Математические модели подразделяются на два класса аналитические и алгоритмические (численные, имитационные).
Аналитические модели – результаты представлены в виде аналитических выражений (формул), отражающих функциональные зависимости результатов (выходов) от внешних переменных и внутренних характеристик моделируемого объекта. Аналитические модели представляют особый интерес, так как с меньшими вычислительными затратами позволяют изучать фундаментальные свойства изучаемого объекта, его качественное поведение (возможно без ЭВМ). К сожалению, аналитическое решение можно получить только для относительно простых моделей. В большинстве случаев приходится использовать алгоритмические подходы, позволяющие получить лишь приближенное численное решение.
Численные (алгоритмические) модели – результаты представлены в численном виде путем реализации алгоритма решения в виде компьютерной программы.
К классу алгоритмических моделей относятся имитационные (портретные) модели. В настоящее время эти модели широко используются при изучении сложных динамических систем. При построении имитационной модели, как правило, стараются максимально использовать имеющуюся информацию об изучаемой системе и в соответствии с задачами исследования представить все основные взаимодействия между ее компонентами в сочетании с внешними воздействиями. Это модели высокой степени подробности с большим числом переменных и параметров. Проведение вычислительных экспериментов на основе имитационной модели позволяет проигрывать различные сценарии поведения системы.
Аналитические и алгоритмические модели относятся к классу статических или динамических в зависимости от того описывают ли они поведение моделируемого объекта во времени. В статических моделях нет временного параметра. Среди параметров динамических моделей всегда есть временной параметр, они демонстрируют динамику поведения объекта.
По характеру описания динамики моделируемого объекта различают дискретные и непрерывные модели. В дискретных моделях значения переменных состояния определяются только для фиксированных моментов времени, а в непрерывных для всех моментов из рассматриваемого временного интервала.
По степени определенности предсказания модели подразделяют на детерминированные и стохастические (вероятностные).
В детерминированных моделях значения выходных переменных определяются однозначно с точностью до ошибок вычислений. В стохастических моделях определяются распределения вероятности возможных значений выходных переменных, характеризуемые такими показателями, как математическое ожидание, дисперсия и др.
По виду используемых функций модели бывают линейными и нелинейными.
В зависимости от того описывают ли модели изменения переменных состояния в пространстве, они относятся к классу пространственно – распределенных или точечных (локальных). Например, в точечных моделях динамики азота в почве в качестве переменных состояния можно взять усредненные по площади значения концентраций различных форм азота в гумусовом горизонте. В пространственно‐распределенных моделях переменные состояния зависят не только от времени, но от пространственных координат. Пространственно‐распределенные модели динамики азота в почве будут описывать изменения содержания различных форм азота не только во времени, но и с глубиной по профилю почвы, а в более сложном варианте по всем трем пространственным координатам.
Г.Ю. Ризниченко (2002) в соответствии с целями моделирования подразделяет математические модели в биологии на три больших класса: регрессионные, имитационные и качественные (базовые).
Первый класс – регрессионные модели, которые представляют результаты статистического анализа данных, полученных путем наблюдений или экспериментов, в виде эмпирических формул. Они не описывают механизмов изучаемых процессов и не раскрывают причинно‐следственные связи, что исключает возможность использования регрессионных моделей для условий, отличающихся от тех, при которых получены экспериментальные данные.
Второй класс – имитационные модели конкретных биосистем, максимально учитывающие имеющуюся информацию об объекте. Как правило, они построены по модульному принципу. Причем каждый модуль верифицируется до его включения в общую модель. Имитационные модели применяются для описания объектов различного уровня организации живой материи – от биомакромолекул до моделей биогеоценозов. Они легки для понимания, интерпретации и развития. После предварительной калибровки имитационная модель, построенная для одной системы, может применяться для других систем подобного типа. Недостатком этого класса моделей является большая информационная емкость и трудности калибровки из‐за большого числа параметров.
Третий класс – качественные (базовые) модели. Они представляют основную «минимальную» структуру изучаемых систем. Поэтому для этого класса моделей Н.Н. Моисеевым и Ю.М. Свирежевым (1979) было предложено название «минимальные модели». Базовые модели направлены на описание основных динамических свойств изучаемых систем. Качественное исследование базовых моделей позволяет понять суть явлений, происходящих в сложных системах. Заметим, что математическая формализация минимальной структуры, очевидно, не единственна, и поэтому для одной системы может быть построено несколько минимальных моделей. Почвы и биогеоценозы являются открытыми для потоков вещества и энергии нелинейными системами. Поэтому базовые (минимальные) модели математической экологии представлены нелинейными моделями. Эти достаточно простые, не отягощенные деталями модели позволяют изучать такие общие свойства почв и экосистем как множественность стационарных состояний, возможность перехода из одного состояния в другое, пространственная неоднородность и квазистохастичность. Примером минимальной модели в экологии может служить классическая модель экосистемы «хищник‐жертва», предложенная Вольтерра, который заложил фундаментальные основы теории биологических сообществ, построенной именно как математическая теория. В почвоведении в качестве примеров минимальных моделей можно назвать модель «идеального» подзола (Морозов, 2007) и нелинейные модели динамики органического вещества почв (Смагин и др., 2001; Рыжова, 2003).
Несмотря на развитие вычислительной техники, которая уже сегодня позволяет строить и исследовать сложные имитационные модели почв и экосистем, со временем интерес к базовым моделям будет только возрастать.
Йоргенсен (Jørgensen, 2008) в широком спектре современных экологических моделей выделил следующие одиннадцать типов.