I. Теоретические сведения.

1. Метод последовательных подстановок.

Решение системы сравнений первой степени с одним неизвестным

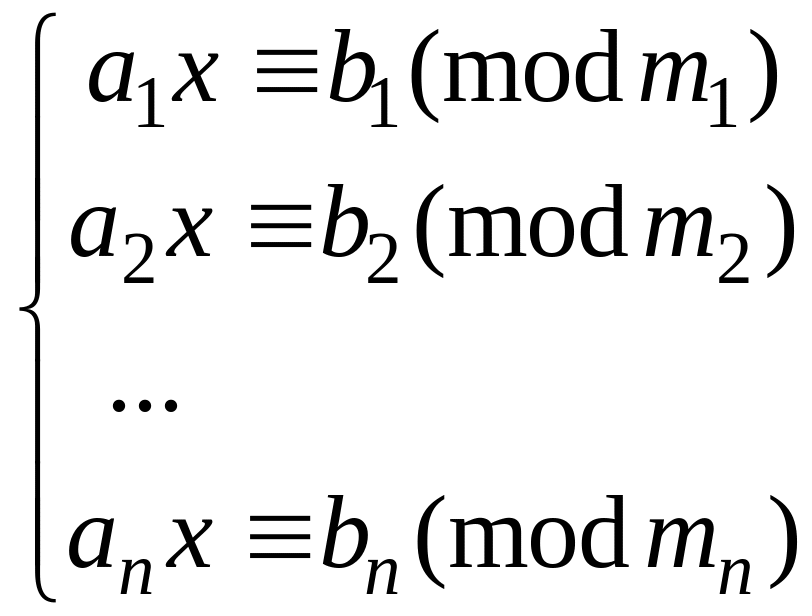(5)

можно получить следующим образом. Сначала решаются сравнения по отдельности (любым из известных методов). Может оказаться (если , и не делится на ), что какое-либо сравнение системы (5) не имеет решений; тогда нет решений и у системы. Возможно, какие-либо сравнения имеют несколько решений (если , и делится на ). Беря по одному решению для каждого сравнения, получаем систему

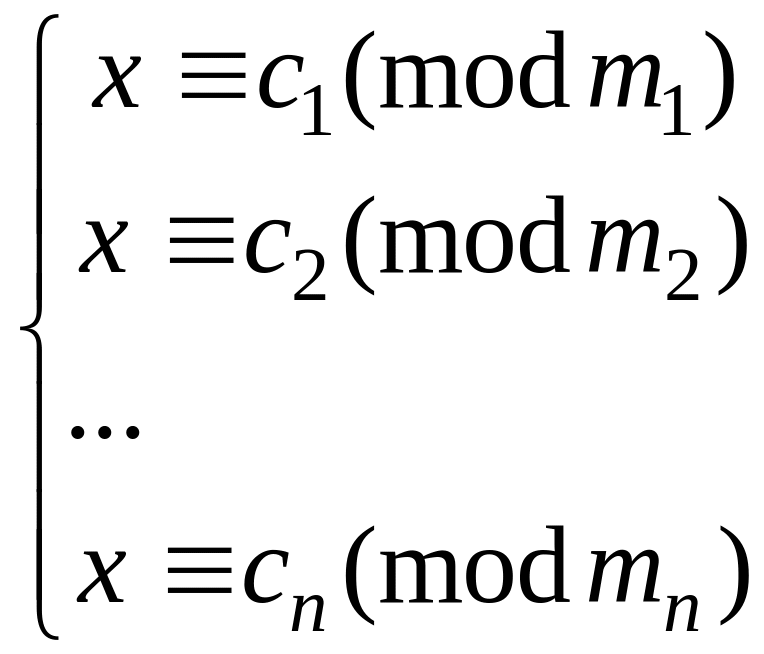. (6)

Затем решение первого сравнения системы (6) представляется в виде

.

Подставляя это выражение во второе сравнение системы (6), находим, при каких значениях удовлетворяются первые два сравнения системы. Тогда

.

Подставляя полученное выражение для в третье сравнение системы (6), находим выражение для . Так продолжаем вплоть до подстановки в последнее сравнение.

2. Китайский алгоритм.

В ситуации, когда у системы (6) модули попарно взаимно просты, справедлива китайская теорема об остатках:

Пусть натуральные числа попарно взаимно просты. Тогда:

1. Для любых целых чисел таких, что , найдётся число , которое при делении на даёт остаток .

2. Если числа и обладают указанным свойством, то .

Таким образом, по модулю система (6) имеет единственное решение. Это решение может быть найдено с помощью «китайского алгоритма»:

а. Вычисляются

,

,

…

.

б. Решением сравнений первой степени находятся числа , для которых .

Вычисляется решение системы в виде

II. Примеры.

1. Метод последовательных подстановок.

Решим систему сравнений:

.

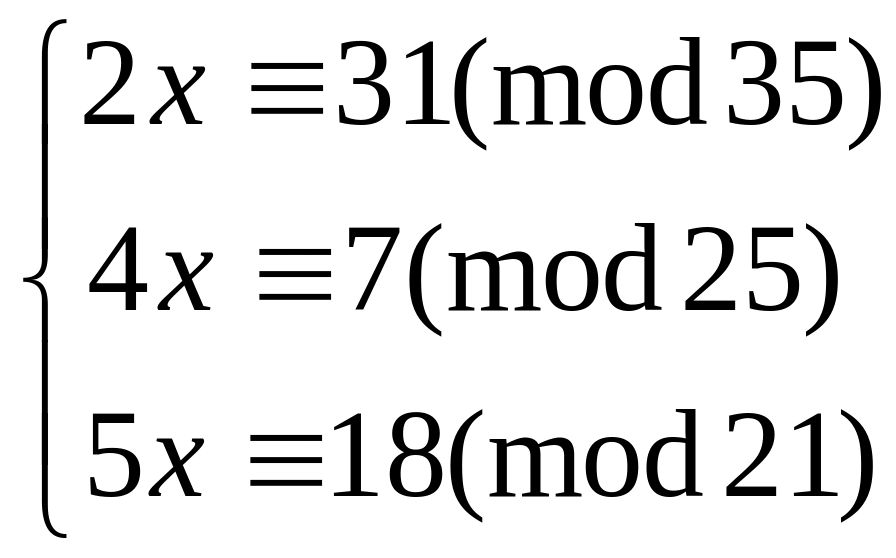Поскольку , то каждое отдельное сравнение имеет решением единственный класс вычетов:

.

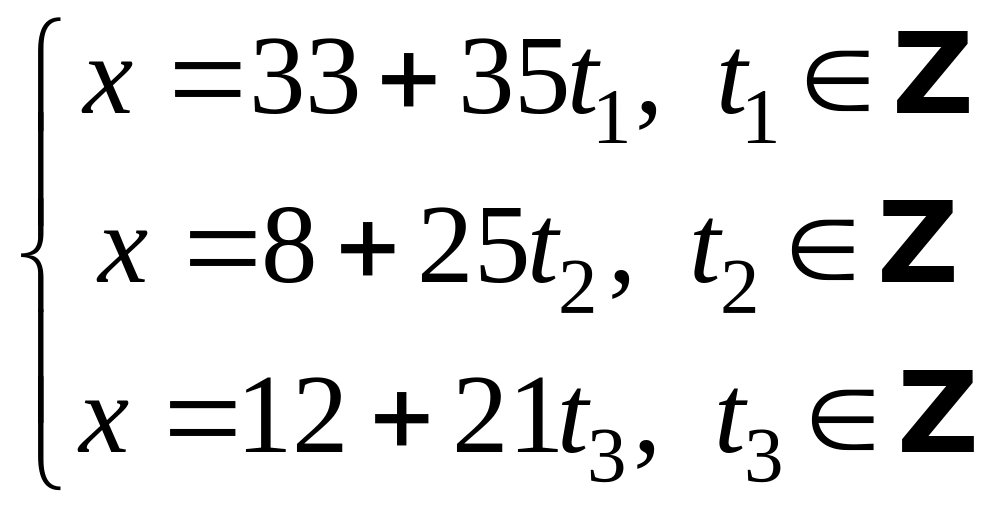Подставляем во второе сравнение и решаем его относительно :

.

Здесь , и свободный член сравнения также делится на . Деля все члены сравнения на , получаем . Таким образом, одно из решений . Тогда

.

Остаётся выяснить, при каких значениях это выражение удовлетворяет третьему сравнению:

.

Все члены сравнения делятся на . Приходим к сравнению . Тогда

.

Проверка показывает, что эти значения удовлетворяют каждому сравнению исходной системы. Заметим, что НОК( .

2. Китайский алгоритм.

Решим систему сравнений:

.

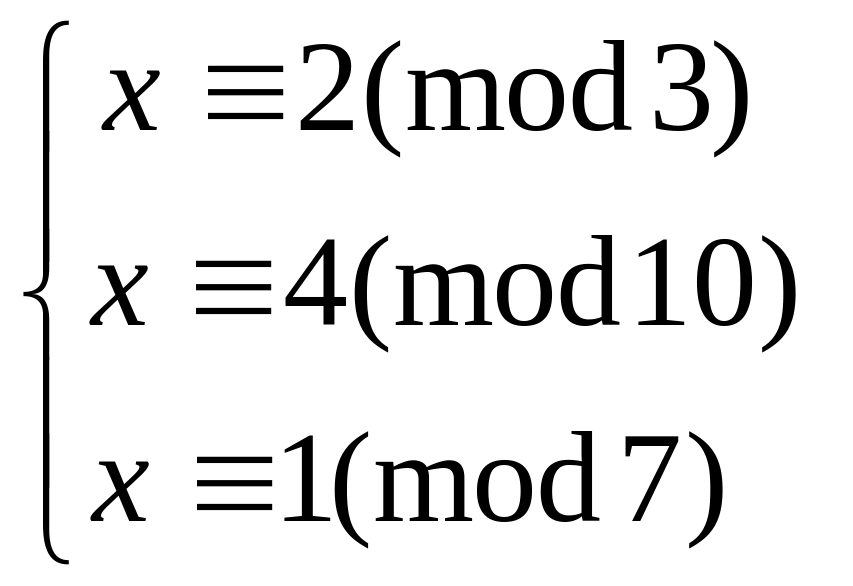Модули попарно взаимно просты. . Далее,

;   ; .

Решаем сравнения:

;

;

.

Окончательно

,

или

.

III. Задания.

№ вар.	Решить систему методом подстановки	Решить систему китайским алгоритмом
1
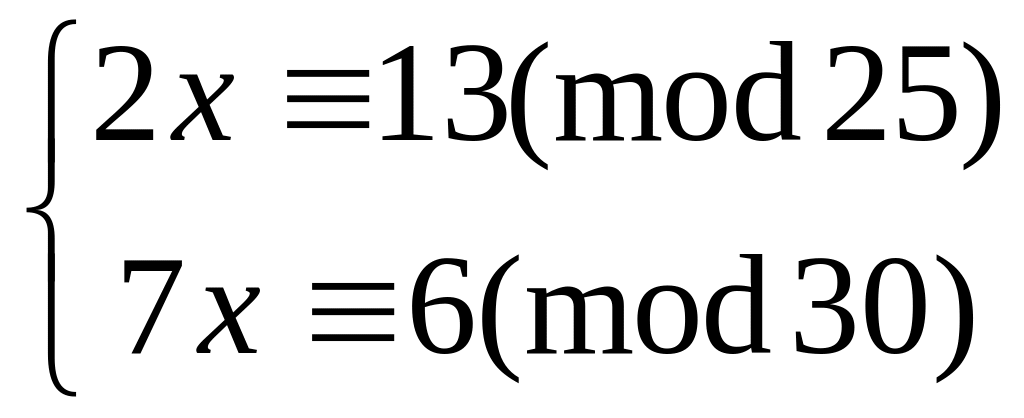
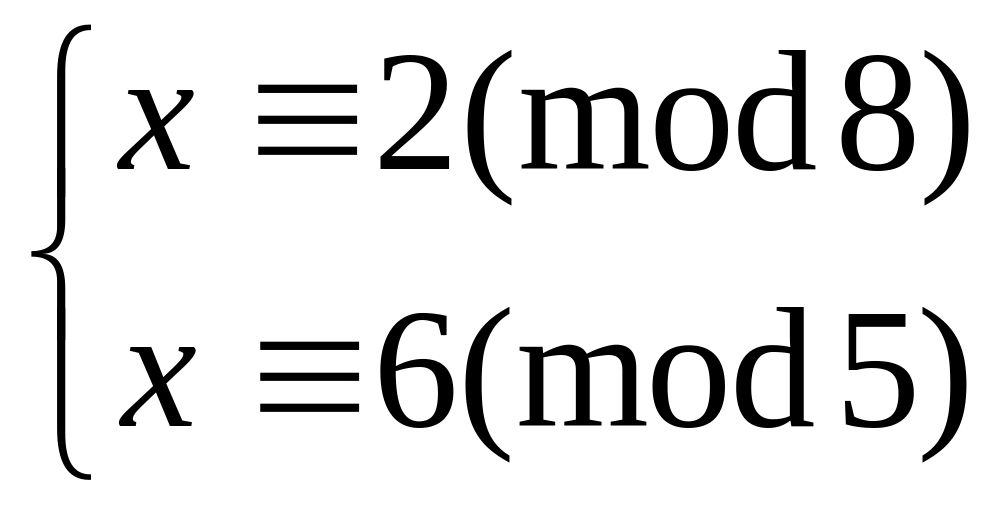
2
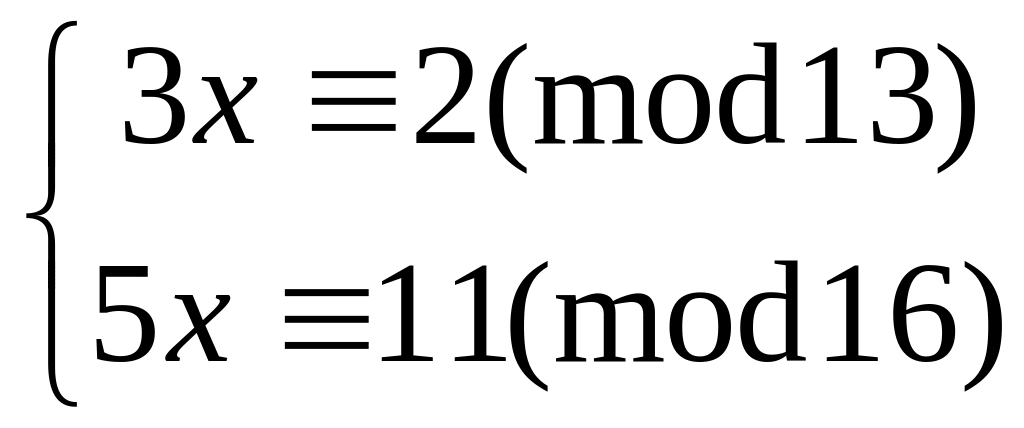
3
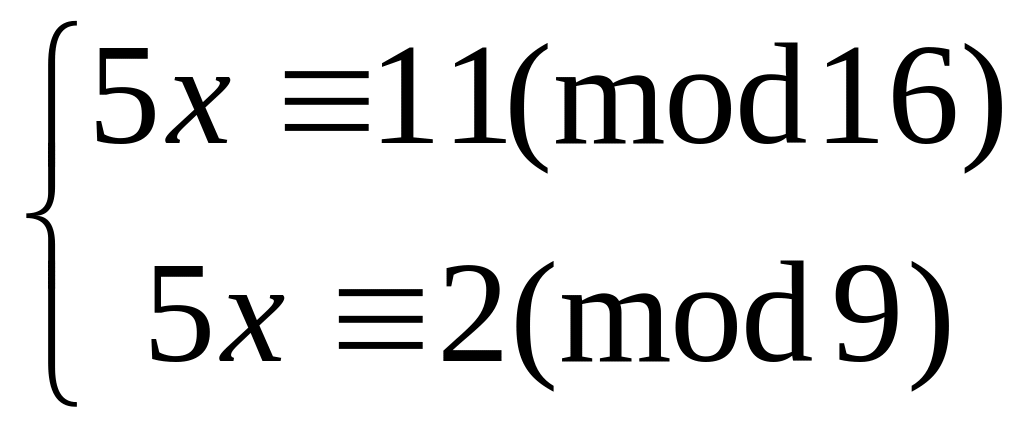
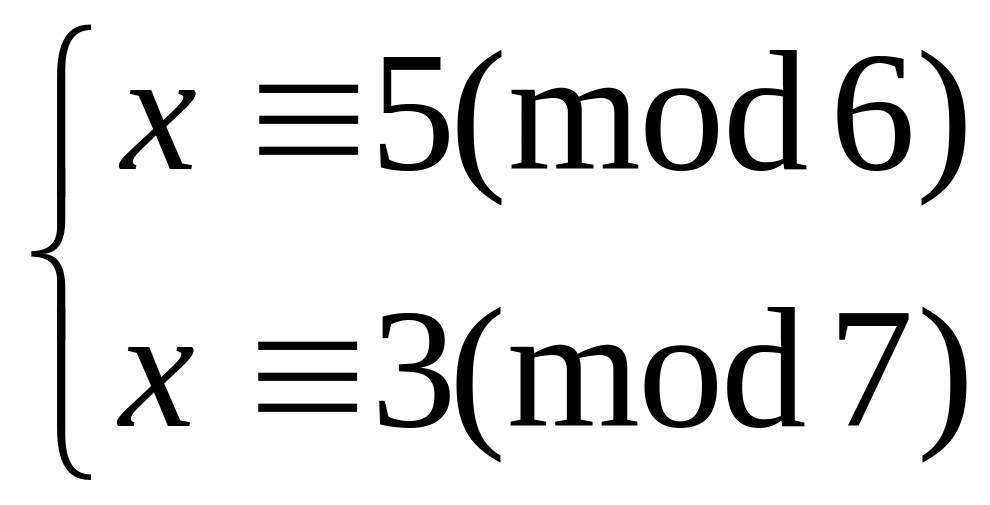
4
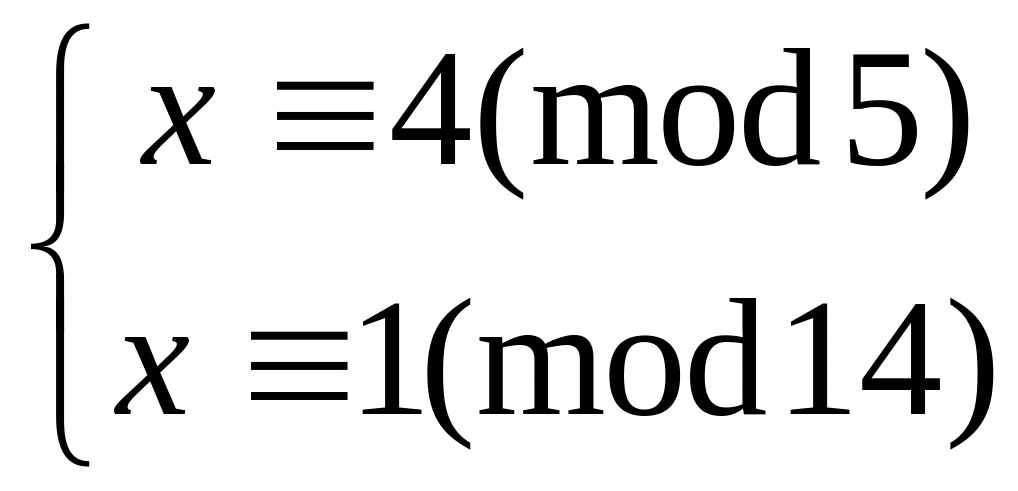
5
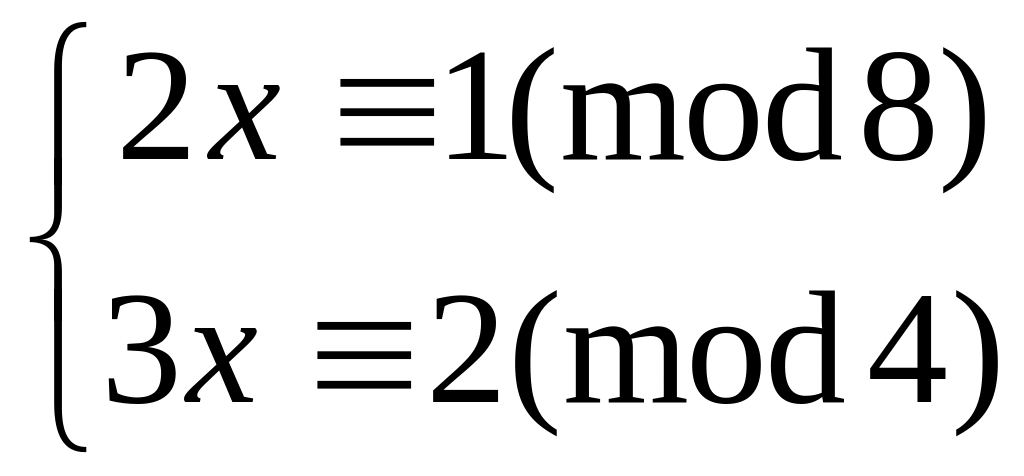
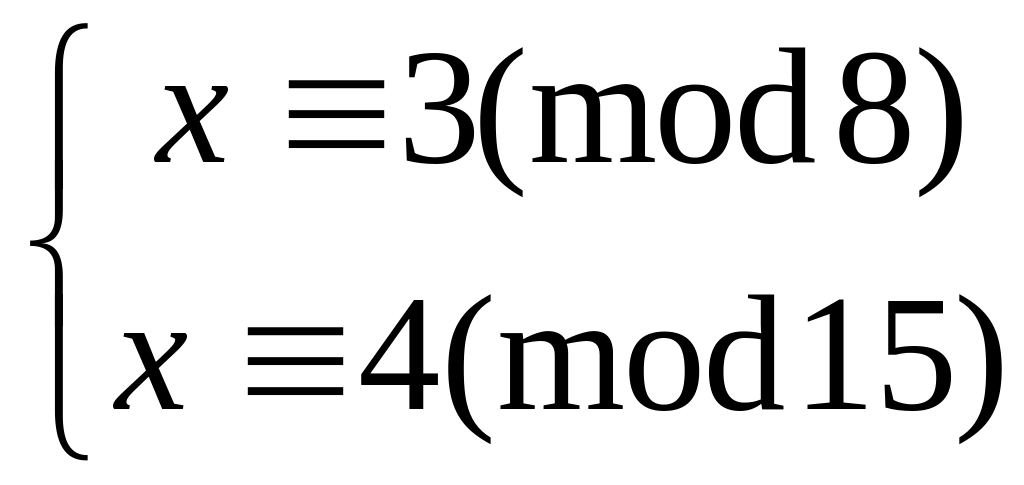
6
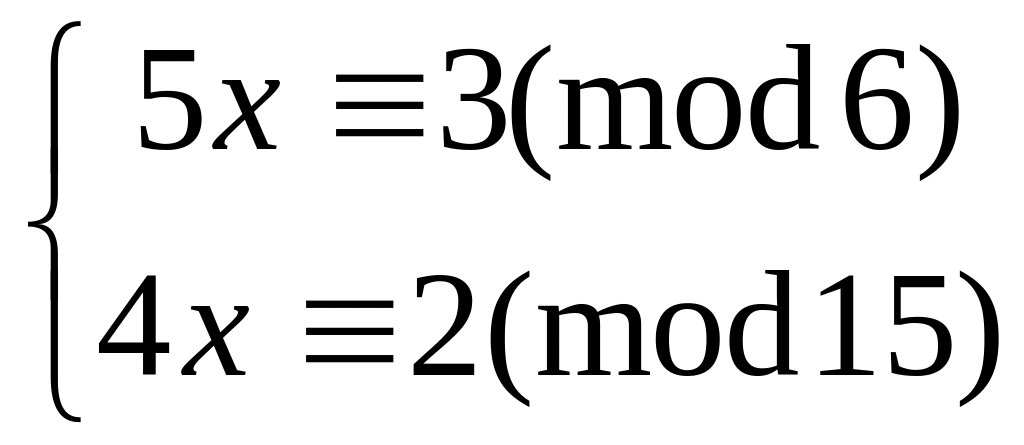
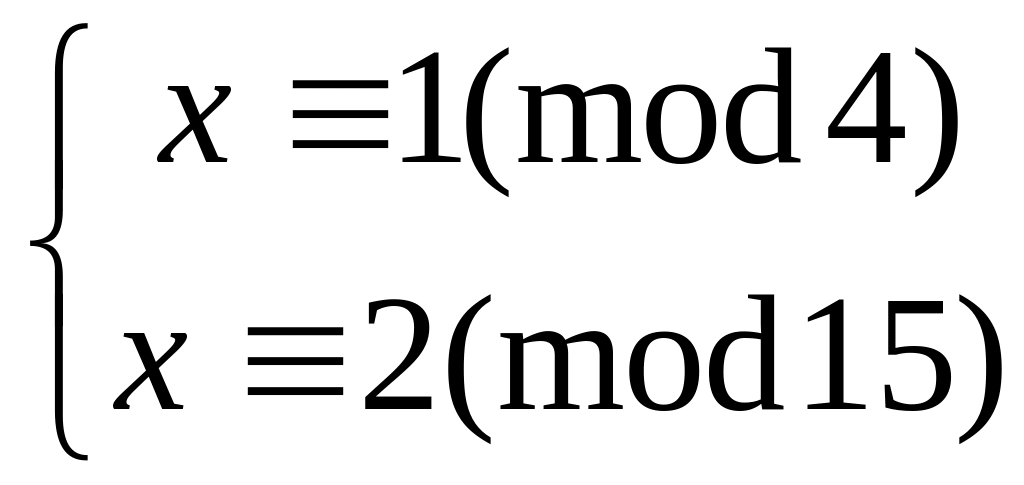
7
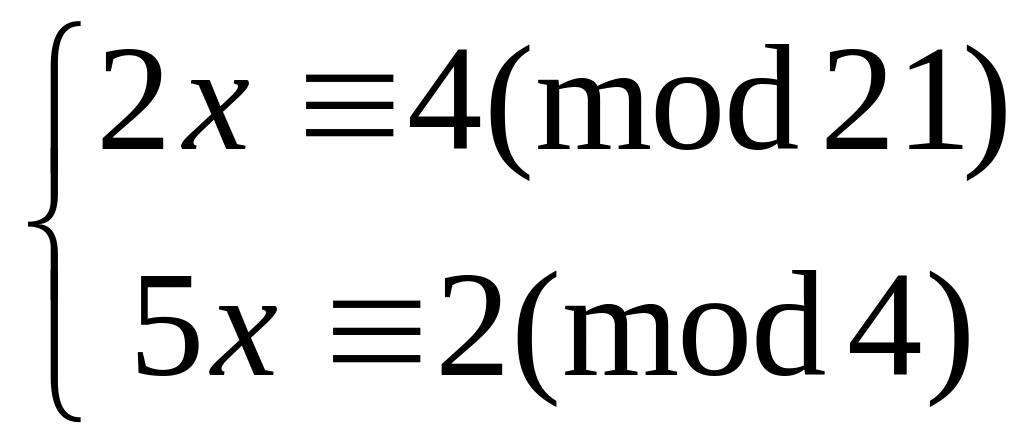
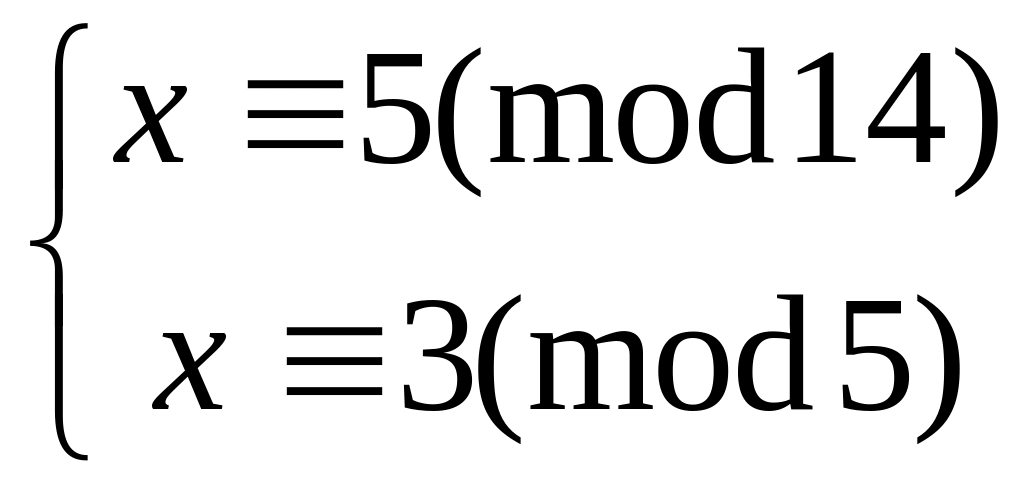
8
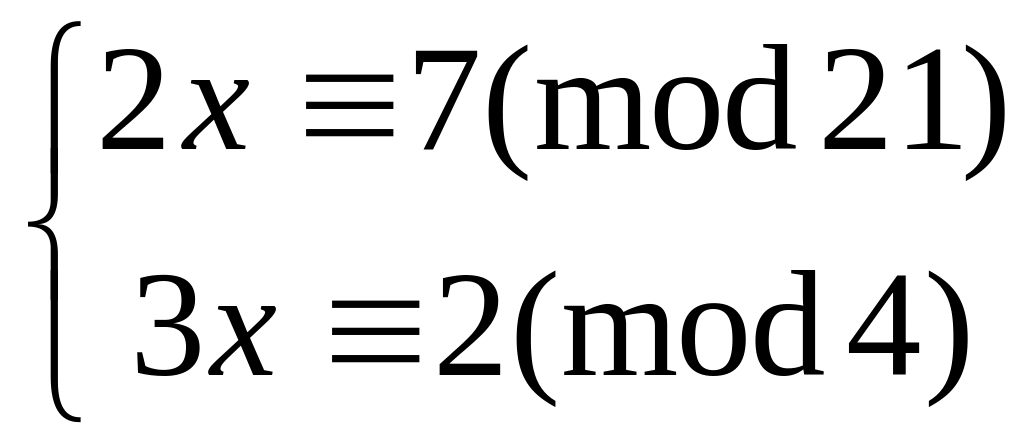
9
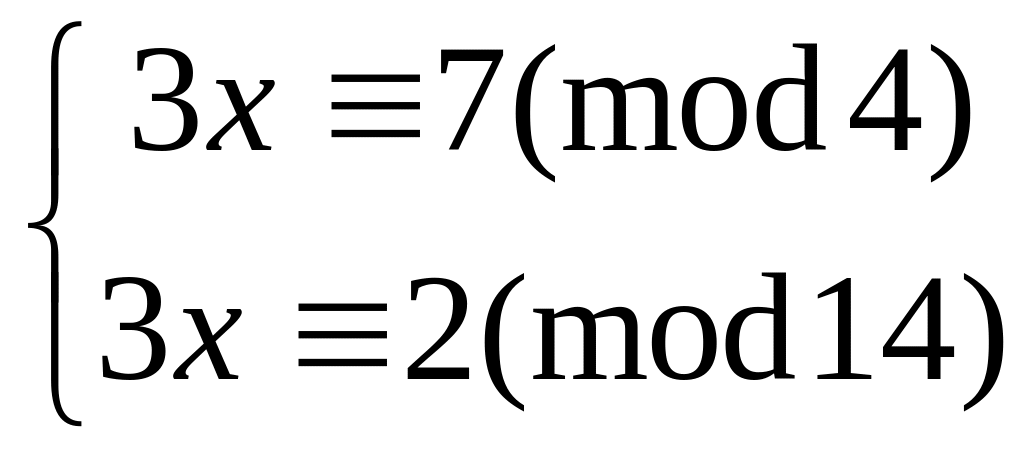
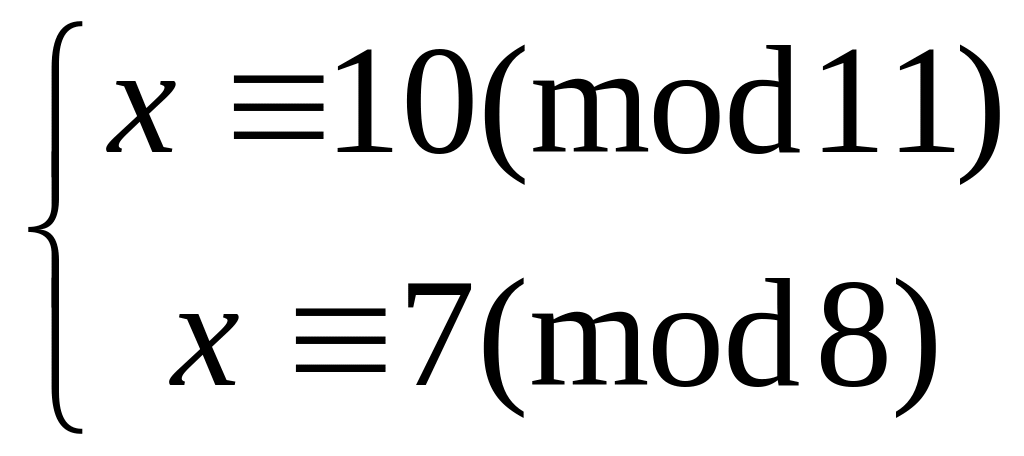
10
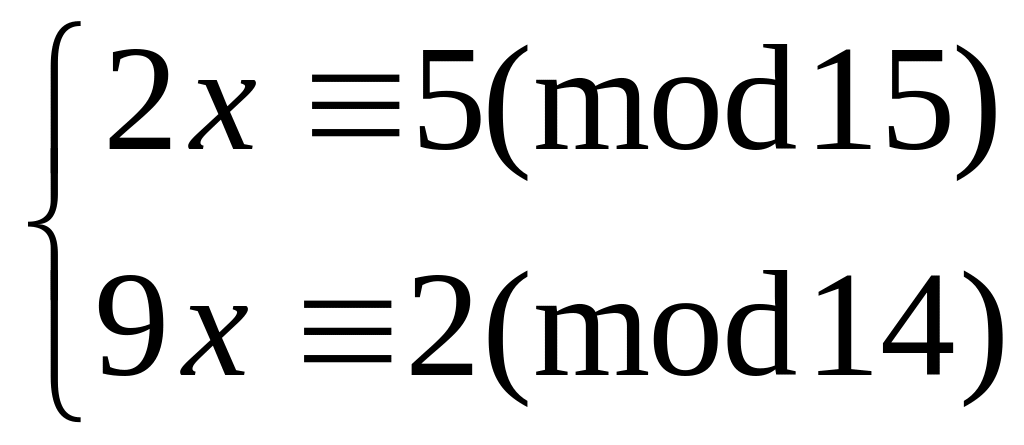
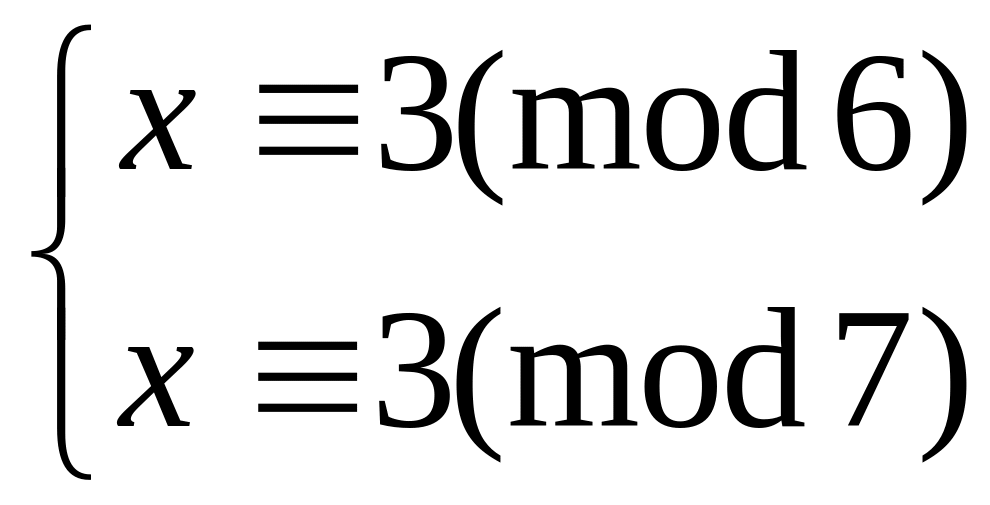
11
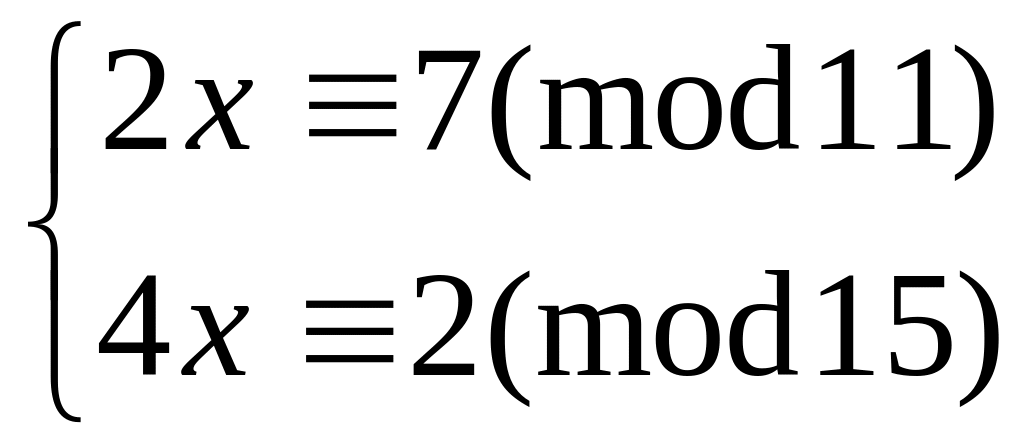
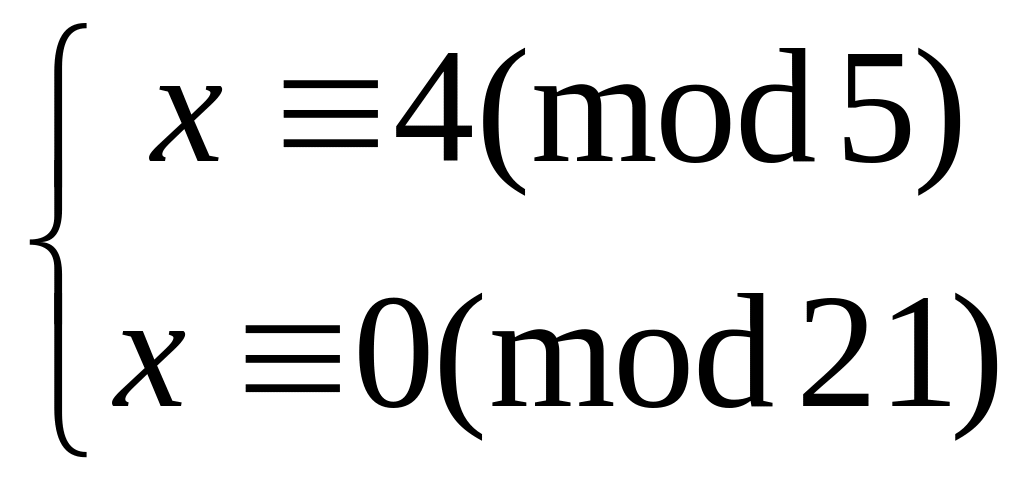
12
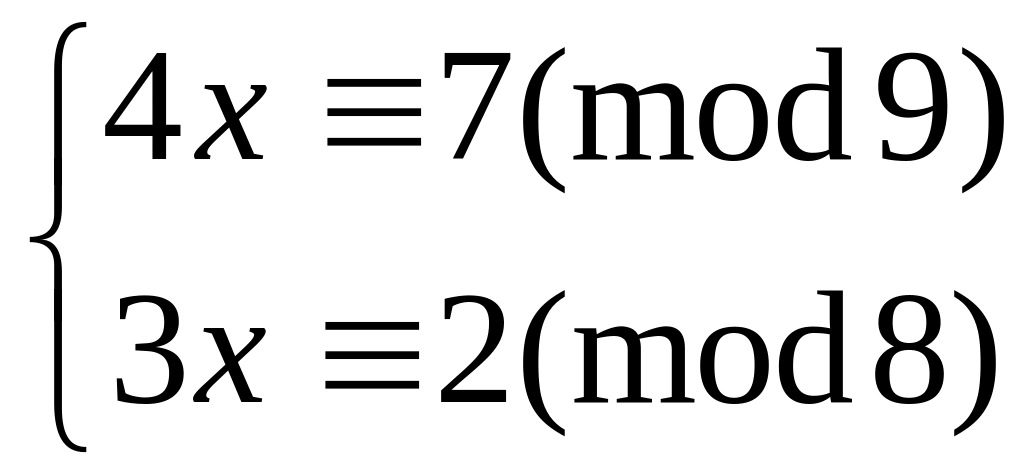
13
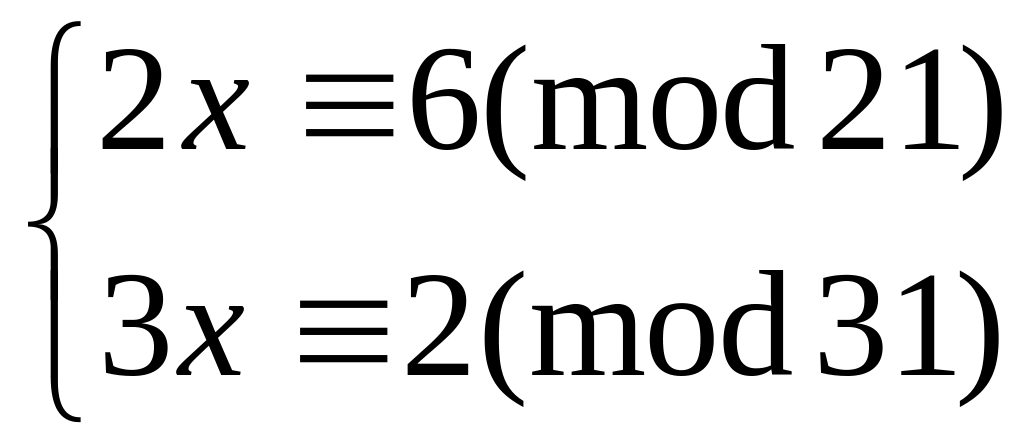
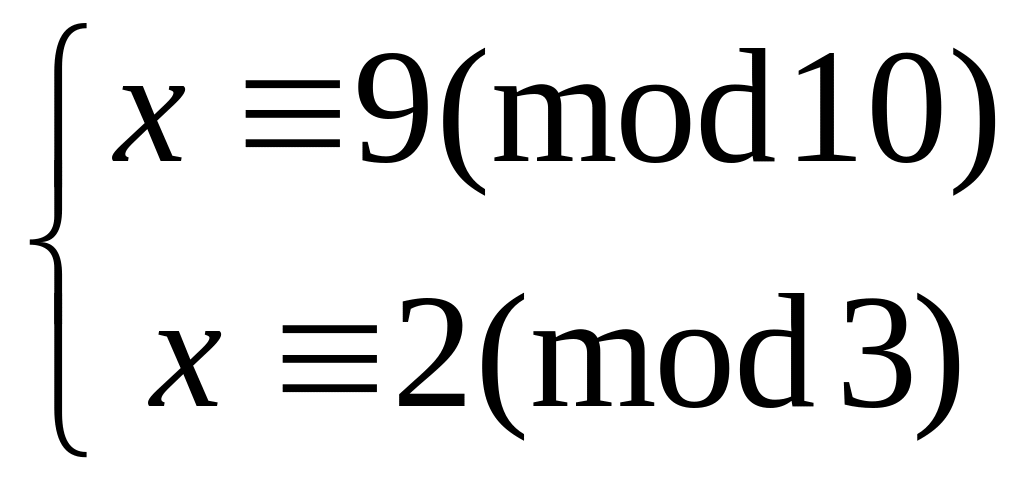
14
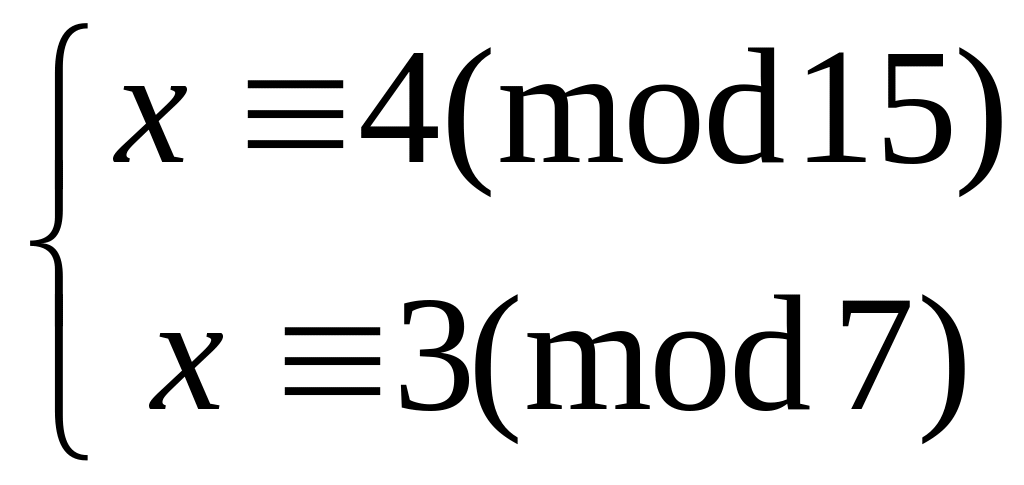
15
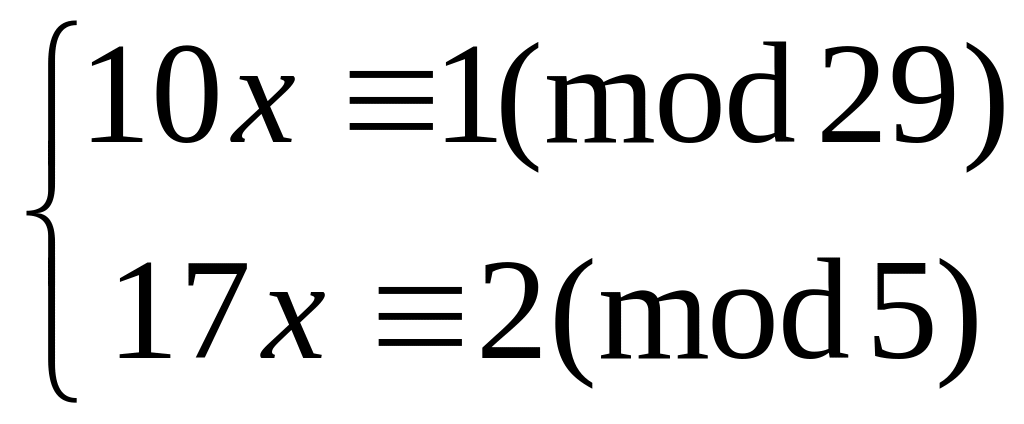
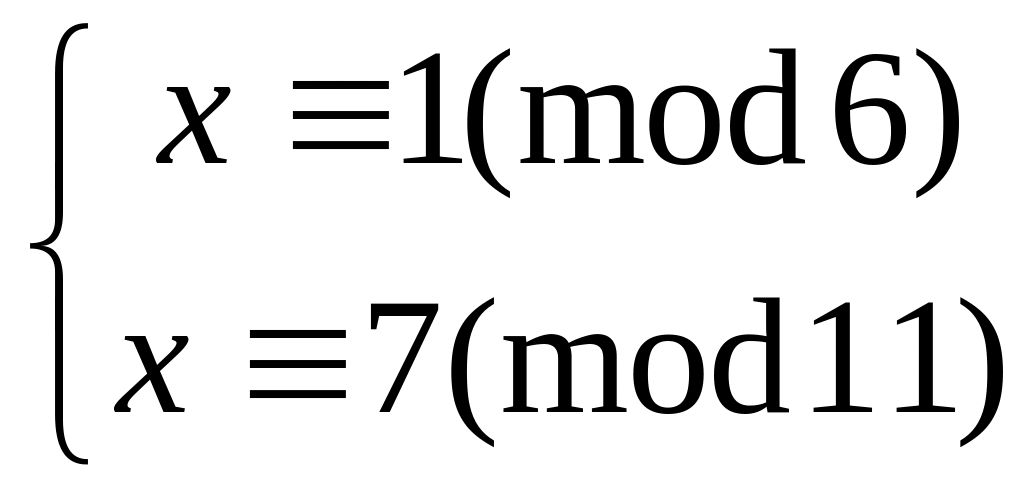
16
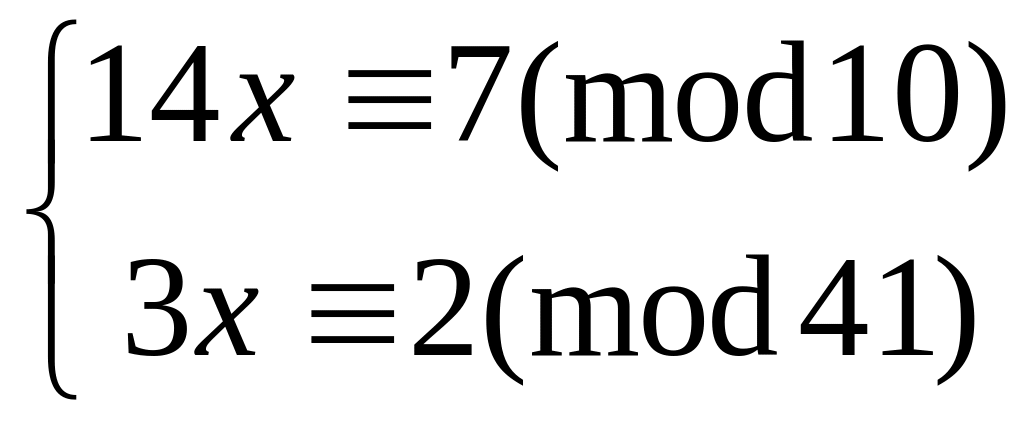
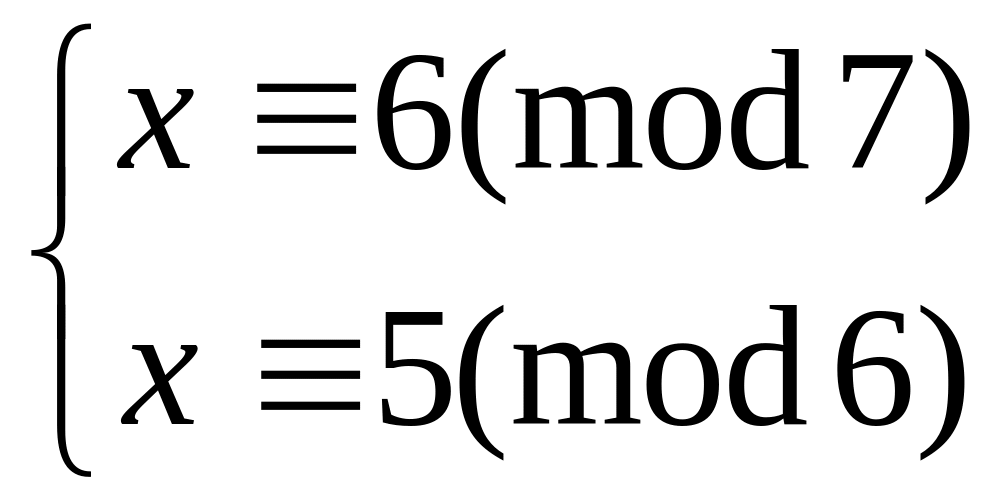
17
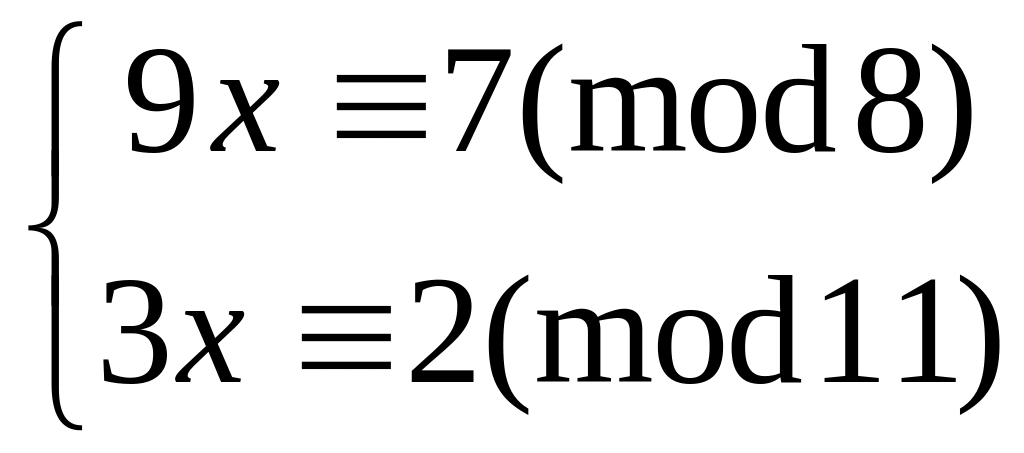
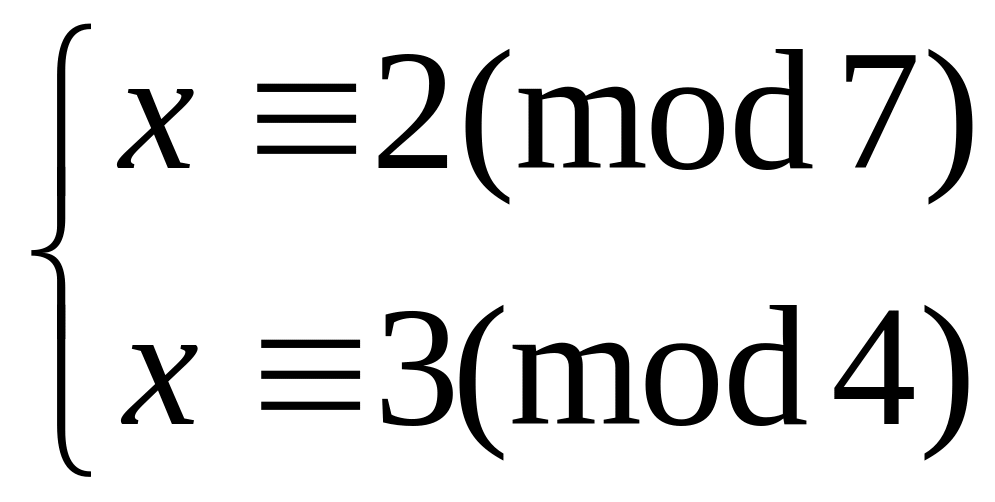
18
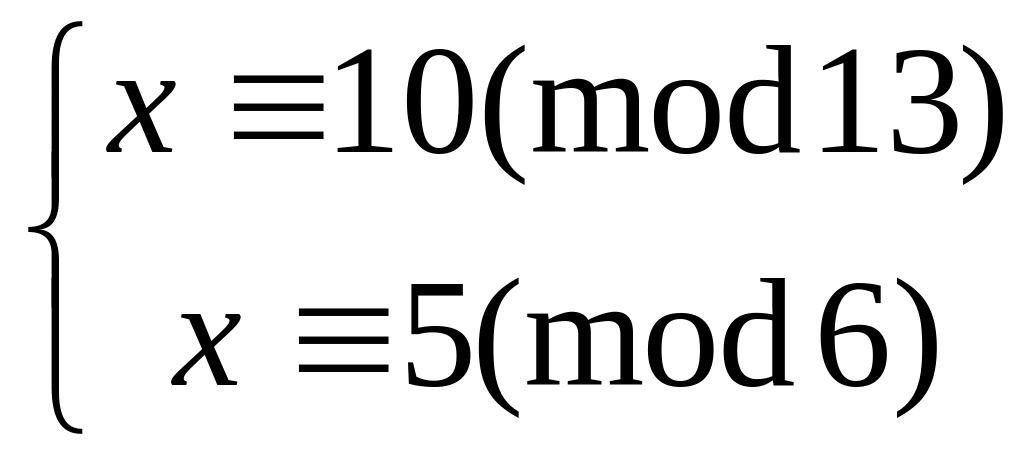
19
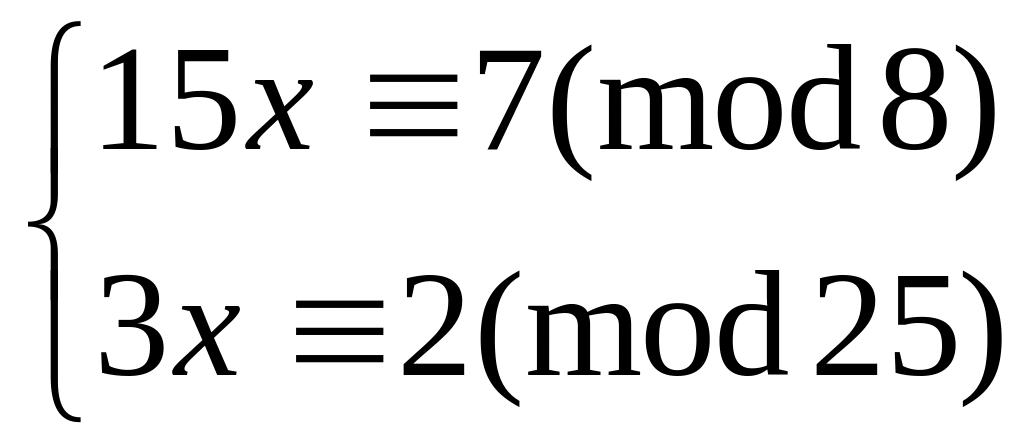
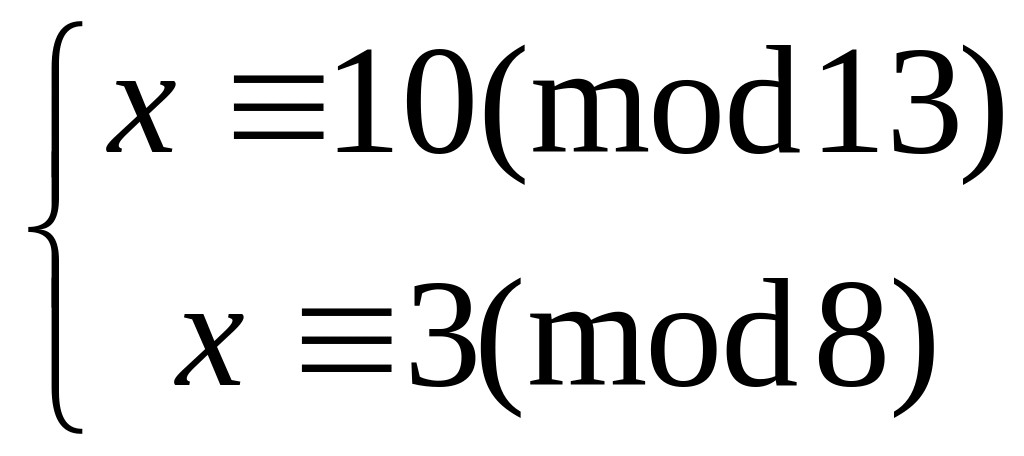
20
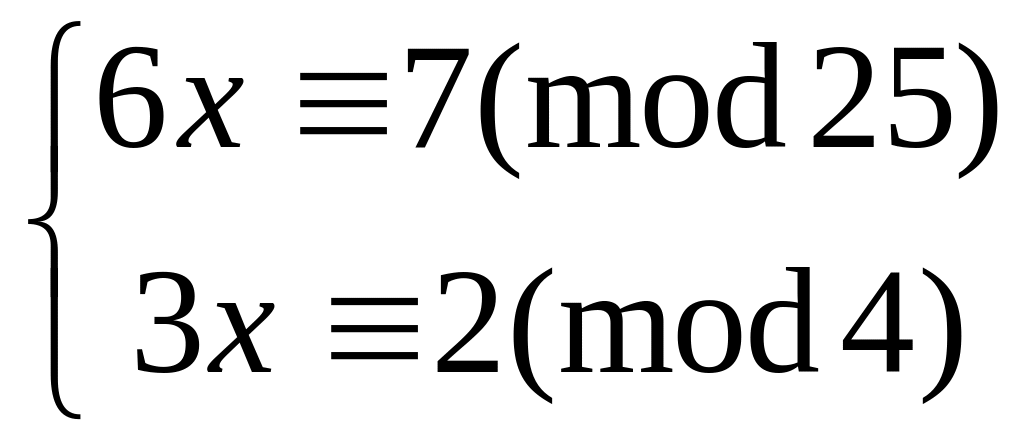
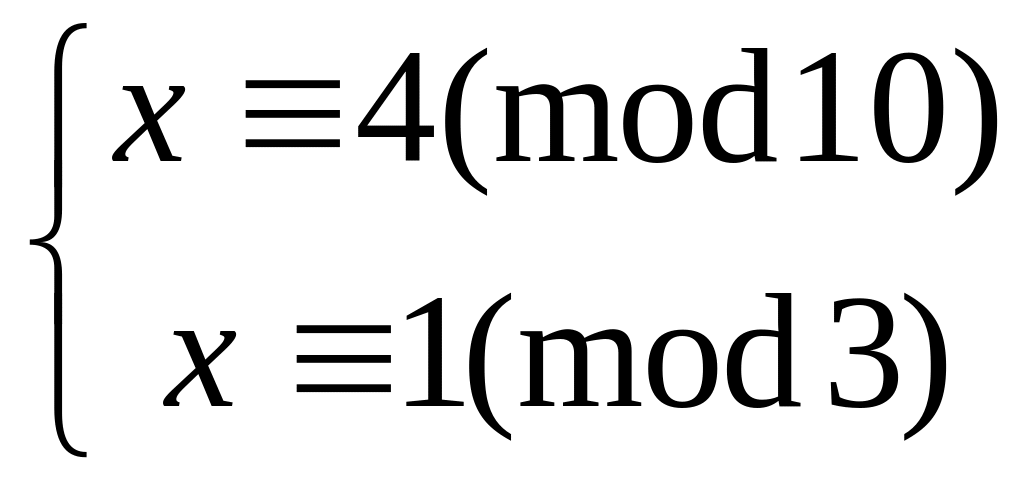
21
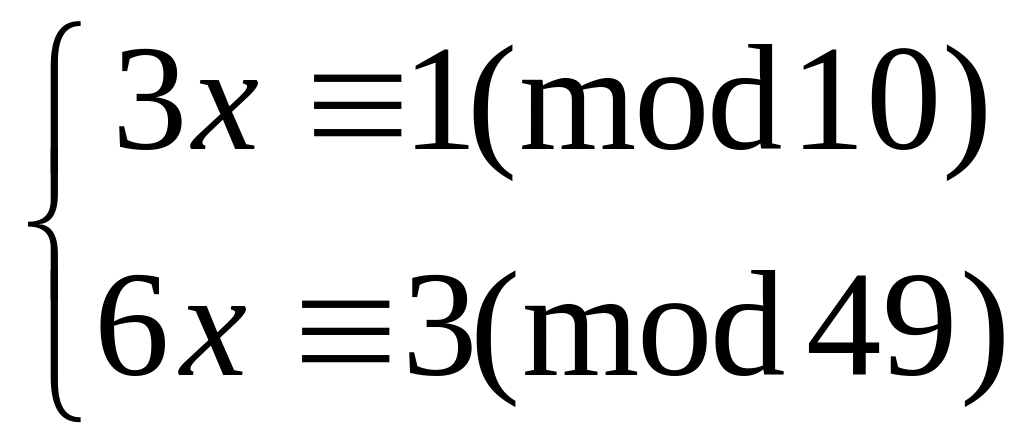
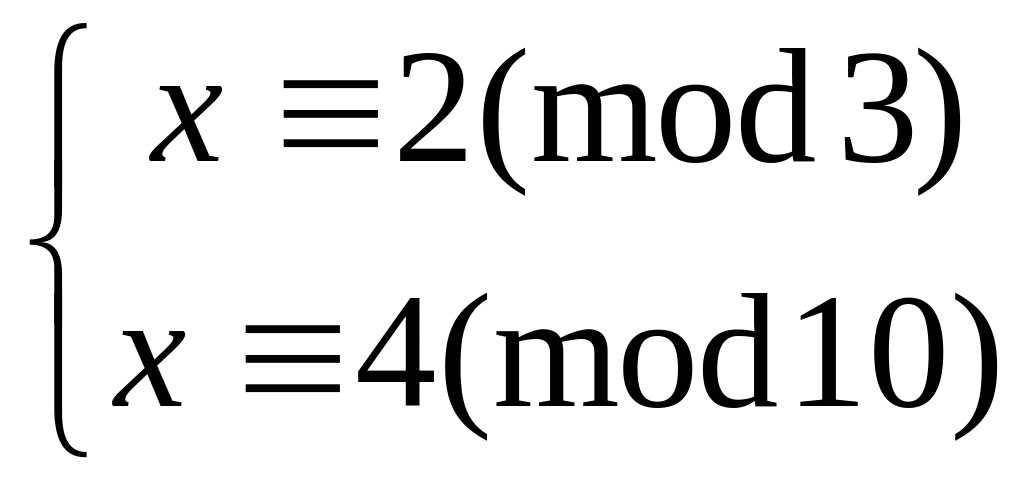
22
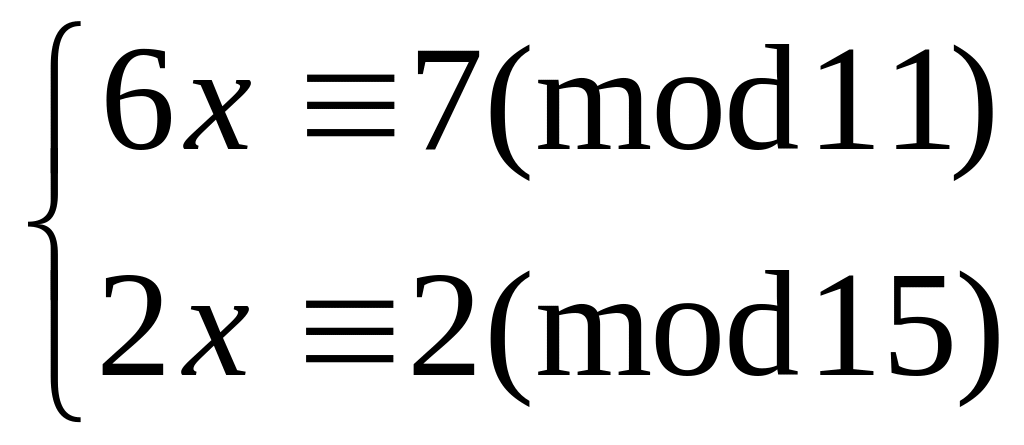
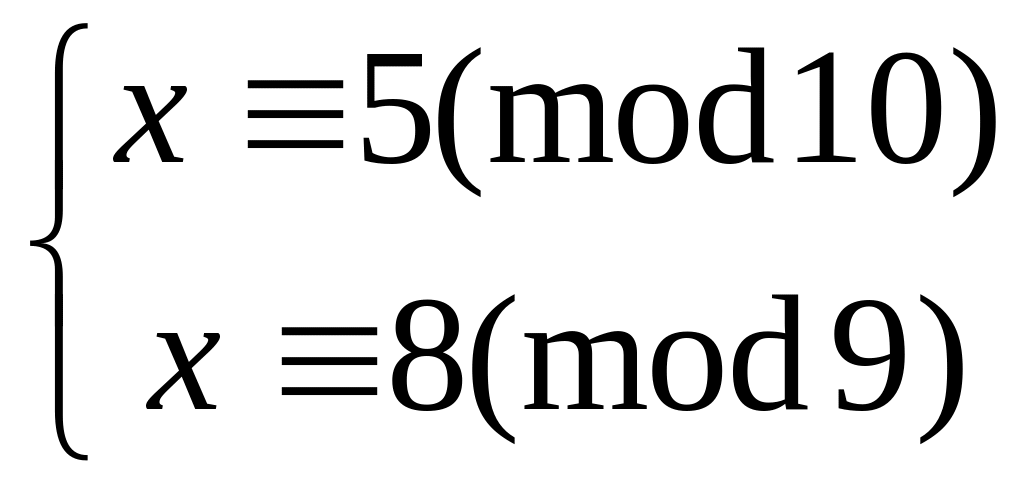
23
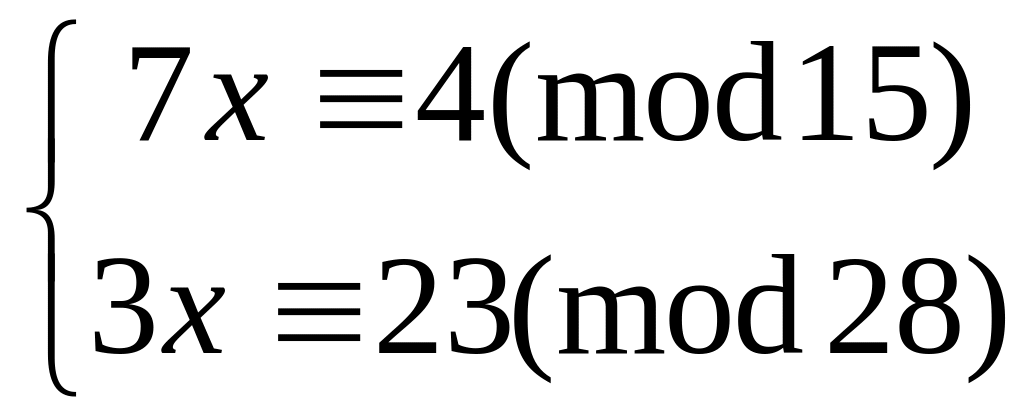
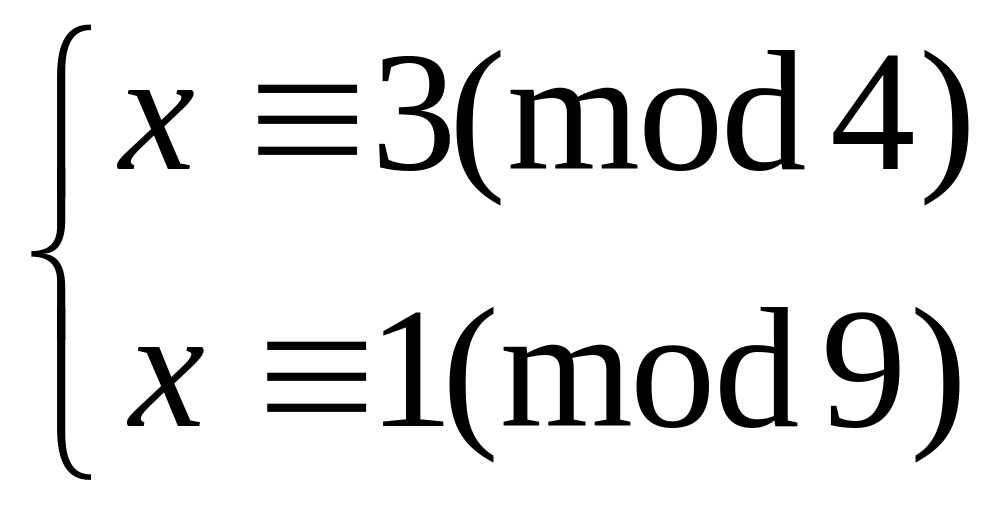
24
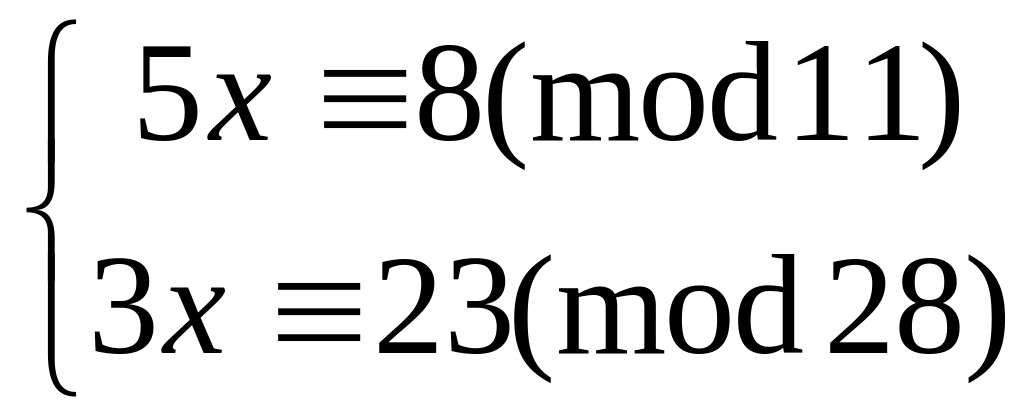
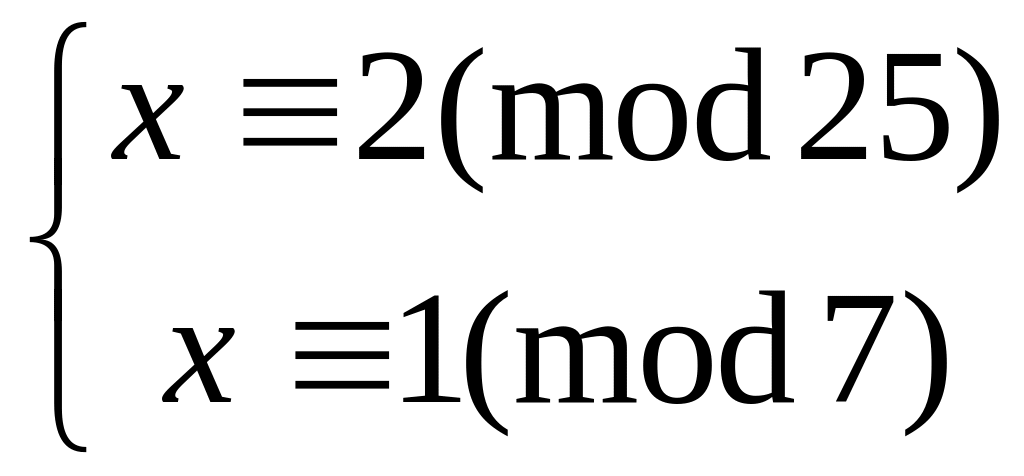
25
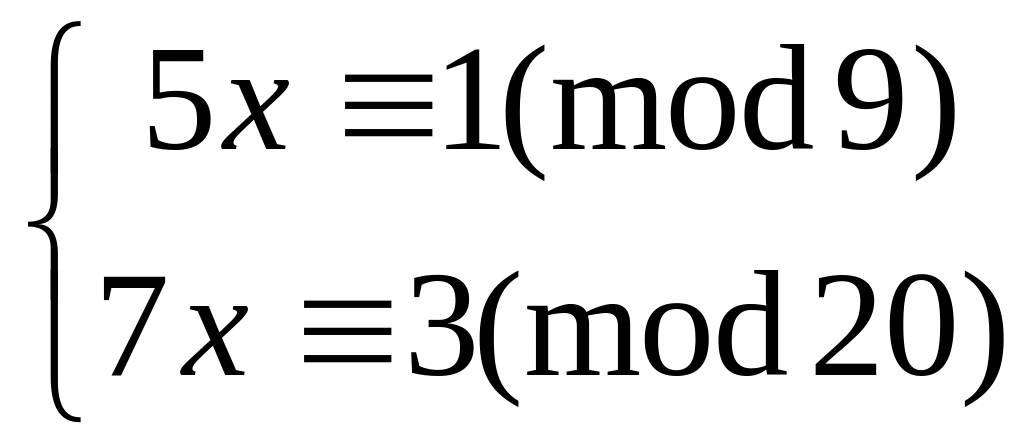
26
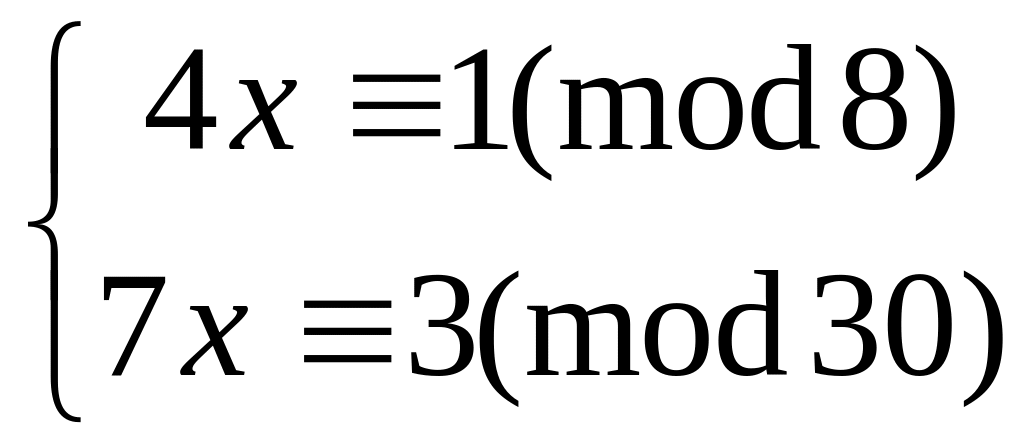
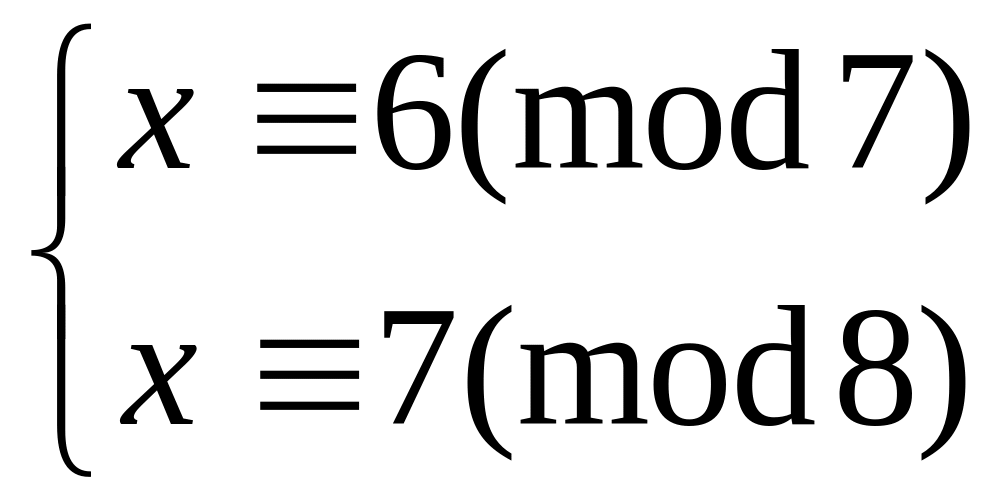
27
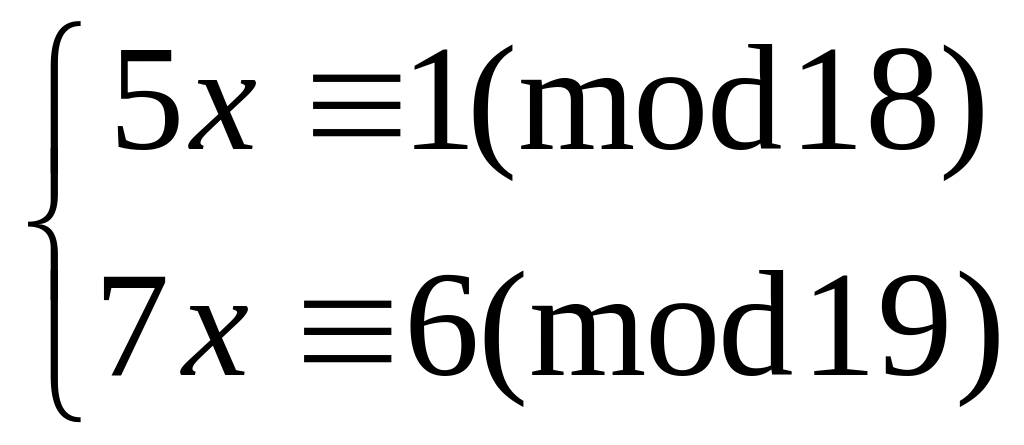
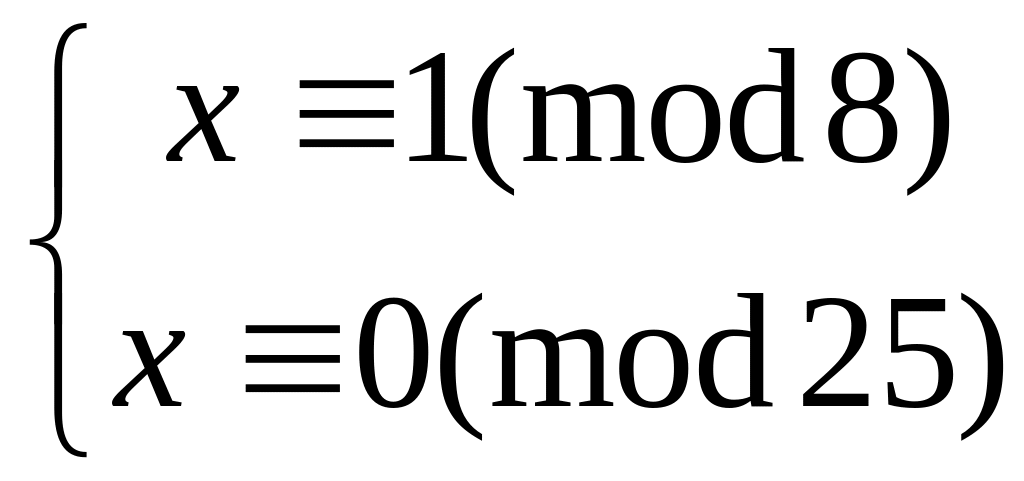
28
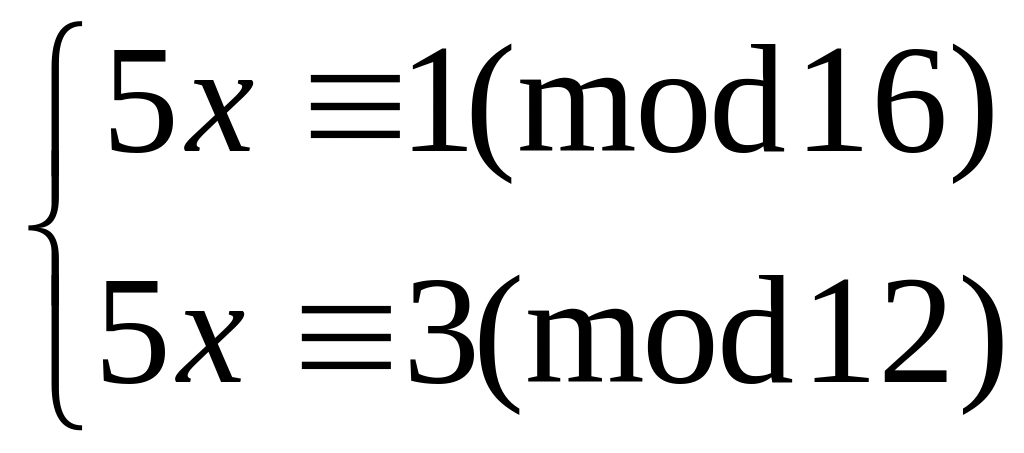
29
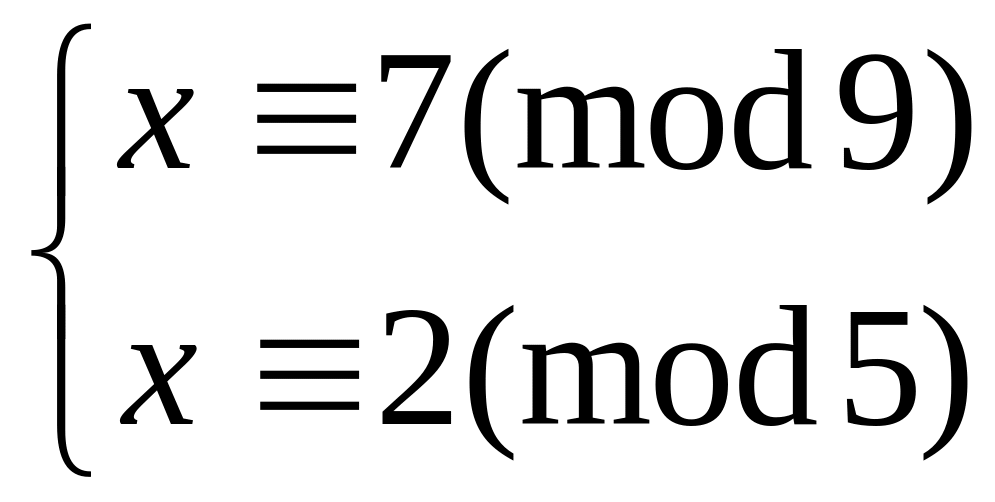
30
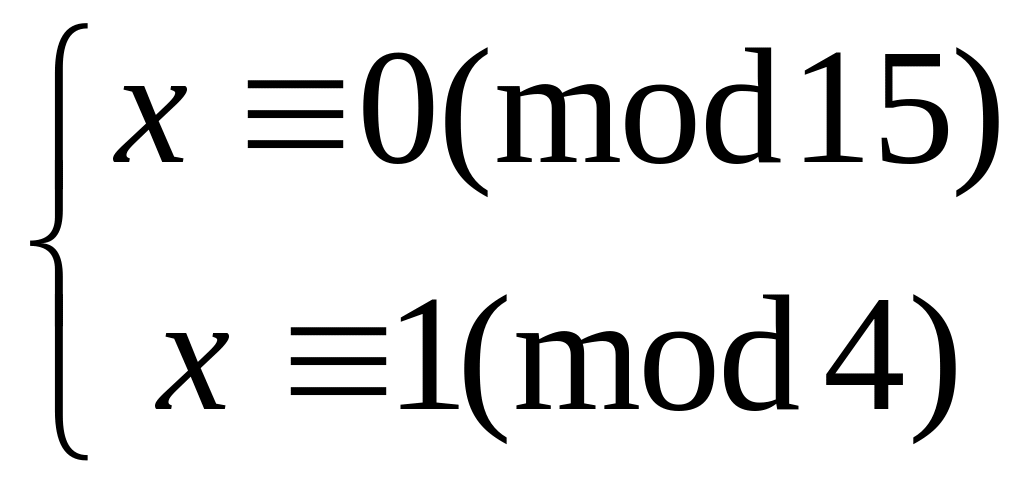
31
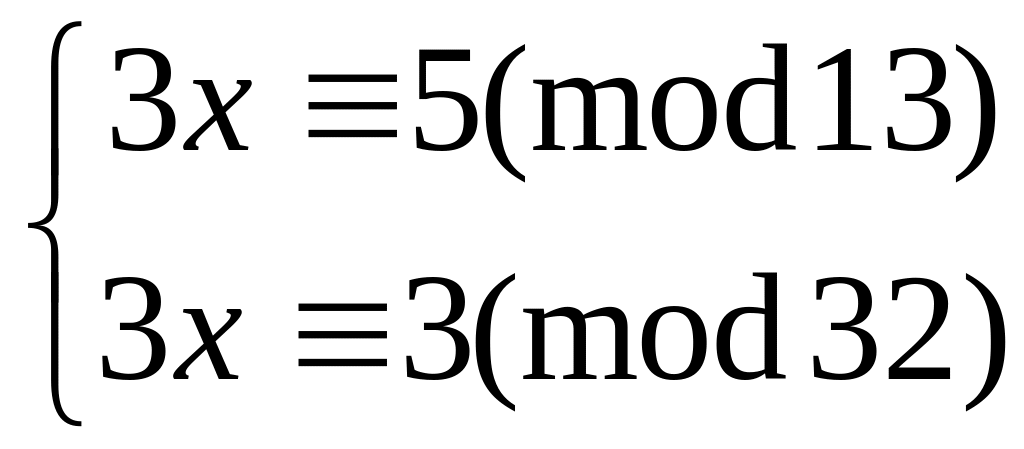
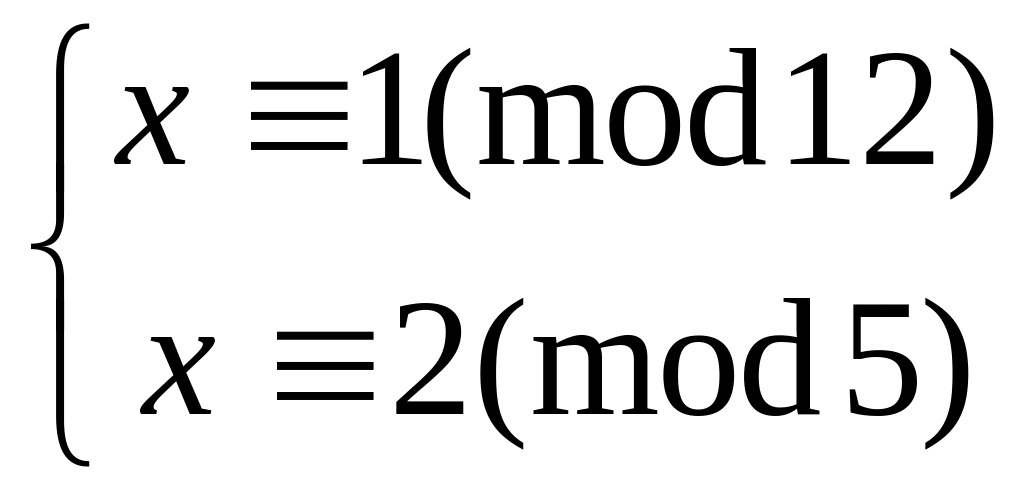
32
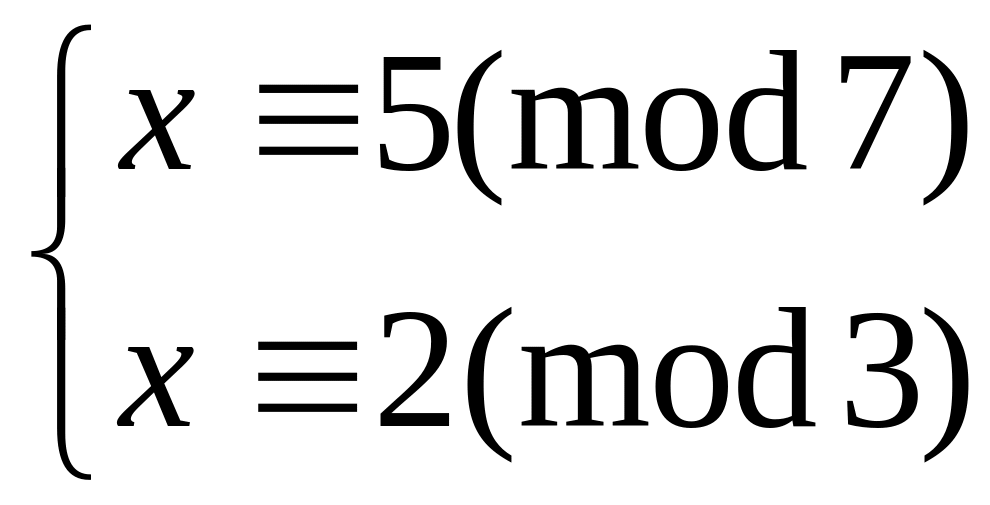
33
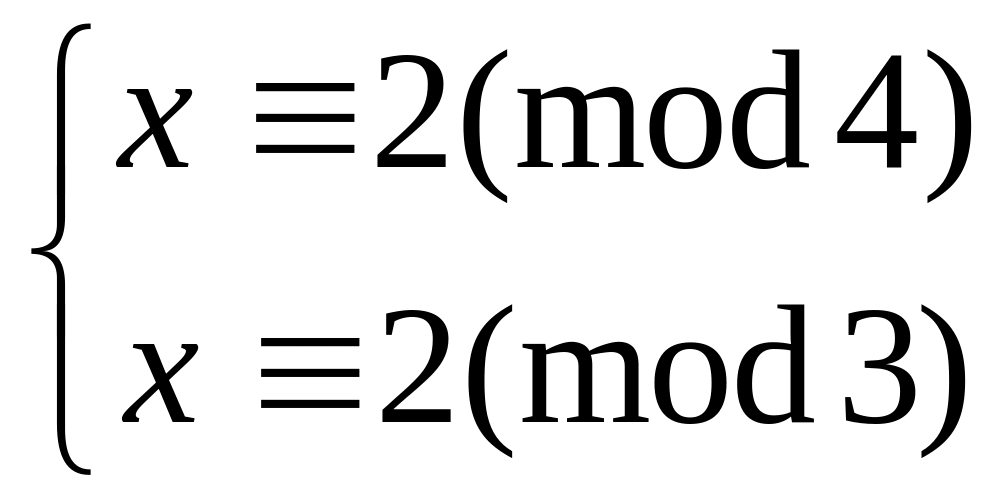
34
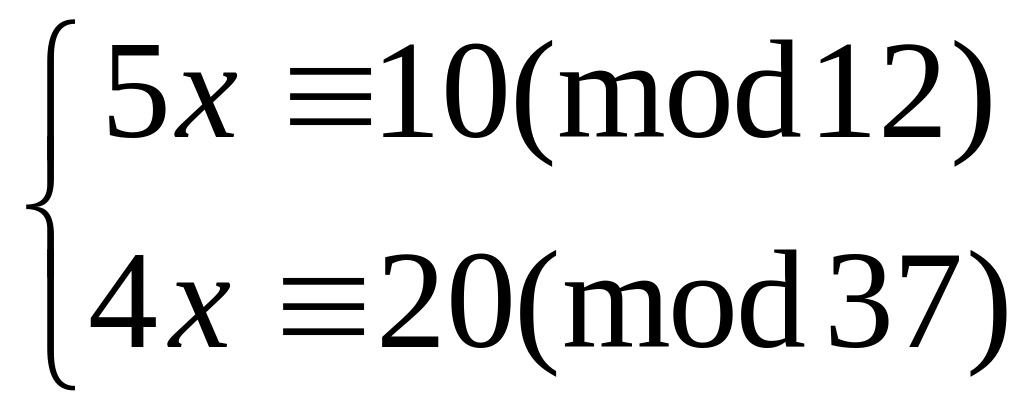
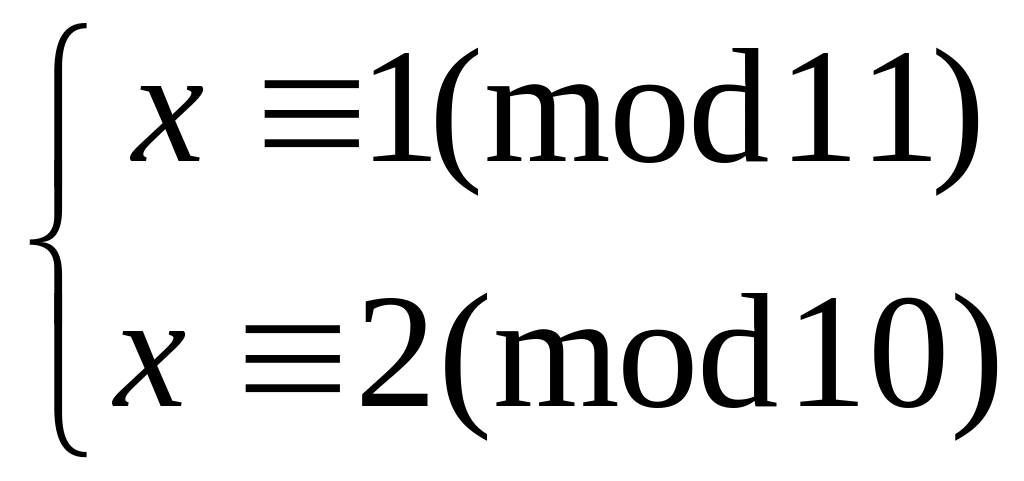
35
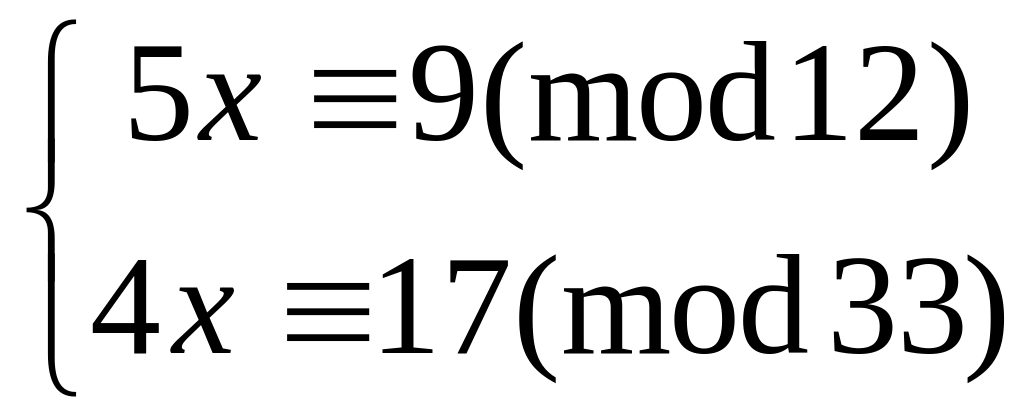
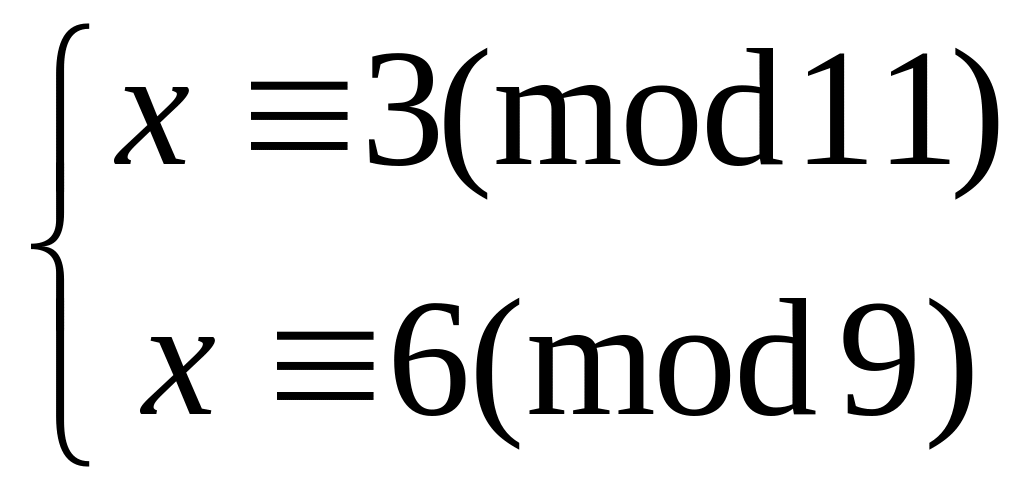
36
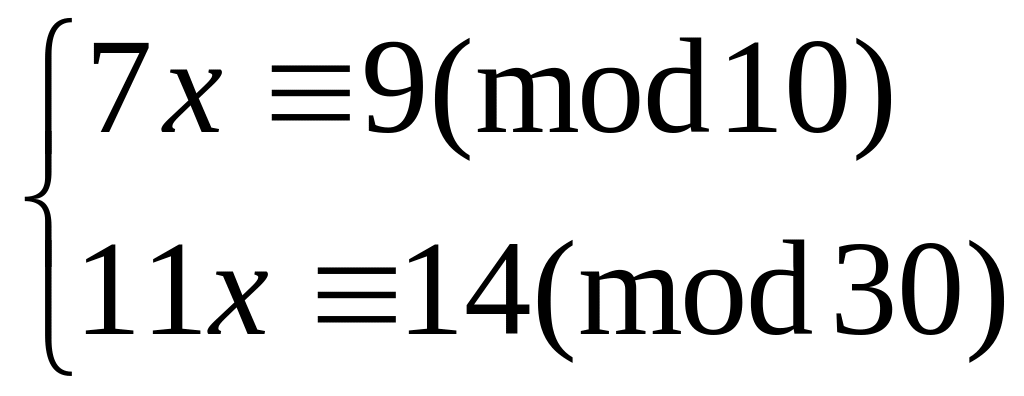
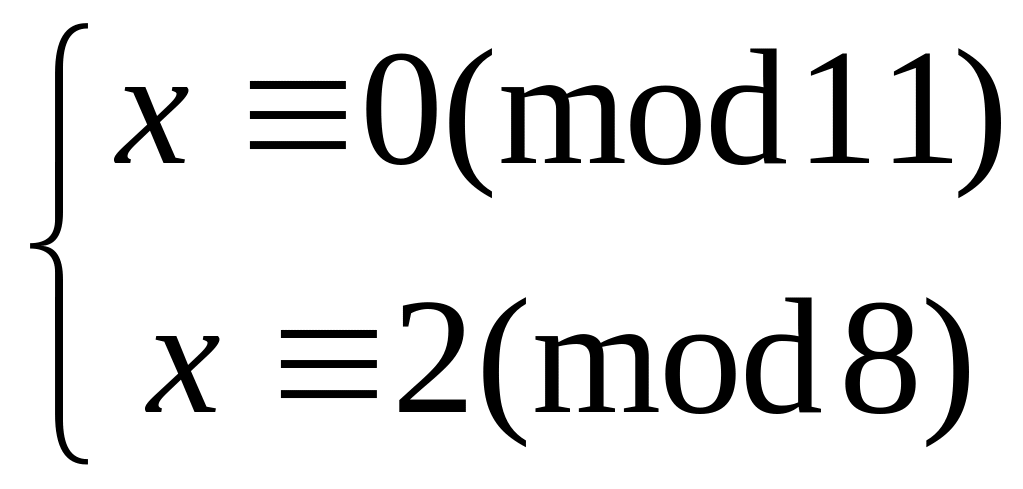
37
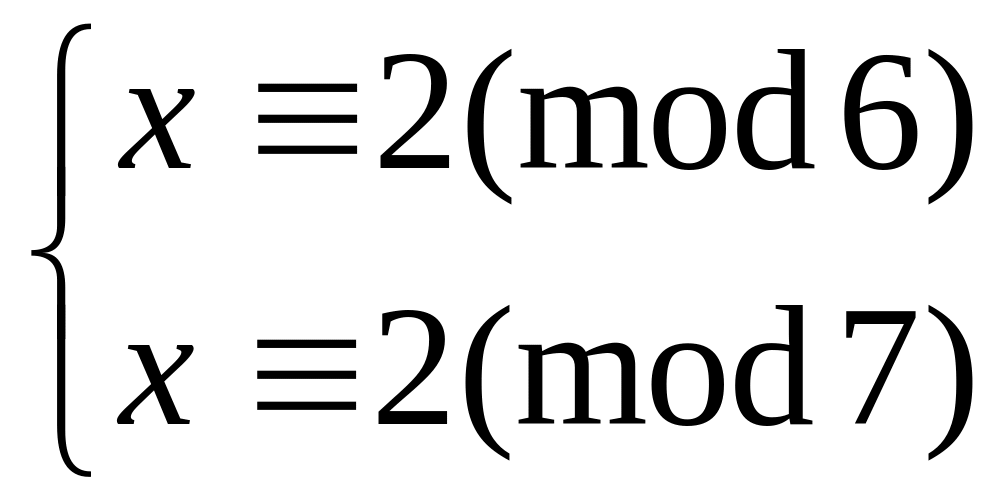
38
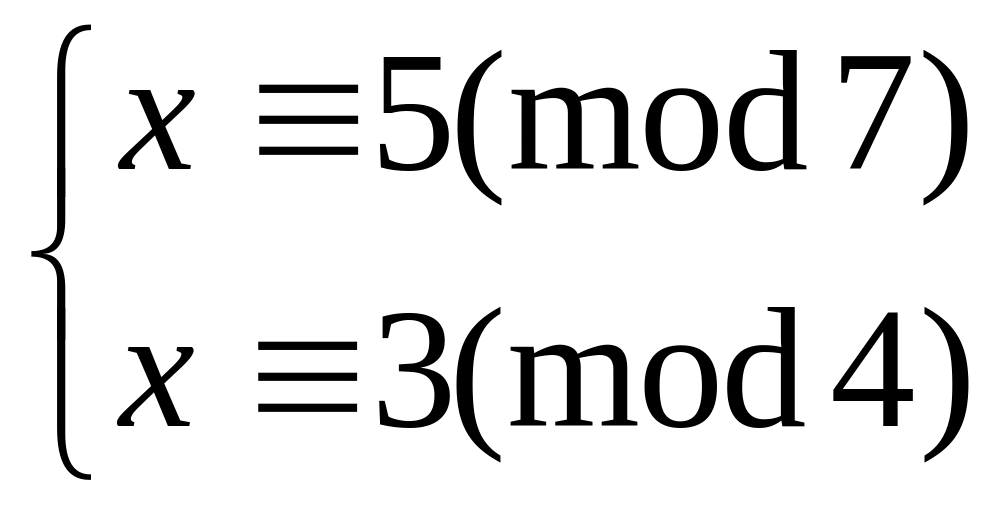
39
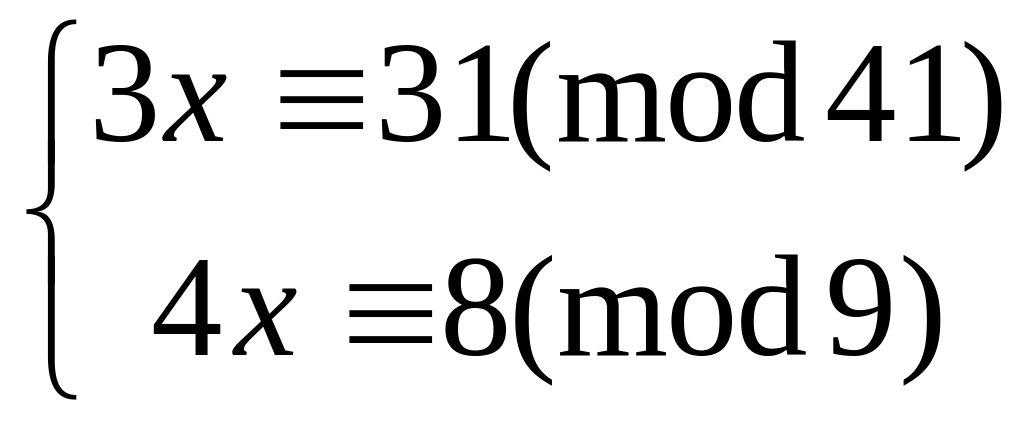
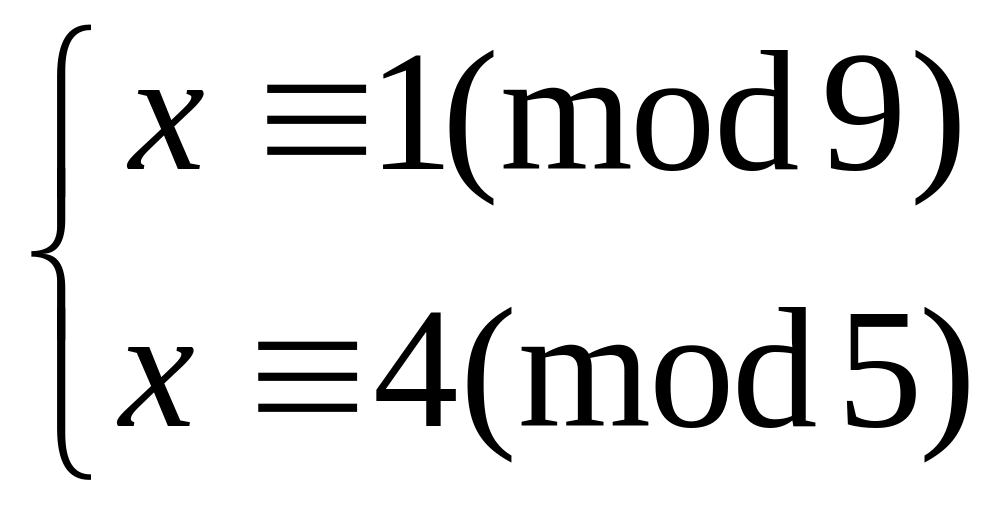
40
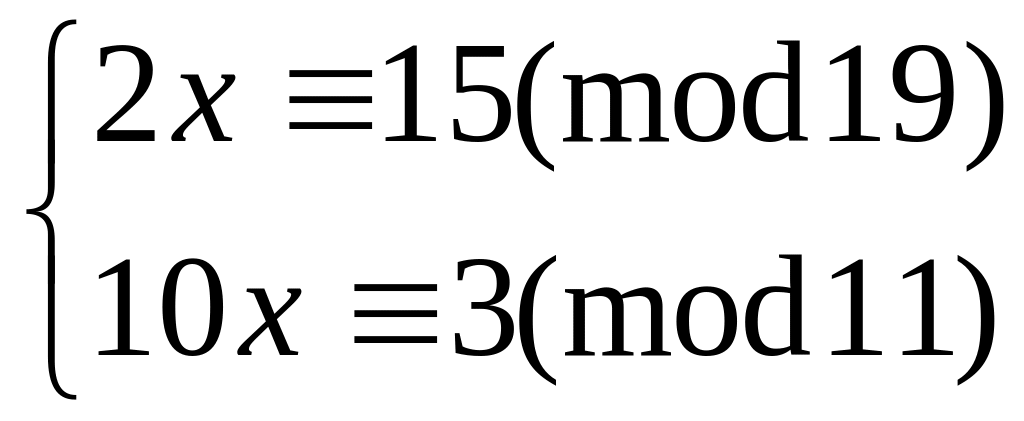
41
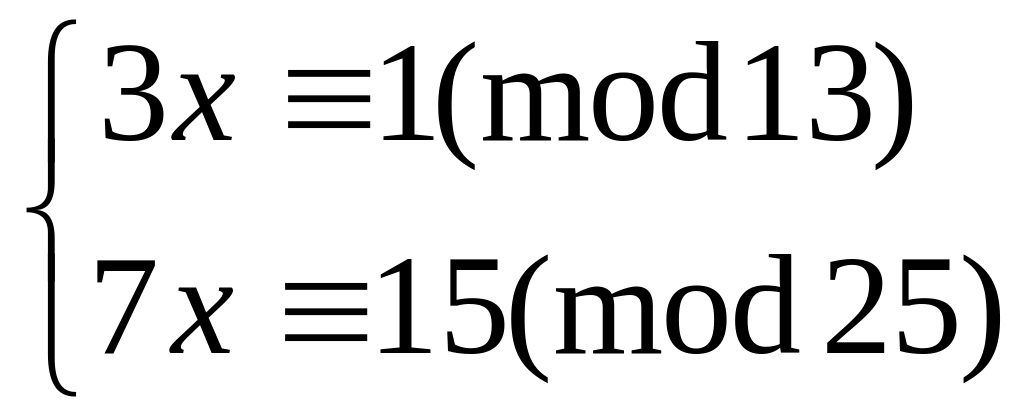
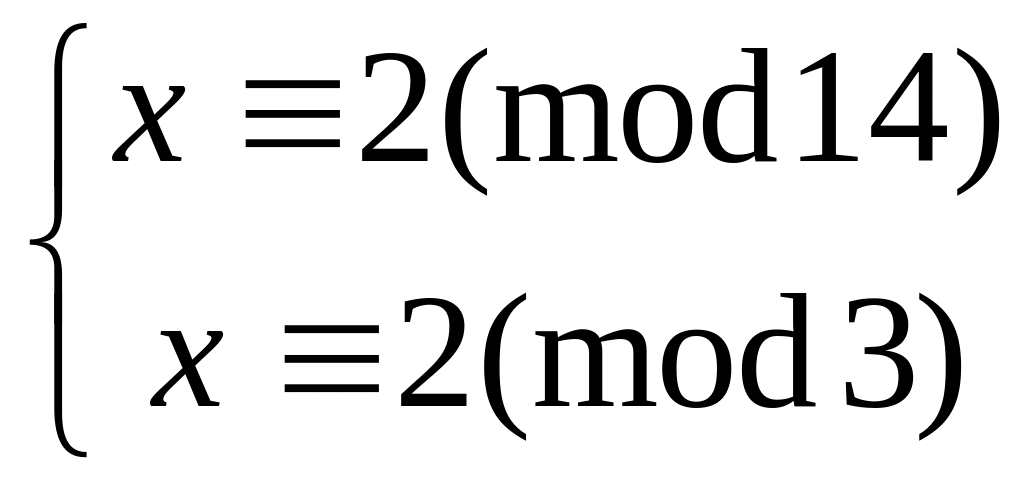
42
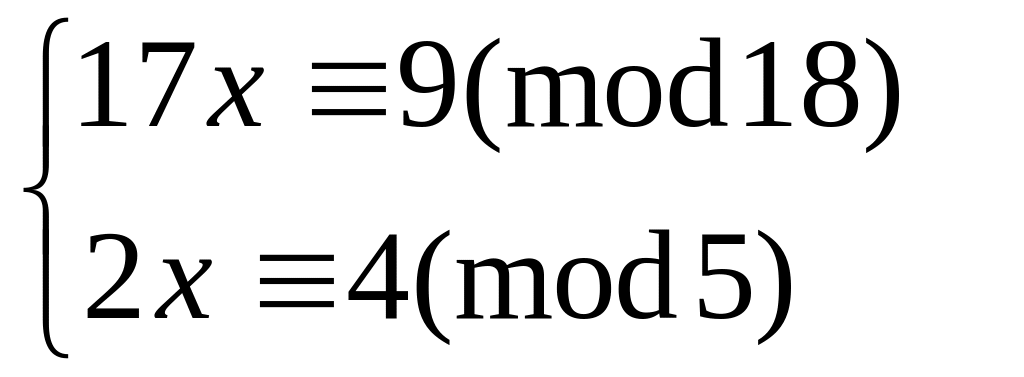
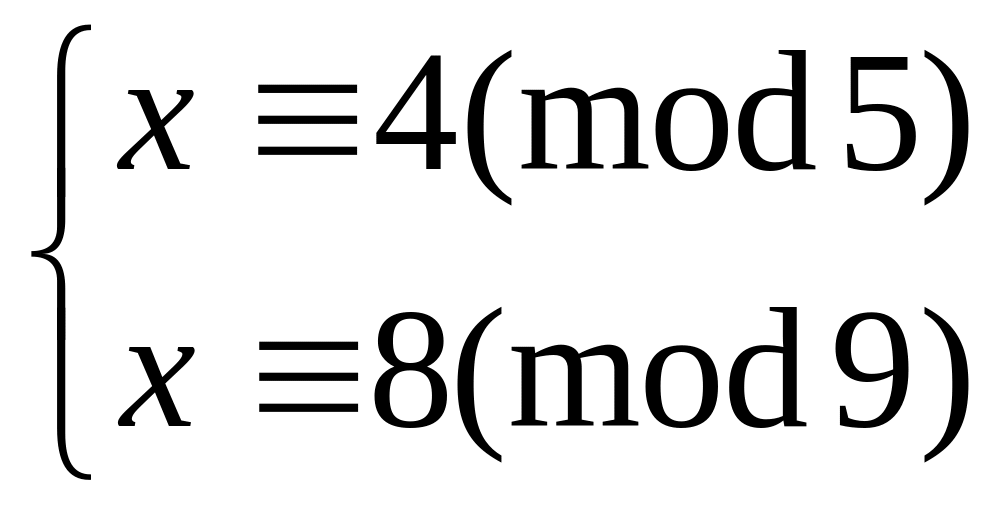
43
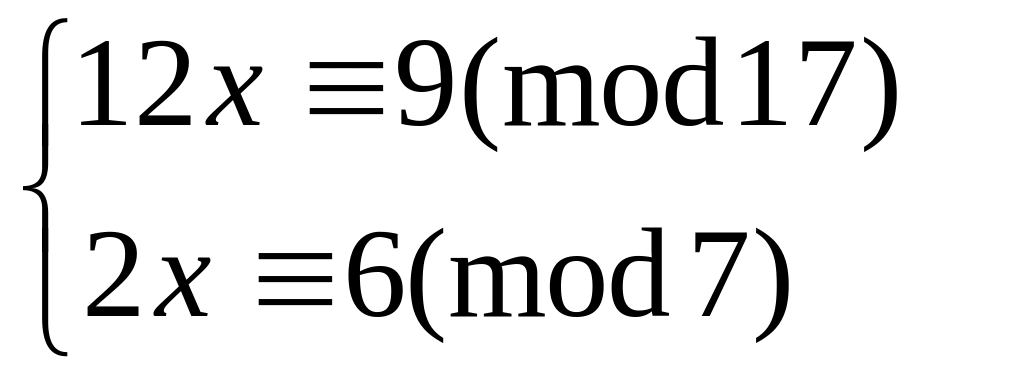
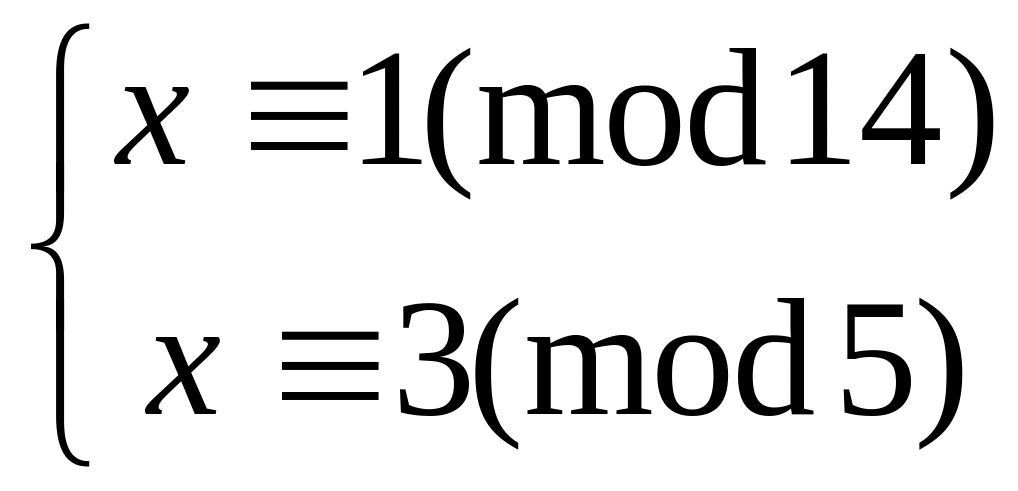
44
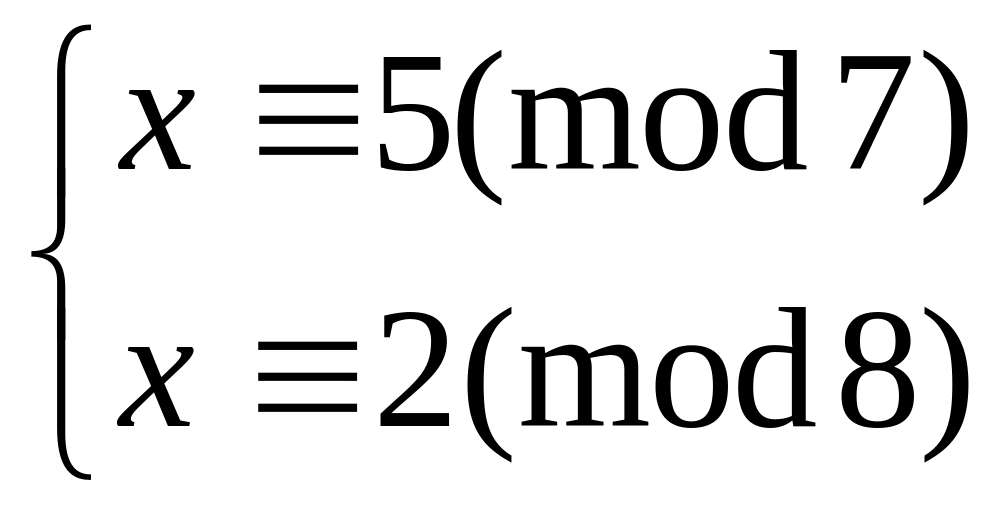
45
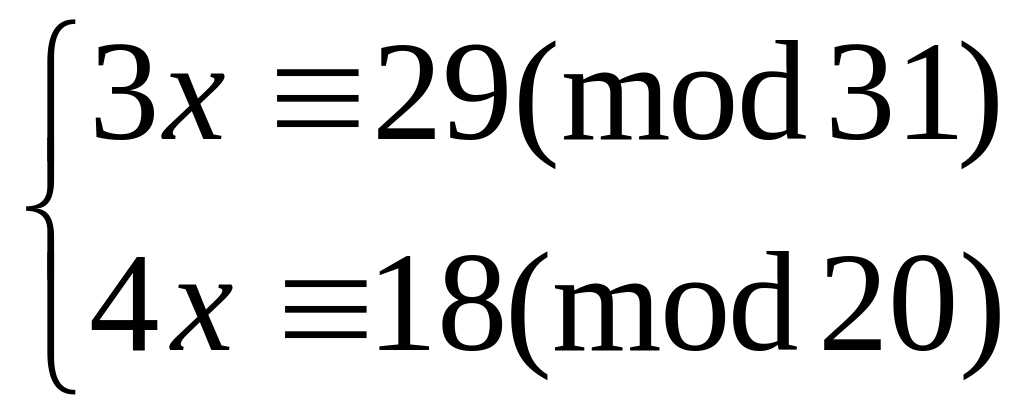
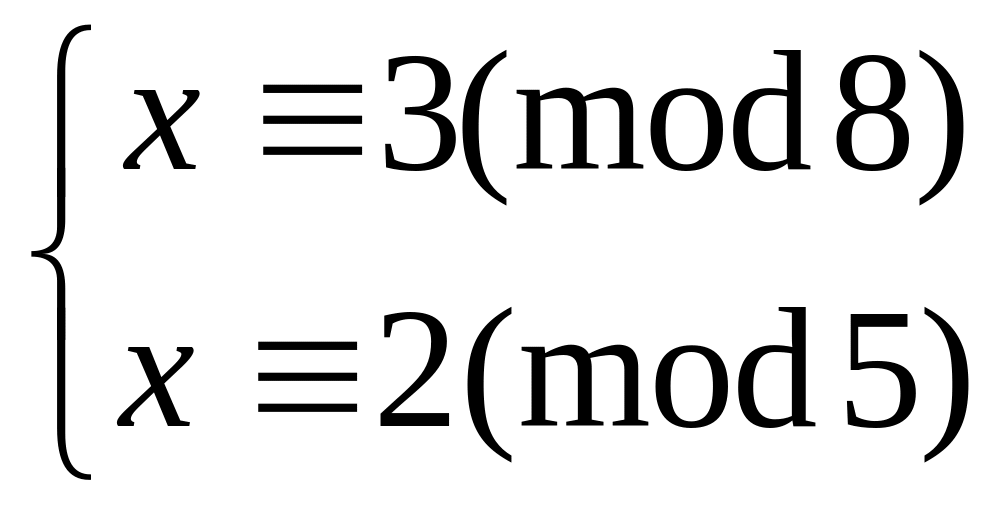
46
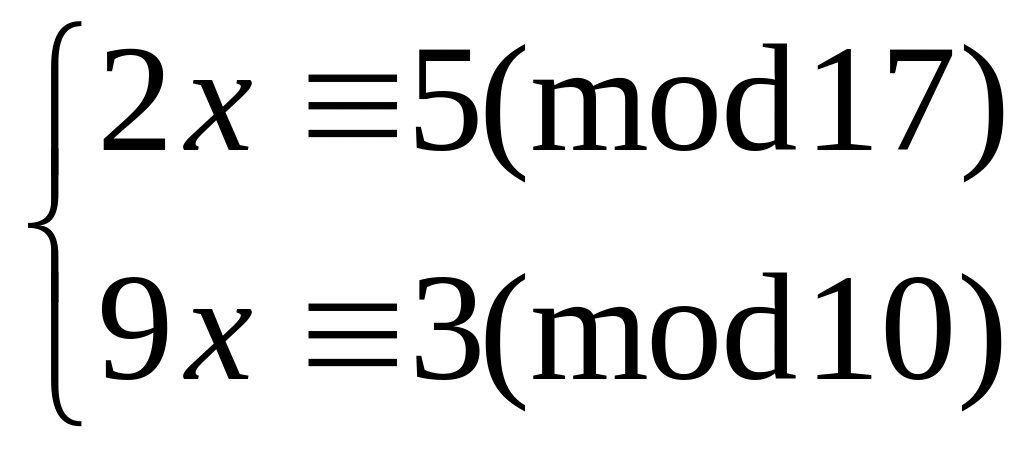
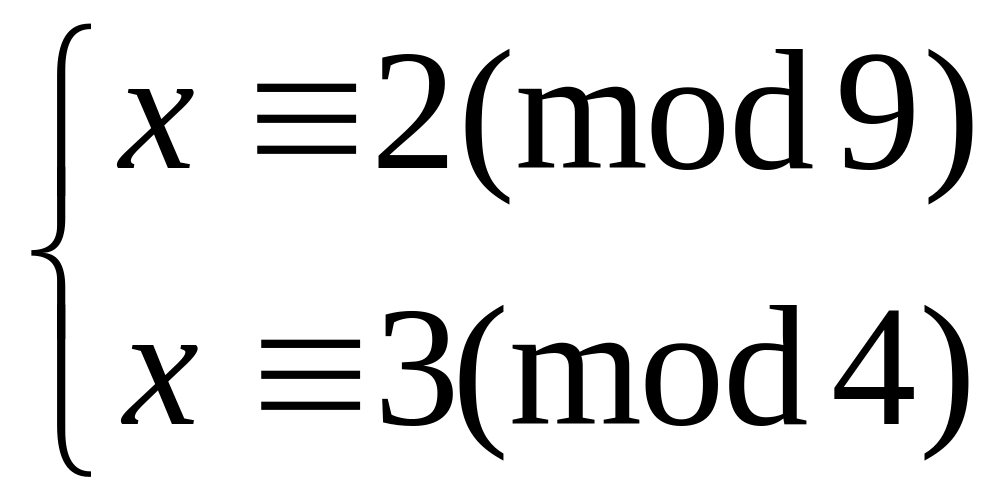
47
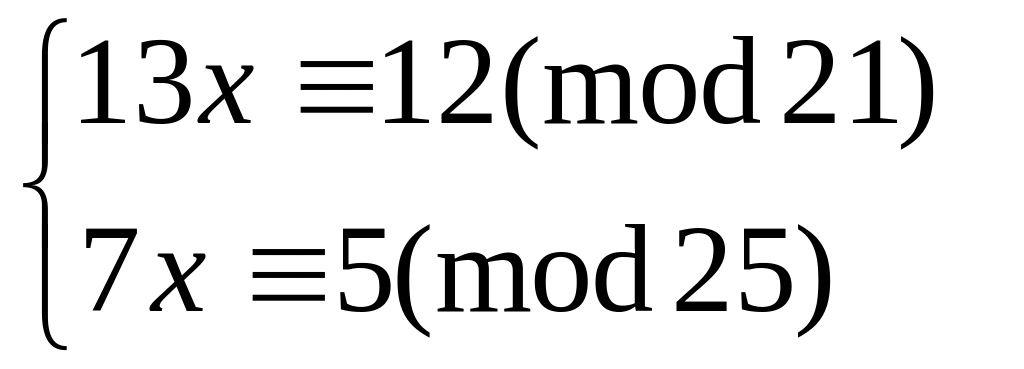
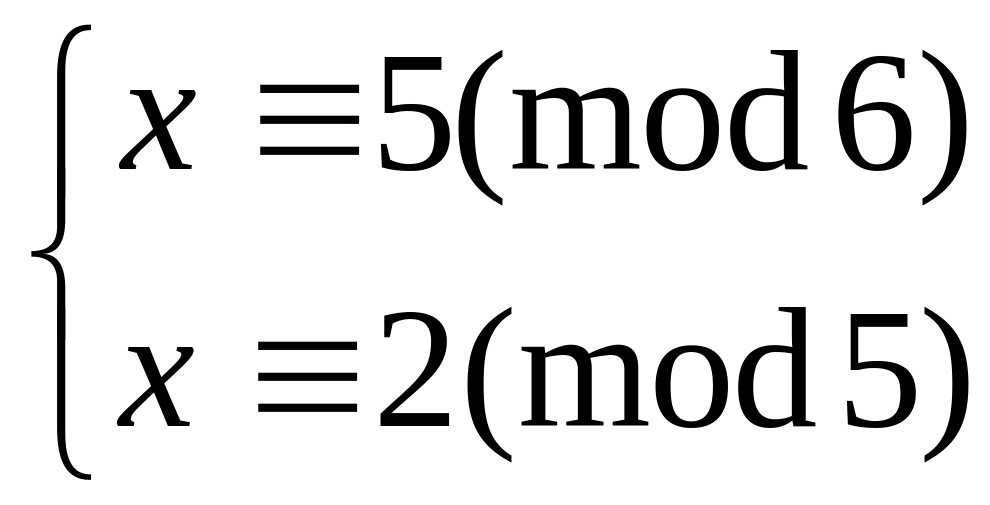
48
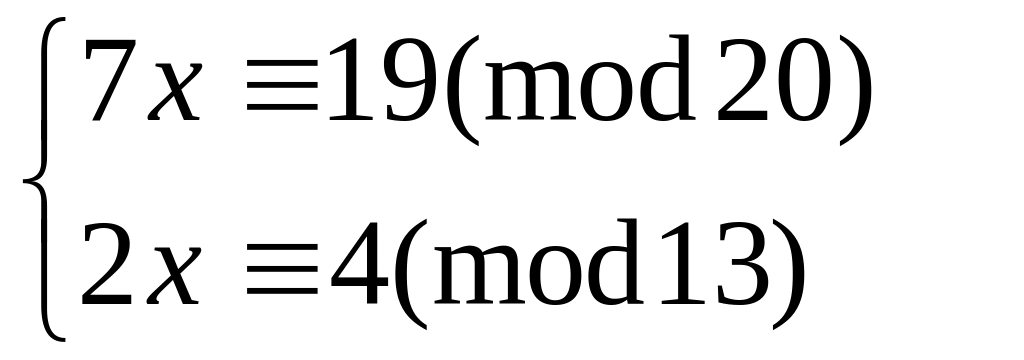
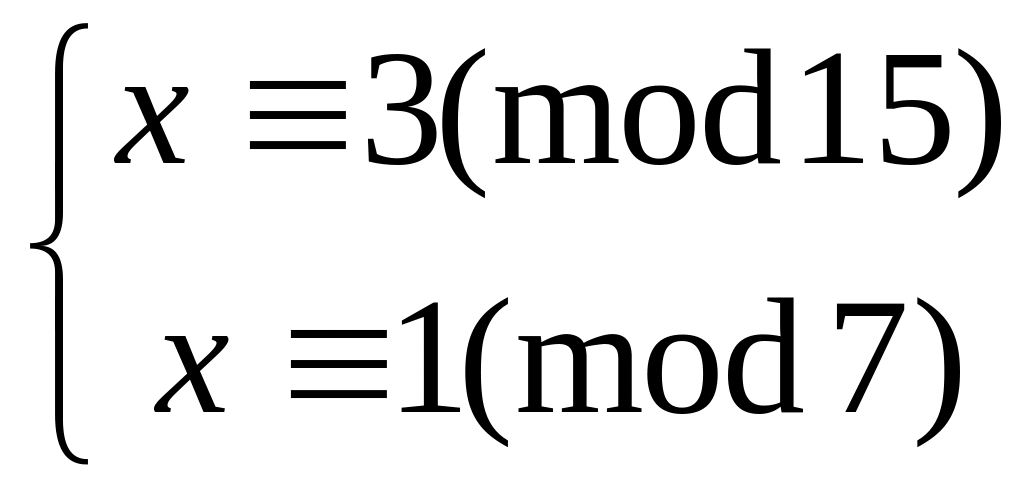
49
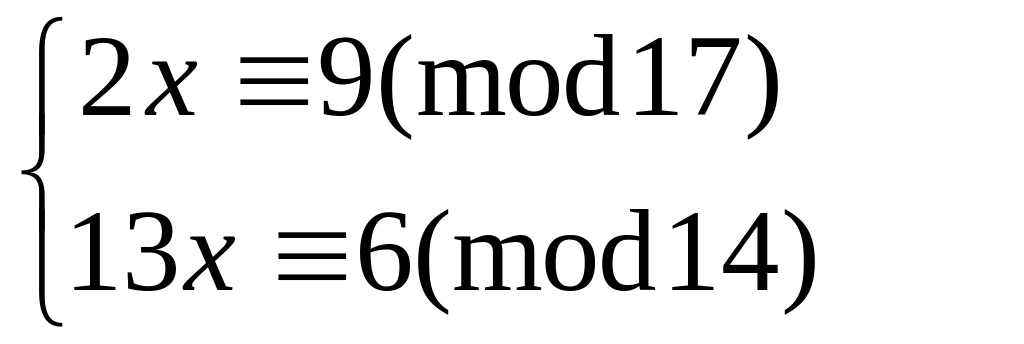
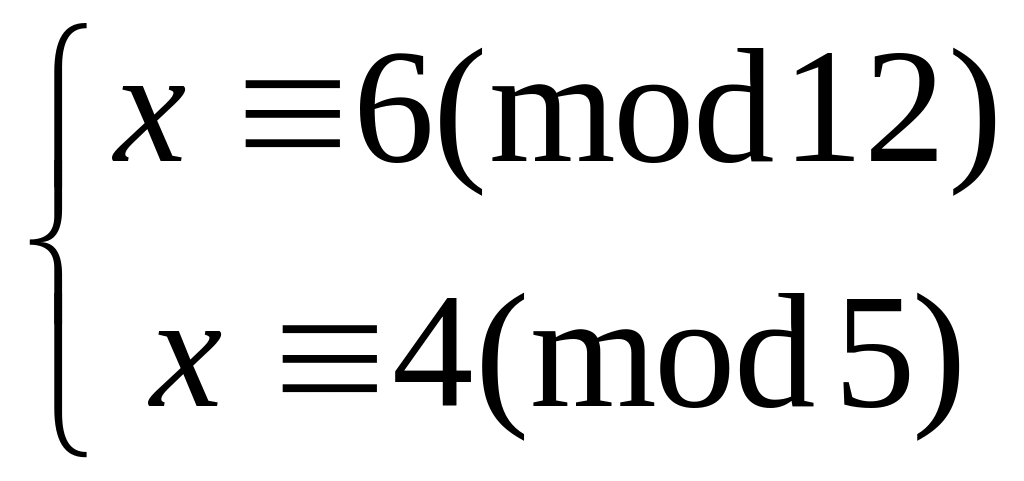
50
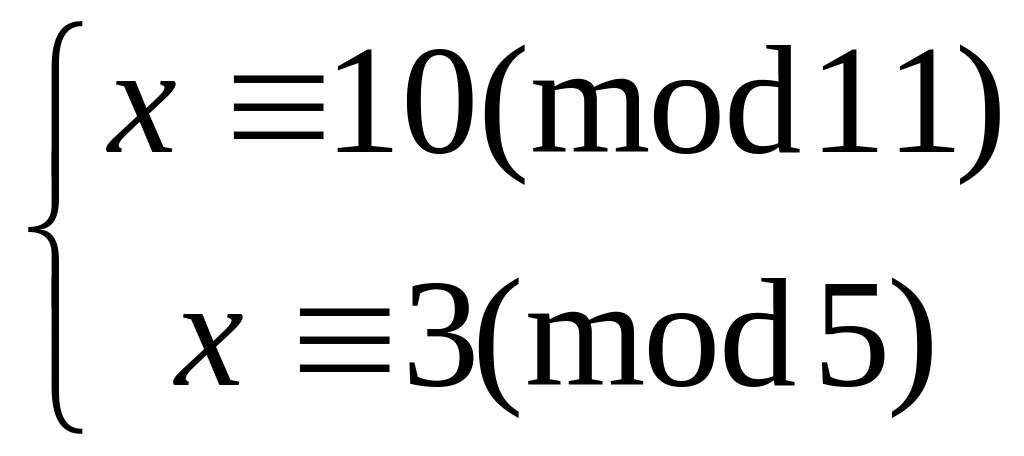
51
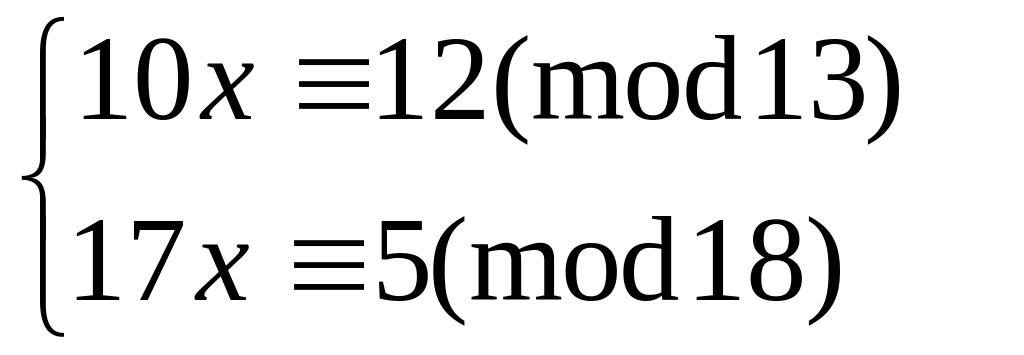
52
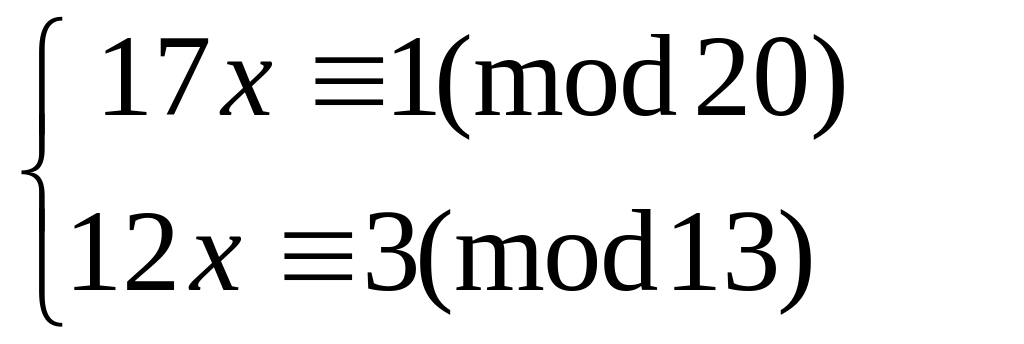
53
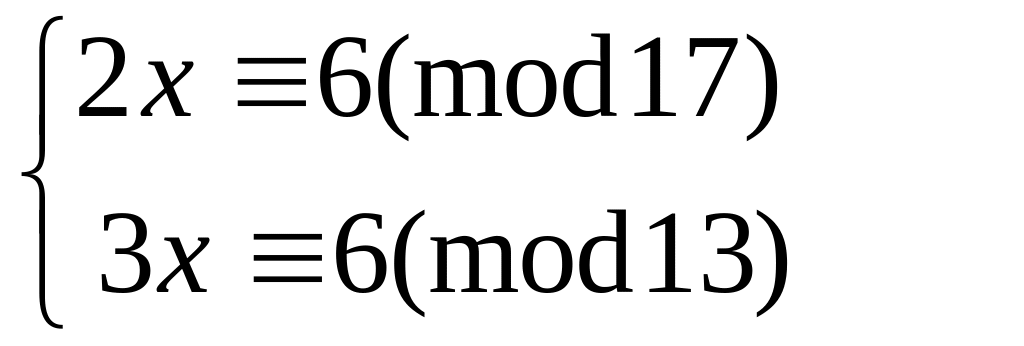
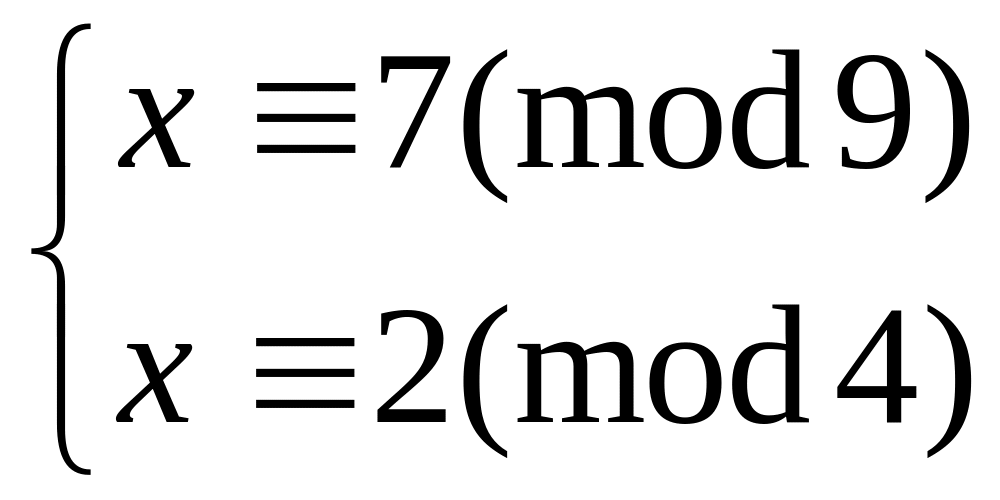
54
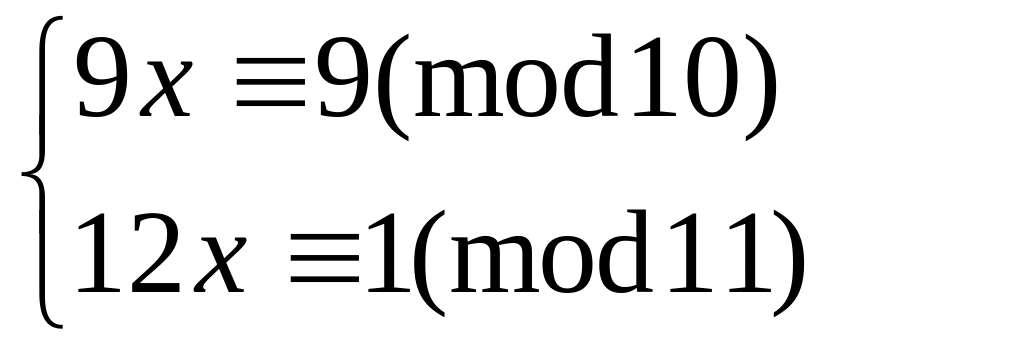
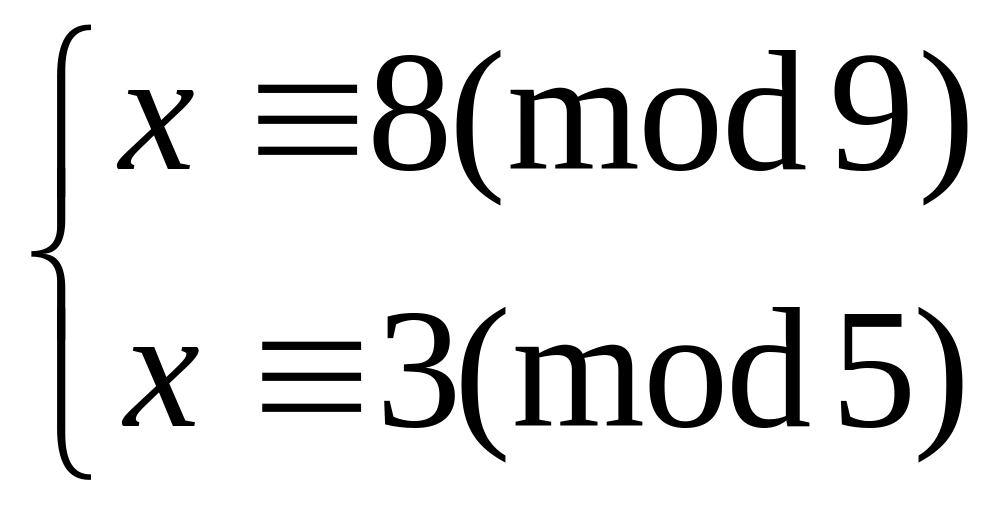
55
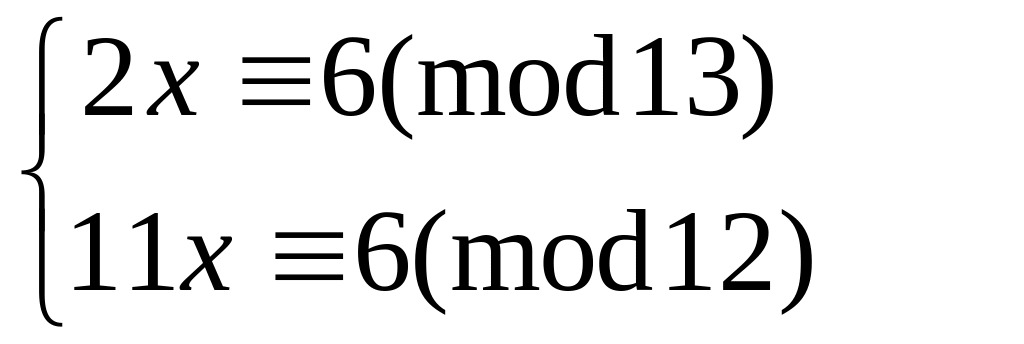
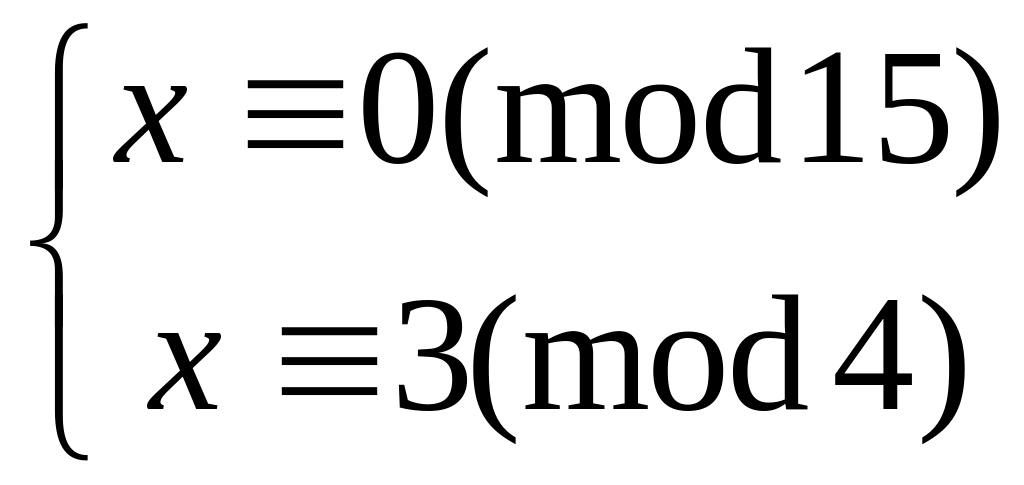
56
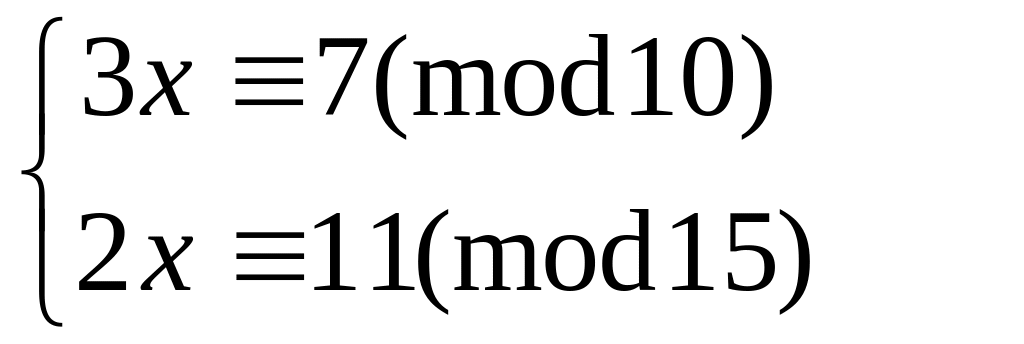
57
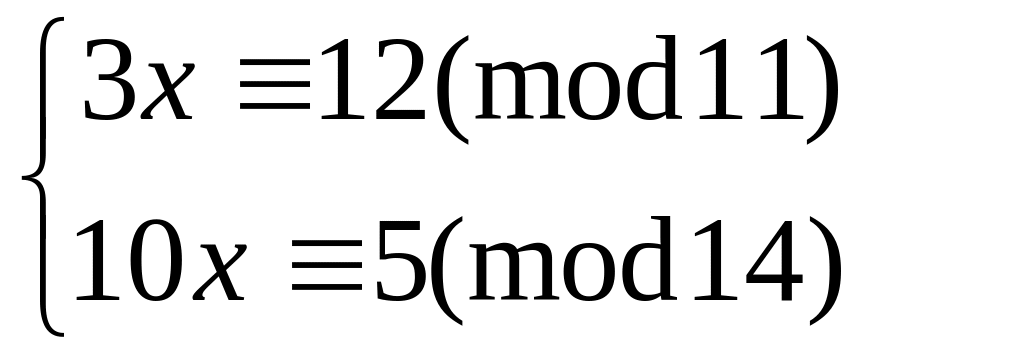
58
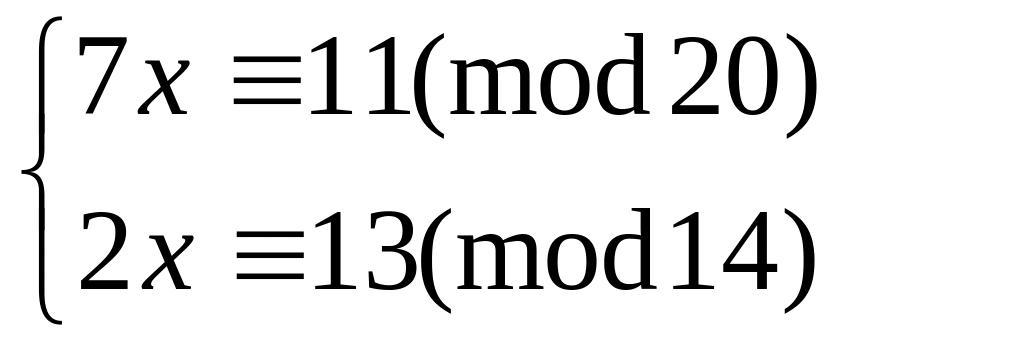
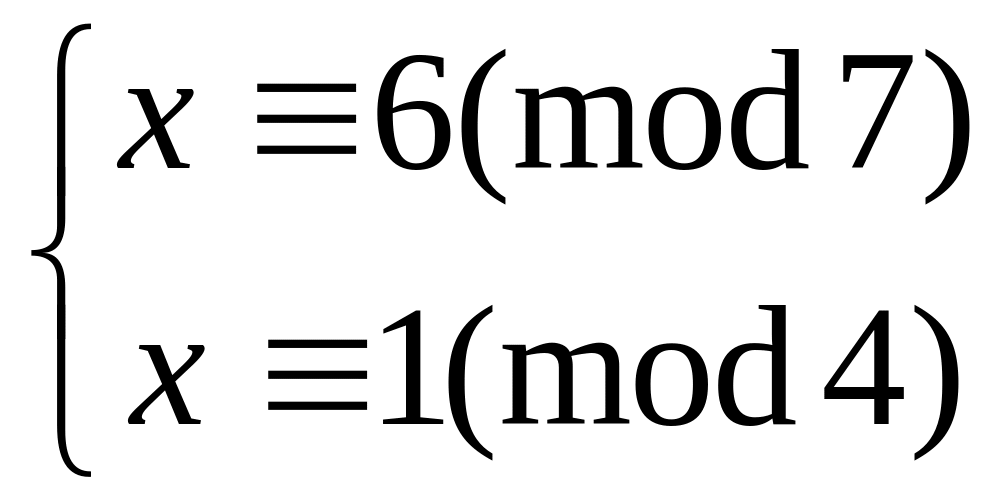
59
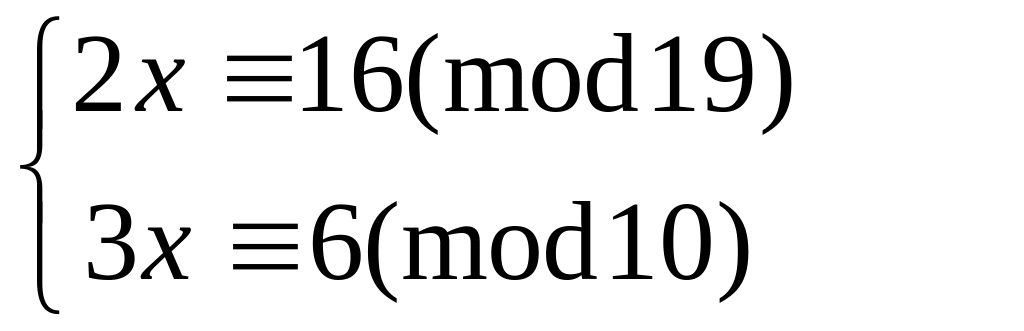
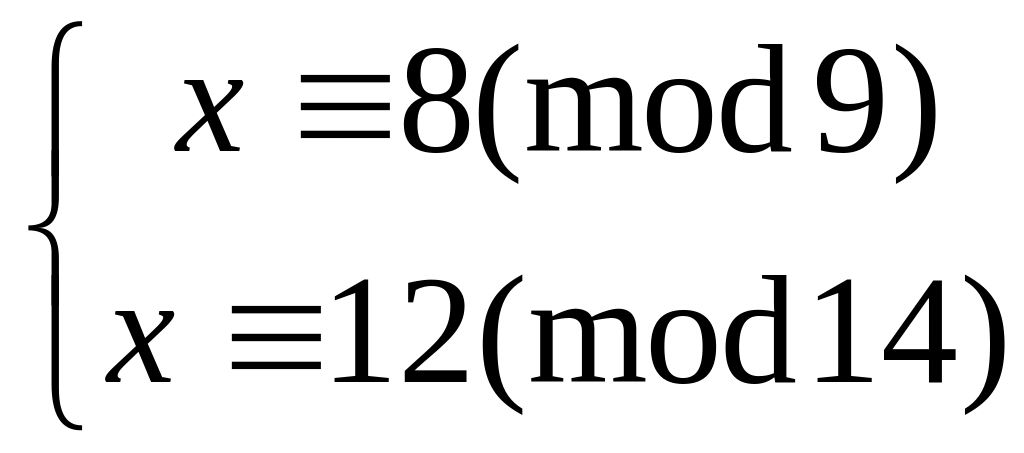
60

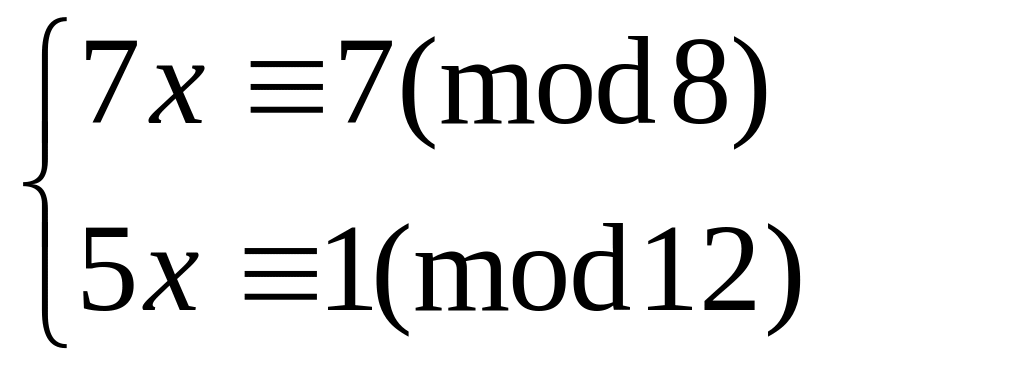
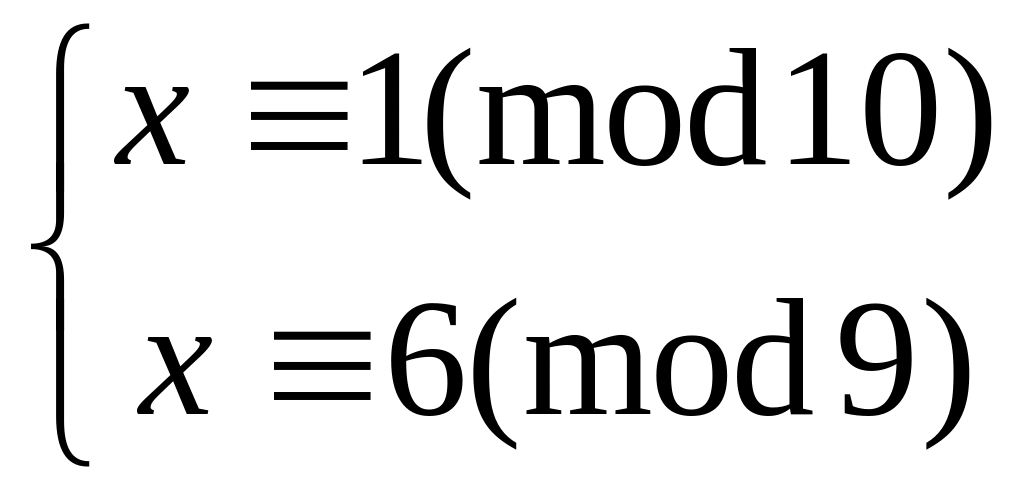
Лабораторная работа № 7. Отыскание квадратичных вычетов. Вычисление символа Лежандра. Вычисление символа Якоби.