2.1.5. Диференційна ланка із (замедлением).

Динамічні процеси в даній динамічній ланці описуються наступним диференційним рівнянням

. (2.13)

Виконавши перетворення аналогічні (2.8), одержуємо

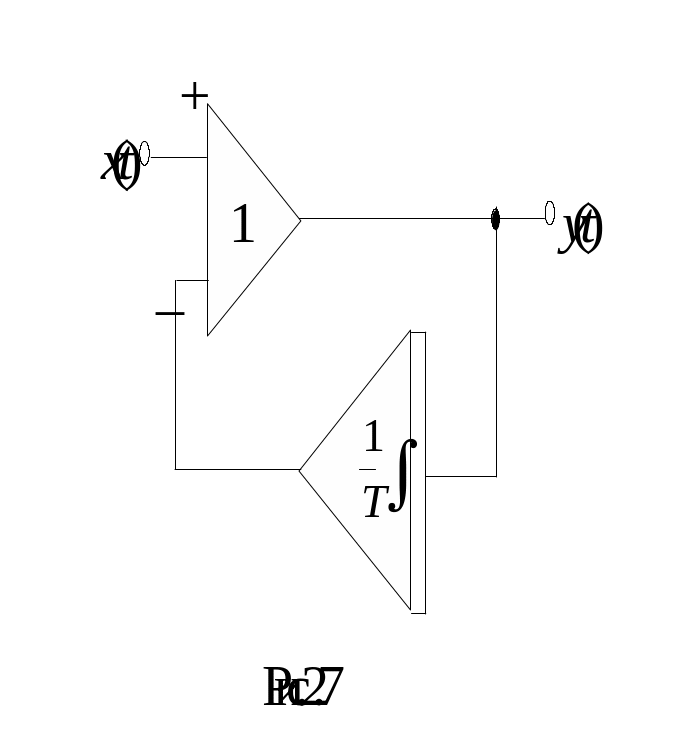
. (2.14)

Виразу (2.14) відповідає модель, що показана на рис.2.7.

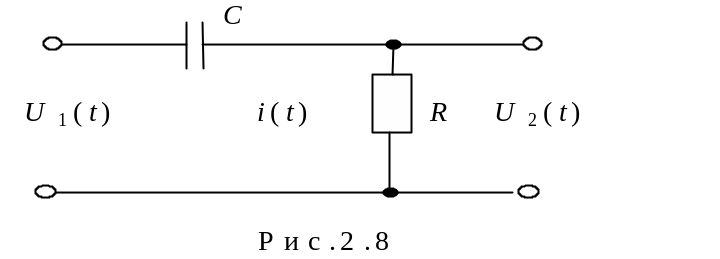
Прикладом диференційної ланки із (замедлением) є електрична схема RC- ланки, що показана на рис2.8. Процеси в цій ланці описуються системою диференційних рівнянь

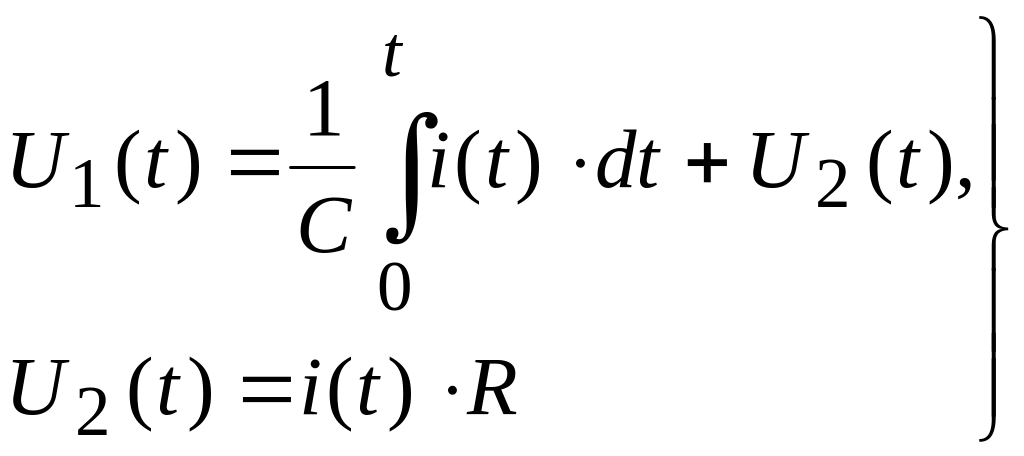. (2.15)

Розв'язавши систему рівнянь (2.15), одержуємо

, (2.16)

де T=RC.

2.1.6. Ізодромна ланка.

Динамічні процеси в ізодромній ланці описуються наступними диференційними рівняннями

. (2.17)

Проінтегрувавши і розділивши на Т₁ обидві частини рівняння (2.17), одержуємо

. (2.18)

Виразу (2.18) відповідає модель (рис.2.9) ізодромної ланки і якій К=Т₂/Т₁.

2.1.7. Коливальна ланка.

Диференційне рівняння коливальної ланки має вигляд

(2.19)

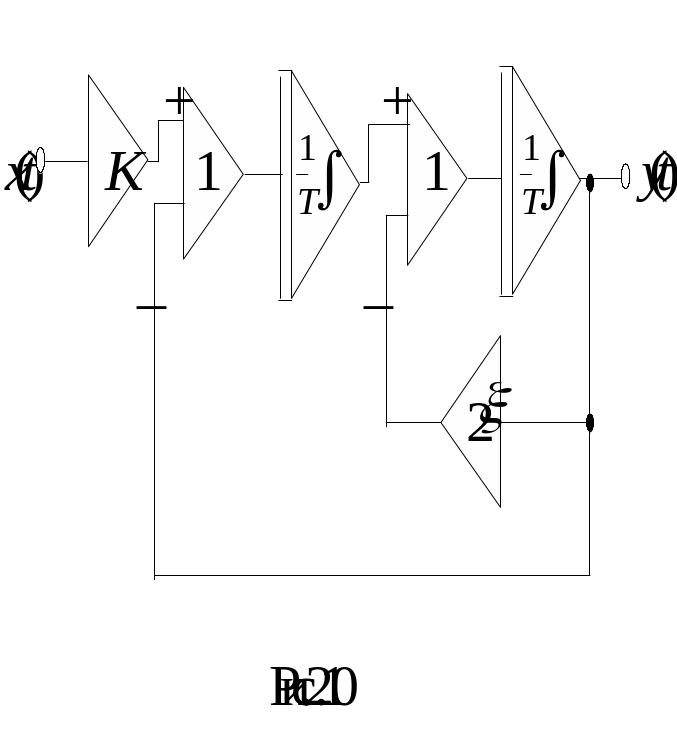Представивши (2.11) в вигляді аналогічному (2.8), одержимо модель (рис.2.6) коливальної ланки.

Прикладом коливальної ланки є електричний ланцюг принципова схема якого наведена на рис.2.11.

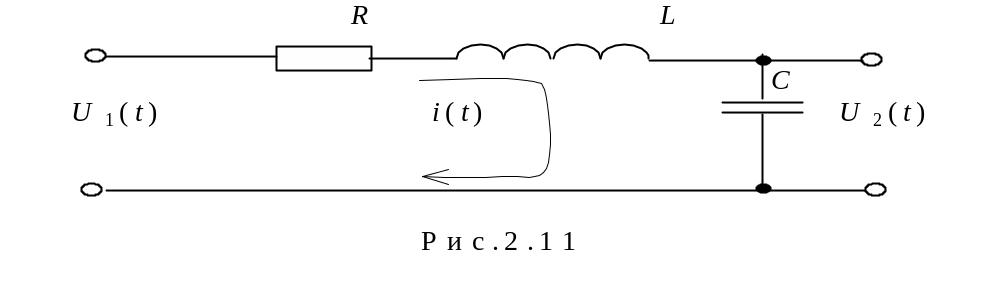
Розв'язавши систему рівнянь (2.20), одержуємо

Наведеній схемі відповідає наступна система диференційних рівнянь

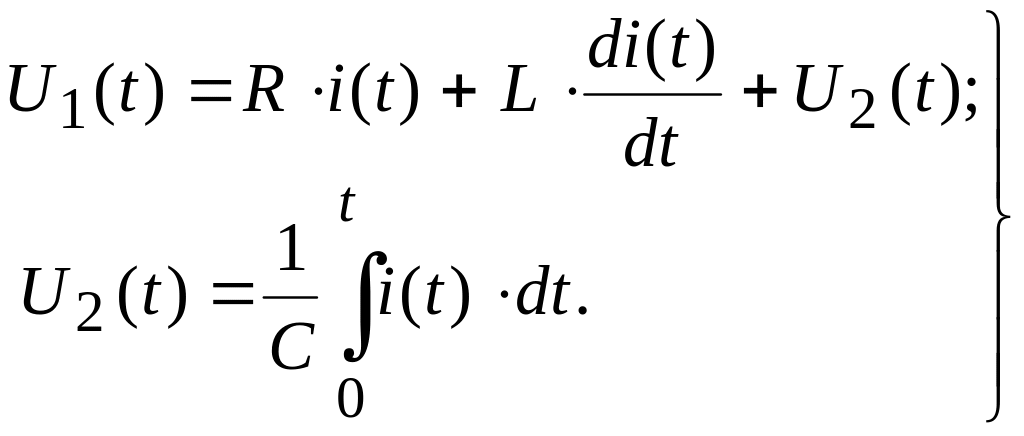(2.20)