2. Динамічні характеристики систем автоматичного регулювання

1. Диференційні рівняння динамічних ланок системи автоматичного регулювання

В відміну від усталеного режиму, динамічний режим характеризується змінами вхідного та вихідного сигналів: x(t)=var, y(t)=var. Поведінка системи автоматичного регулювання в динамічному режимі описується диференційними рівняннями п-го порядку

(2.1)

де т  п+1.

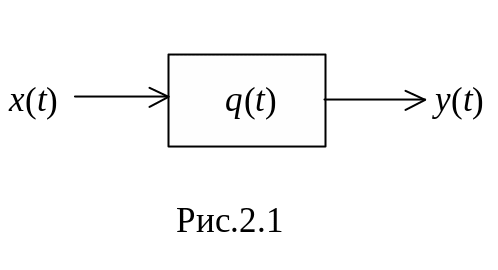Розглянемо динамічну ланку (рис.2.1), динамічні процеси якої описуються функцією q(t). В залежності від виду функції q(t) змінюються динамічні властивості ланки.

2.1.1. Пропорційна ланка.

Для пропорційної ланки q(t)=К. Диференційне рівняння пропорційної ланки має вигляд

. (2.2)

2.1.2. Диференційна ланка.

В цій динамічній ланці функція q(t) описує процес диференціювання в

часі вхідного діяння. Диференційне рівняння диференційної ланки має вигляд

, (2.3)

де Т- стала часу.

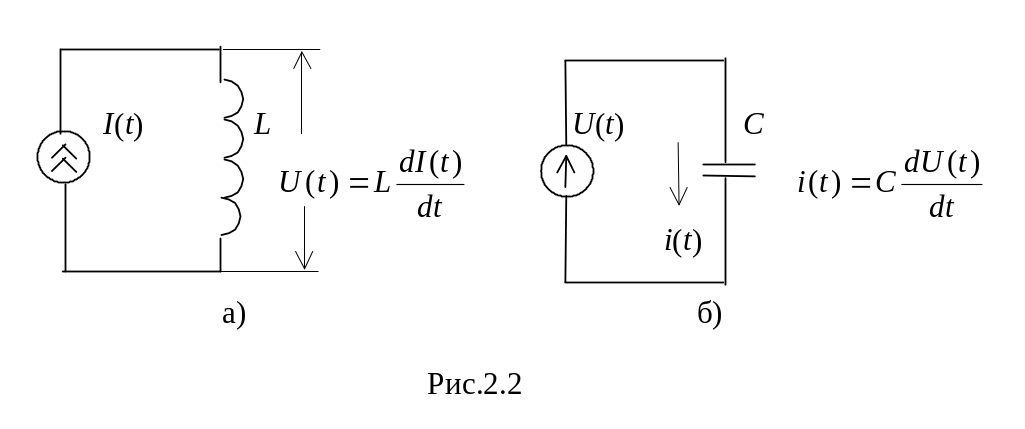Прикладами диференційних ланок є підключення індуктивності L (рис.2.2,а) до джерела струму I(t) та підключення конденсатора С (рис.2.2,б) до джерела напруги U(t).

2.1.3. Інтегруюча ланка.

В даній динамічній ланці функція q(t) описує процес інтегрування вхідного діяння. Диференційне рівняння інтегруючої ланки має вигляд

. (2.4)

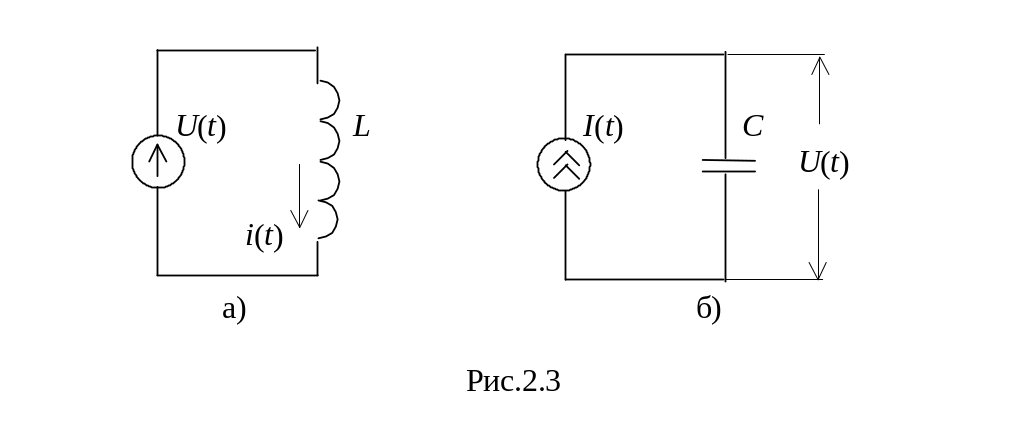
Прикладами диференційних ланок є підключення індуктивності L (рис.2.3,а) до джерела напруги U(t) та підключення конденсатора С (рис.2.3,б) до джерела струму I(t) . Динамічні процеси в ланці рис.2.3,а характеризуються рівнянням

, (2.5)

а в ланці рис.2.3,б – рівнянням

. (2.6)

2.1.4. Аперіодична ланка.

Динамічні процеси в аперіодичній ланці описуються диференційним рівнянням

. (2.7)

Замінивши в рівняння (2.7) операцію диференціювання на інтегрування і записавши одержаний результат відносно вихідного сигналу y(t) одержуємо

. (2.8)

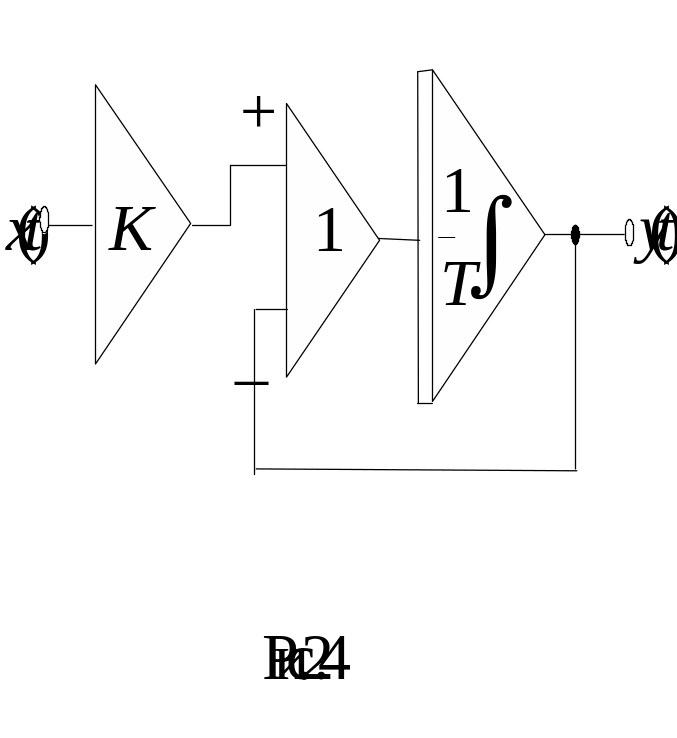
Виразу (2.8) відповідає модель (рис.2.4) аперіодичної ланки.

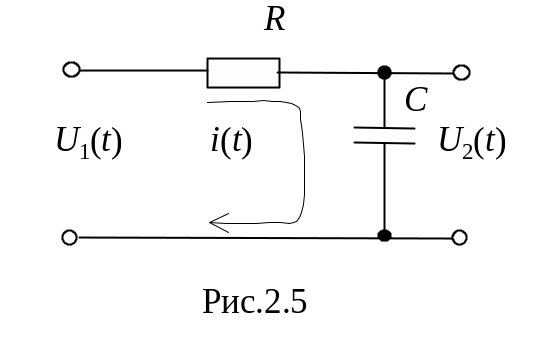Прикладом аперіодичної ланки є електрична схема RC -ланки, що показана на рис.2.5. Динамічні процеси в такій ланці описуються наступною системою диференційних рівнянь

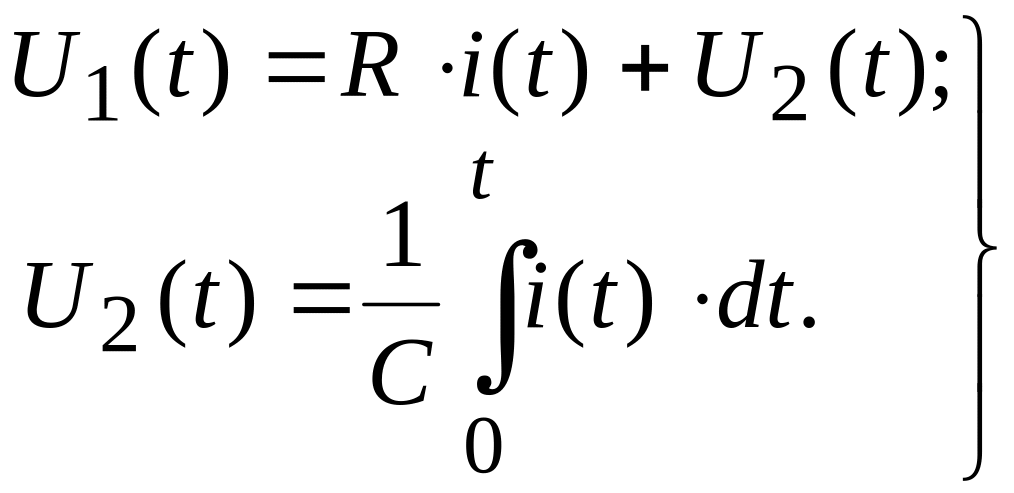(2.9)

Розв'язавши систему рівнянь (2.9), одержуємо

, (2.10)

де RC=T- стала часу аперіодичної ланки.

Одержане рівняння (2.10) структурно співпадає із рівнянням (2.7) при К=1.

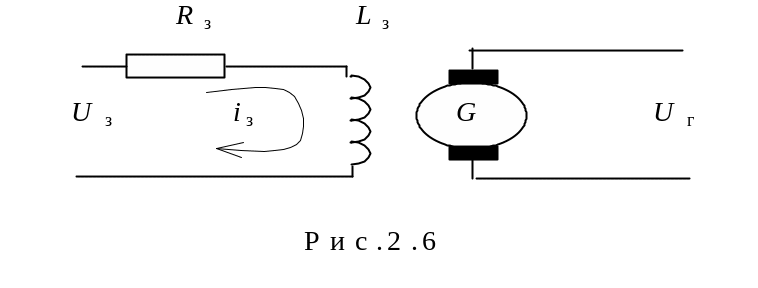Другим прикладом аперіодичної ланки є генератор постійного струму. Генератор являє собою підсилювач в якому зміною струму збудження i_з(t) відбувається керування струму i_я(t) кола якоря. На схемі рис.2.6 R_з і L_з– активний опір та індуктивність кола збудження.

При постійних обертах якоря динамічні процеси в генераторі визначаються системою рівнянь

(2.11)

де - коефіцієнт підсилення по напрузі від кола збудження до якірного кола.

Виключивши струм із системи рівнянь (2.11), одержимо диференційне рівняння

, (2.12)

де - електромагнітна стала часу кола збудження генератора.