1.5. Типові діяння в системах автоматичного регулювання. Основні задачі теорії автоматичного керування

Системи автоматичного регулювання працюють в двох основних режимах: усталеному і неусталеному. Неусталений режим часто називають перехідним або динамічним. Він викликається зовнішніми збуреннями або зміною параметрів системи автоматичного регулювання. Під параметрами системи розуміють слідуючи показники регулятора і об'єкта регулювання: постійні часу, коефіцієнти передачі (підсилення), величини ємності конденсатора, величини індуктивностей дроселів, величини опорів резисторів електричних кіл.

Зовнішні діяння (збурення), що діють на систему регулювання, представляють функцію закон зміни якої в часі важко передбачити. Тому при дослідженні динамічних режимів систем автоматичного регулювання застосовують типові закони змін зовнішніх діянь:

• одинична ступенева функція . Аналітично ступенева функція описується наступним чином

(1.27)

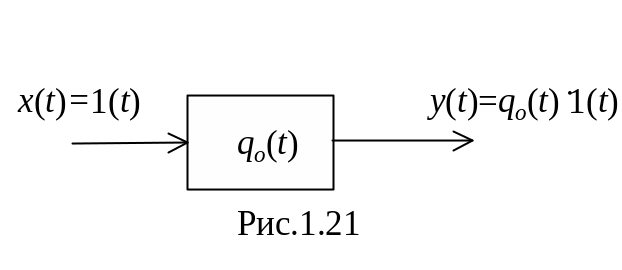
Графік даної функції приведено на рис.1.20. Дана функція моделює, наприклад, ступінчате збільшення або зменшення навантаження. Дана функція також може моделювати ступінчату зміну вхідного діяння (див. рис.1.21) при дослідження динамічних властивостей системи автоматичного регулювання.

• лінійно зростаюча функція (рис.1.22)

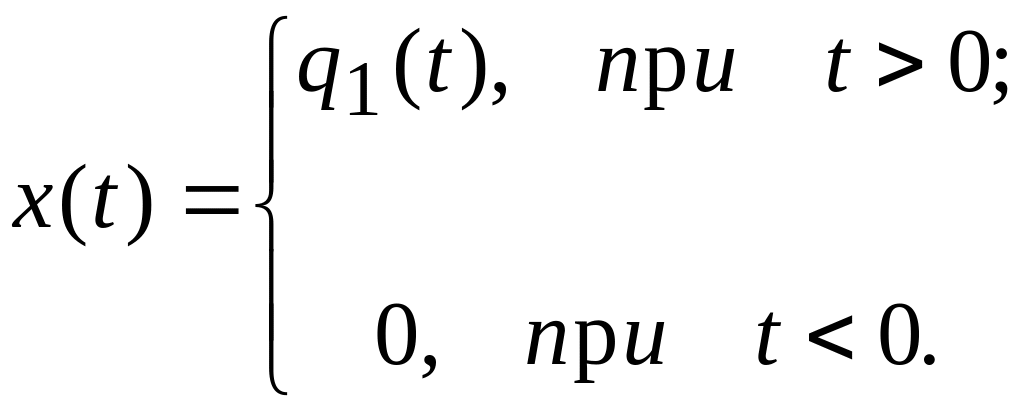
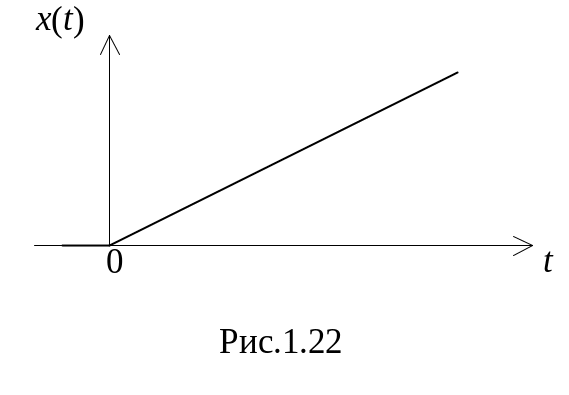(1.28)

Дана функція, наприклад, моделює вхідне діянні слідкуючої системи автоматичного регулювання. Вихідний сигнал система регулювання згідно із рис.1.21 визначається як

. (1.29)

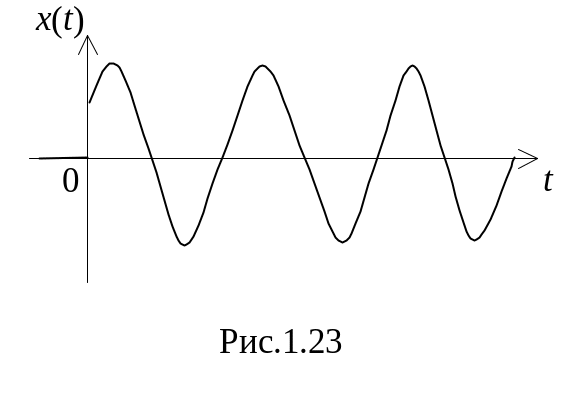
• гармонійне діяння (рис.1.23)

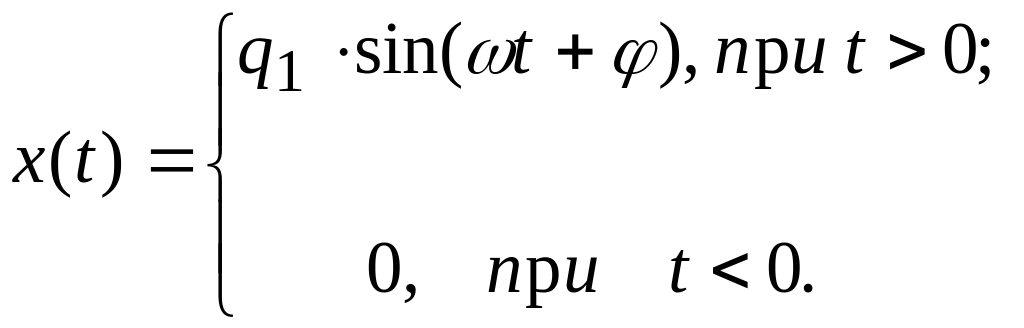(1.30)

Даний сигнал застосовується для моделювання, наприклад, дію вібрації або качки на об'єкт регулювання.

• дельта функція (рис.1.24)

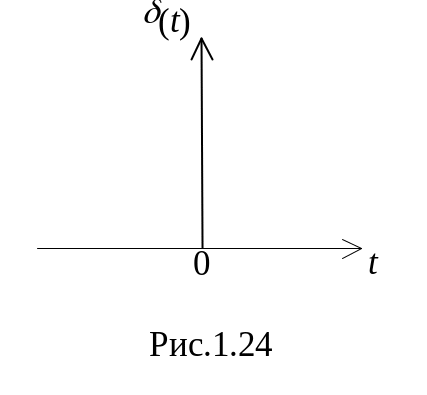
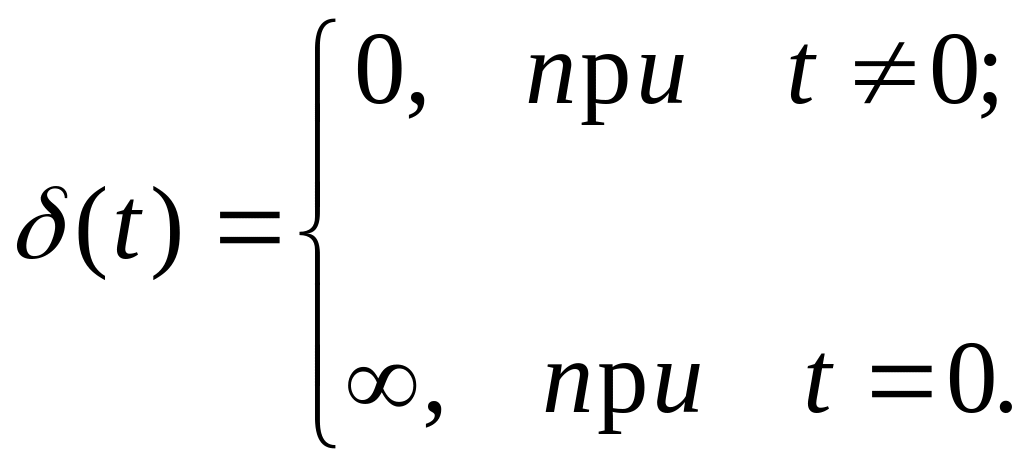(1.31)

Дельта функція представляє собою математичну ідеалізацію імпульсу безконечно малої тривалості площа якого дорівнює одиниці

(1.32)

Дана функція застосовується для моделювання, наприклад, дії імпульсної завади.

Яким би не було зовнішнє діяння, воно завжди викликає в системі автоматичного регулювання перехідний процес. Якщо цей процес в часі затухає, то після його закінчення система приходить в усталений стан. При цьому початкові відхилення його вихідної координати зменшуються до нуля. Такі системи називають стійкими. В стійких системах перехідний процес з часом затухає. Якщо перехідний процес не затухає, то система не стійка. Поведінка стійкої системи автоматичного регулювання в перехідному режимі характеризує її якість. В загальному випадку вихідна величина такої системи складається з двох складових

, (1.33)

де: у_y(t) – усталена складова ; у_п(t) – перехідна складова.

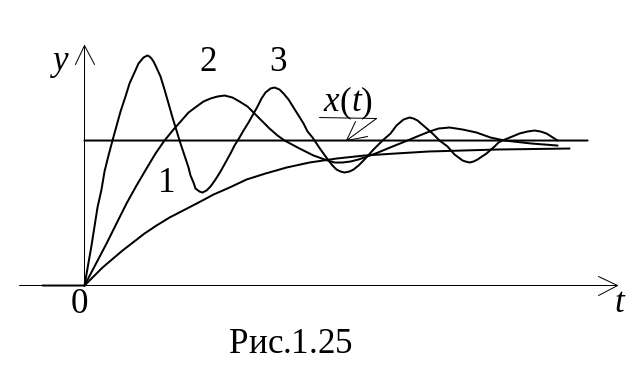Характер змін перехідної складової залежить від властивостей системи автоматичного регулювання. У достатньо сильно демпфіруваних системах перехідна складова змінюється по експоненті – крива 1 на рис.1.25. У слабо демпфірованих системах перехідна складова має коливальний характер – криві 2,3 на рис.1.25.

Основними задачами теорії автоматичного регулювання є:

аналіз – дослідження відомої системи автоматичного регулювання з метою визначення її властивостей та шляхів поліпшення;

синтез – проектування системи автоматичного регулювання, що відповідає заданим вимогам.

Основними етапами синтезу є:

1. Вивчення об'єкта регулювання, умов його роботи і основних збурю-

ючих діянь.

2. Формування вимог, що пред'являються до системи автоматичного регулювання.

3. Вибір принципу регулювання та первісної схеми регулятора.

4. Вибір елементів регулятора.

5. Розрахунки елементів регулятора на основі вимог в статичному і динамічному режимах.

6. Теоретичні дослідження статичного та динамічного режимів.

7. Експериментальні дослідження та корегування системи автоматичного регулювання.

8. Виготовлення та монтаж системи автоматичного регулювання.

9. Наладка системи автоматичного регулювання в реальних умовах роботи.

10. Дослідна експлуатація.

При проектуванні системи автоматичного регулювання використовують як теоретичні, так і експериментальні моделі. Застосування теоретичних методів аналізу і синтезу вимагає попереднього опису системи автоматичного регулювання. Систему рівнянь, що описують роботу системи автоматичного регулювання називають її математичною моделлю. В залежності від характеру математичної моделі системи автоматичного регулювання розрізняють як лінійні і нелінійні. Лінійна системи автоматичного регулювання – система яку із достатньо високим ступенем точності можна описати лінійними диференційними рівняннями. Нелінійна система описується нелінійними диференційними рівняннями.

В усталеному режимі властивості системи визначаються статичною ха-

рактеристикою. Статичною характеристикою системи (елемента) називається залежність між вхідною та вихідною величинами. Статичні характеристики елементів, на базі яких одержують статичну характеристику системи, розраховують, або одержують експериментально. Приклади статичних характеристик елементів наведені на рис.1.26.

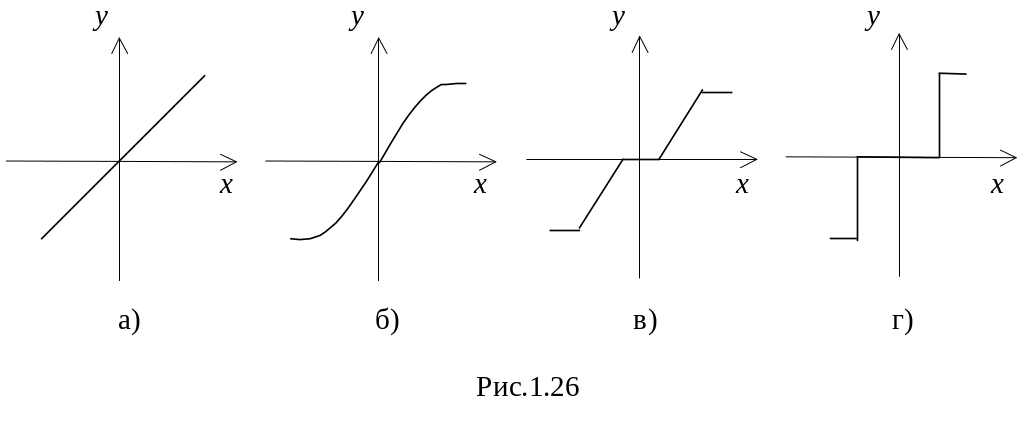Статична характеристика на рис.1.26,а є лінійною, на рис.1.26,б – нелінійна, а на рис.1.26,в,г – суттєво нелінійні.