1.10.2. Некоторые важные примеры приложений.
Пример 4.1. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка вида
(4.31)
где
;
,
(4.32)
причем
– искомые функции;
– заданные функции;
– матрица, не зависящая от x.
Общее решение задачи (4.31) определяется формулой:
.
(4.32)
Пример 4.2. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка вида
(4.33)
Пусть
– положительно определенная матрица,
т.е. все ее собственные числа
.
Тогда общее решение (4.33) можно записать
в виде:
.
(4.34)
Пример 4.3. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка вида
(4.35)
Общее решение задачи (4.35) определяется формулой:
,
(4.36)
где
и
– гиперболические синус и косинус от
произвольного аргумента.
1.10.3. Дискретно-аналитический метод решения задачи теплопроводности
Математическая постановка задачи имеет вид:
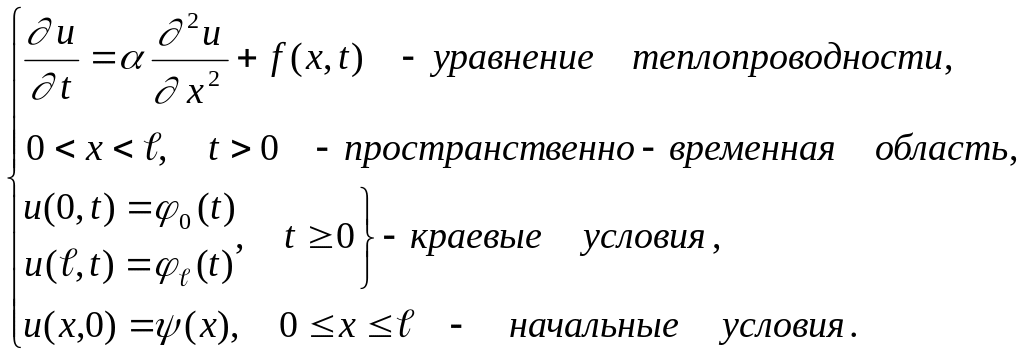(4.37)
где
– координата по
толщине стены,
;
– координата по времени,
;
– значение температуры в точке
во время
;
– коэффициент температуропроводности
материала;
– функция, характеризующая мощность
возможного источника тепла.
Задача (4.37) определена в пространственно-временной области W:
.
(4.38)
Отметим, что
;
.
(4.39)
Заметим, что поскольку задача (4.37) содержит начальные условия по времени, то она является задачей Коши.
Ниже рассмотрим дискретно-аналитический метод решения задачи, который состоит в следующем: по оси x осуществляется конечно-разностная аппроксимация, а по времени t рассматривается непрерывная (континуальная) задача.
Пусть
,
– координаты точек разбиения, причем
и
– граничные точки (в которых заданы
краевые условия). Таким образом, искомыми
будут являться функции
,
во внутренних узлах сетки. Схема
аппроксимации пространственно-временной
области в данном случае условно показана
на рис. 5.5.1.
Рис. 4.1. Пространственно-временная область:
Во всех внутренних точках узлах уравнение теплопроводности в (4.37) примет вид:
(4.40)
при этом пусть
,
.
(4.41)
В соответствии с краевыми условиями из (4.37) для граничных точек, в свою очередь, можем записать:
,
,
.
(4.42)
Следовательно,
уравнения теплопроводности для узлов
с номерами
и
имеют соответственно вид:
;
(4.43)
.
(4.44)
Введем обозначения:
;
,
(4.45)
где
;
.
(4.46)
Получаем матричную формулировку разрешающей системы уравнений:
(4.47)
где
;
;
.
(4.48)
Согласно (4.31)-(4.32) общее решение задачи (4.47) имеет вид:
.
(4.49)
Если
не зависит от
,
переходим к формуле
.
Выполняем интегрирование:
,
откуда
.
(4.50)
Реализация формулы
(4.50)
предполагает вычисление экспоненты от
матрицы
,
для выполнения которого следует
воспользоваться результатами предыдущего
параграфа (см. формулу (4.17)). Имеем:
,
(4.51)
где
– матрица собственных векторов матрицы ;
– обратная матрица к матрице ;
;
(4.52)
– собственные
числа матрицы
,
.
Аналогично можем вычислить
,
где
.
(4.53)
Варианты задания.
– функция,
характеризующая мощность источника
тепла;
– коэффициент
температуропроводности материала
стены;
– краевые
условия;
– начальные
условия;
– толщина стены;
– номер группы,
– номер студента по журналу.
Текст М-файла
function teplo_1_expm
s=input('s=');
g=input('g=');
n=input('n=');
l=input('l=');
alpha=input('alpha=');
h=l/n;
c=alpha/h^2;
m=n-1; a1=ones(m-1,1);
A=diag(a1,-1)-2*eye(m)+diag(a1,1),A=c*A;
u0=g; ul=s;
F=c*[u0;zeros(m-2,1);ul];
xi=(0:h:l)';x=xi(2:n);
U0=g+(g+3*s)*x-2*(g+s)*x.^2;
t=[0 0.15 1.5];
nt=length(t);res=zeros(nt,n+1);
fprintf('\n значения функции температуры U(x,t)\n')
for i=1:nt
res(i,:)=[u0 ut(t(i),F,U0,A)' ul];
fprintf('U(%4.2f):',t(i)),fprintf('%6.2f',res(i,:)),fprintf('\n')
end
hold on
plot(xi,res(1,:),'.-')
plot(xi,res(2,:),'o-.r')
plot(xi,res(nt,:),'*:g')
grid on
s1=sprintf('t=%2.0f',t(1));
s2=sprintf('t=%4.2f',t(2));
s3=sprintf('t=%4.2f',t(nt));
legend(s1,s2,s3,0)
title(sprintf('U(x,t)=exp(At)*U0-inv(A)*(E-exp(At))*F\n%s %s %s', s1,s2,s3))
function U=ut(t,F,U0,A)
m=size(A);E=eye(m);
eAt=expm(t*A);
U=eAt*U0-A\(E-eAt)*F;
Замечание.
Здесь вычисление функции от матрицы
реализуется с использованием стандартной
функции expm(At),
в которой используется алгоритм
Результаты счета
s=12
g=3
n=8
l=1
alpha=1
A =
-2 1 0 0 0 0 0
1 -2 1 0 0 0 0
0 1 -2 1 0 0 0
0 0 1 -2 1 0 0
0 0 0 1 -2 1 0
0 0 0 0 1 -2 1
0 0 0 0 0 1 -2
значения функции температуры U(x,t)
U(0.00): 3.00 7.41 10.88 13.41 15.00 15.66 15.38 14.16 12.00
U(0.15): 3.00 4.81 6.52 8.03 9.29 10.28 11.02 11.56 12.00
U(1.50): 3.00 4.13 5.25 6.38 7.50 8.63 9.75 10.88 12.00
>>
Дискретно-аналитический метод решения задачи о колебаниях балки при ударе
Математическая формулировка задачи.
Рассматривается задача о действии поперечной ударной нагрузки в середине балки (рис. 4.2), определяется линия прогибов балки для любого момента времени.
Рис. 4.2. Расчетная схема балки.
Математическая формулировка задачи имеет вид:
(4.54)
где
– прогиб балки в точке
в момент времени
;
– координата по длине балки,
;
– координата по времени,
;
;
– изгибная жесткость балки;
– плотность материала балки;
– функция, моделирующая поперечное
ударное воздействие по балке в точке
;
и
– дельта-функции.
Дискретно-аналитический метод решения задачи.
Для решения задачи будем использовать дискретно-аналитический метод, который состоит в следующем: по оси x осуществляется конечно-разностная аппроксимация, а по оси времени t рассматривается непрерывная задача (рис. 4.3).
Рис. 4.3. Схема дискретизации.
Введем обозначения:
;
,
,
(4.55)
где в простейшем случае
.
(4.56)
Здесь
– количество внутренних узлов
конечно-разностной сетки, причем пусть
– нечетное число.
Для всех внутренних
узлов
получим конечно-разностное уравнение
– дискретный аналог уравнения колебаний
(4.54):
,
,
(4.57)
где
(4.58)
– вторая конечная
разность, приближенно представляющая
вторую производную от искомой функции
по аргументу
.
В соответствии с краевыми условиями из (4.54) для граничных узлов, очевидно, можем записать:
;
;
;
.
(4.59)
C учетом (4.59) преобразуются уравнения (4.57) Имеем:
;
(4.60)
;
(4.61)
,
;
(4.62)
;
(4.63)
.
(4.64)
Обоснуем, например, (4.60) и (4.61):
;
Введя обозначение
,
(4.65)
можем представить разрешающую систему конечно-разностных уравнений (4.60)-(4.64) в матричном виде
(4.66)
где
.
(4.67)
Заметим, что матрица положительно определена, т.е. все ее собственные числа положительные (в этом можно убедиться при их непосредственном вычислении).
Общее решение задачи (4.66) имеет вид:
.
(4.68)
По условию рассматриваемой задачи
, (4.69)
откуда следует, что
,
где
.
(4.70)
Это значит, что в
векторе
лишь один «срединный элемент» (с номером
)
равен единице, а остальные элементы
равны нулю. Ненулевой элемент вектора
соответствует узлу конечно-разностной
сетки с координатой
,
в котором
в момент времени
приложено
сосредоточенное ударное воздействие
величиной
.
Подставив (4.69) в (4.68), получим окончательный вид общего решения:
.
(4.71)
Варианты задания.
– величина
приложенного сосредоточенного ударного
воздействия;
;
;
– номер группы,
– номер студента по журналу.
Принять
количество количество внутренних узлов
конечно-разностной сетки
.
Пример соответствующего M-файла (ниже задано , ):
function blow_f
g=input('g=');
s=input('s=');
n=input('n=');
L=300;P=300;
h=L/(n+1);
alfa=10^8*(100+g+s);
x=0:h:L;
a0=6*eye(n);a0(1,1)=5;a0(n,n)=5;
a1=ones(n-1,1);
a2=ones(n-2,1);
A=a0-4*(diag(a1,-1)+diag(a1,1))+diag(a2,-2)+diag(a2,2)
A=alfa*A/h^4;
F=zeros(n,1);F((n+1)/2)=P;
sq_A=sqrtm(A);
fJ=sqrt(eig(A));
t0=pi/(4*fJ(n));
tmax=125*t0;
nt=3;
t=[t0,tmax/2,tmax];
res=zeros(nt,n+2);
fprintf('\n прогиб балки Y(x,t)\n')
for i=1:nt
Y_t=inv(sq_A)*funm(sq_A*t(i),'sin')*F;
res(i,2:n+1)=Y_t';
fprintf('Y(%6.4f):',t(i)),fprintf('%8.4f',res(i,:)),fprintf('\n')
end
hold on
plot(x,res(1,:),'.-')
plot(x,res((nt+1)/2,:),'o-.r')
plot(x,res(nt,:),'*:g')
grid on
s1=sprintf('t=%6.4f',t(1));
s2=sprintf('t=%6.4f',t((nt+1)/2));
s3=sprintf('t=%6.4f',t(nt));
legend(s1,s2,s3,0)
title(sprintf('Y(x,t)=-inv(sqrt(A))*sin(sqrt(A)t))*F\n%s %s %s', s1,s2,s3))
Результаты расчета:
g=3
s=12
n=7
A =
5 -4 1 0 0 0 0
-4 6 -4 1 0 0 0
1 -4 6 -4 1 0 0
0 1 -4 6 -4 1 0
0 0 1 -4 6 -4 1
0 0 0 1 -4 6 -4
0 0 0 0 1 -4 5
прогиб балки Y(x,t)
Y(0.0027): 0.0000 -0.0001 -0.0053 0.0217 0.7703 0.0217 -0.0053 -0.0001 0.0000
Y(0.1673): 0.0000 2.2085 4.2797 5.8565 5.5146 5.8565 4.2797 2.2085 0.0000
Y(0.3346): 0.0000 -1.3399 -3.5149 -3.9787 -4.1294 -3.9787 -3.5149 -1.3399 0.0000
>>
Замечание. Здесь вычисление функций от матрицы A реализуются следующим образом:
с использованием
стандартной функции sqrtm(A),
с использованием
funm(sqrtm(A),’sin’).
Function |
Syntax for Evaluating Function at Matrix A |
exp |
funm (A, @exp) |
log |
funm(A, @log) |
sin |
funm(A, @sin) |
cos |
funm(A, @cos) |
sinh |
funm(A, @sinh) |
cosh |
funm(A, @cosh) |
Кроме
того, для вычисления
,
и
можно использовать встроенные функции
expm(A),
logm(A)
и sqrtm(A),
соответственно.