
Зміст
Границя функції. Означення по Гейне і Коші _____________________2
Границя функції в точці_______________________________________3
Односторонні границі_________________________________________5
Неперервність функції на множині______________________________7
Точки розриву_______________________________________________8
Властивості неперервних функцій_______________________________9
Правила границь функції______________________________________11
Границя функції двох змінних_________________________________12
Список ілюстрацій___________________________________________15
Границя функції. Означення по Гейне і Коші
Нехай
![]() ,
де X,
F
– топологічні простори, а
,
де X,
F
– топологічні простори, а
![]() і точка
і точка
![]() – гранична для А.
– гранична для А.
Означення
1 (топологічне). Точка
![]() – границя функції
– границя функції
![]() при
при
![]() по множині А,
якщо для будь-якого околу V
точки
по множині А,
якщо для будь-якого околу V
точки
![]() в F
існує окіл U
точки
в X
такий, що
в F
існує окіл U
точки
в X
такий, що
![]() .
Позначаємо:
.
Позначаємо:
![]() .
.
Приклад.
1) Х=R,
A=N,
![]() ,
,
![]() –
отримуємо
границю послідовності.
–
отримуємо
границю послідовності.
2)
![]() .
.
Нехай Х – метризований простір, тоді означення буде еквівалентне означенню функції по Гейне.
Означення
2. Точка
– границя функції
при
по множині А
(
– гранична точка А)
якщо для будь-якої послідовності
![]() ,
то
,
то
![]() в F.
в F.
Доведемо еквівалентність означень.
Означення
2 випливає з означення 1 (навіть якщо Х
просто топологічна множина). Дійсно,
нехай означення 1 виконується. Якщо
![]() ,
то
,
то
![]() ,
тобто
,
тобто
![]() .
.
Доведемо,
що означення 1 випливає з означення 2.
Нехай виконується означення 2. Припустимо,
що означення 1 не виконується, тобто
![]() .
Візьмемо за U
пари
.
Візьмемо за U
пари
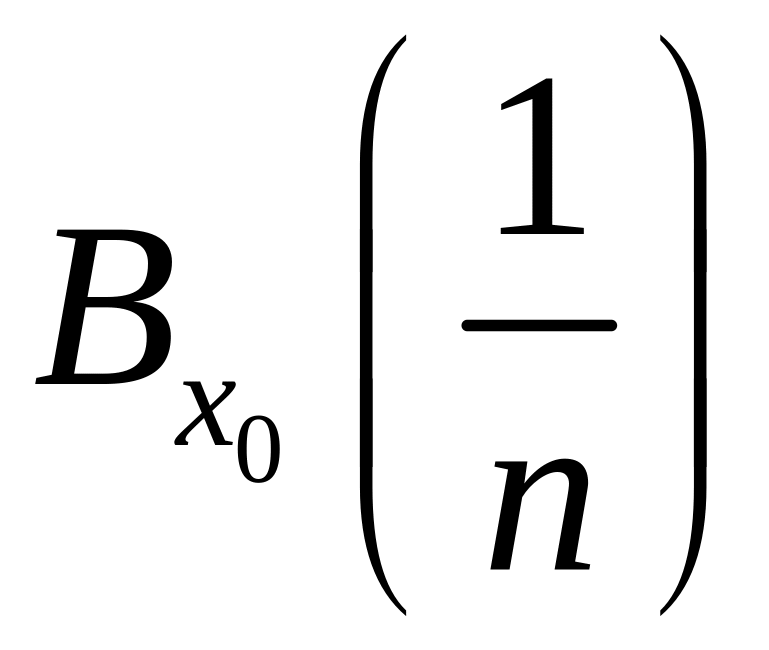 ,
тоді
,
тоді
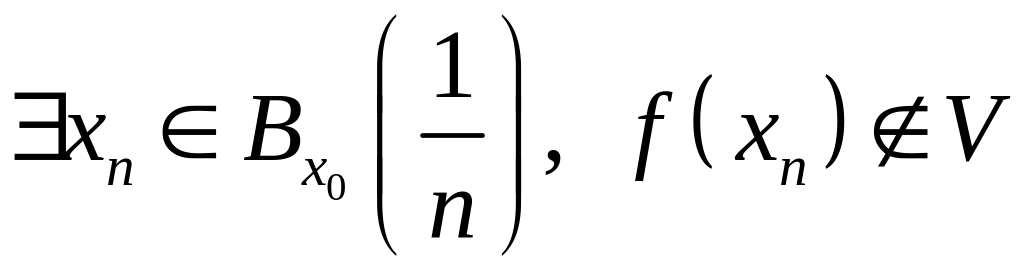 (перетин не порожній, так як точка
гранична). Одержали суперечність:
(перетин не порожній, так як точка
гранична). Одержали суперечність:
![]() ,
яка і доводить твердження.
,
яка і доводить твердження.
Розглянемо
ситуацію, коли Х
і F
– метричні простори з метриками
![]() і
і
![]() відповідно.
відповідно.
Означення
(по
Коші) . Точка
називається границею
при
по А,
якщо
![]() .
.
Означення по Коші та по Гейне еквівалентні.
Границя функції в точці
Рисунок 1
Нехай
функція
![]() визначена
на деякій множині X і точкаxn
визначена
на деякій множині X і точкаxn
![]() .
Візьмемо з X послідовність точок
.
Візьмемо з X послідовність точок
![]() ,
відмінних від a, яка збігається до цього
числа:
,
відмінних від a, яка збігається до цього
числа:
x1, x2, x3,….,xn,….. (1)
Значення
функції
в точках послідовності (1) утворюють в
свою чергу числову послідовність
![]() :
:
f(x1), f(x2), f(x3),…,f(xn),…. (2)
Означення
1. (за Гейне). Число b називається границею
функції (limit of function) f(x)
в точці x=a
(або при
![]() ), якщо для будь-якої збіжної до a
послідовності (1) значень аргументу x,
відмінних від a, відповідна послідовність
(2) значень функції збігається до числа
b.
), якщо для будь-якої збіжної до a
послідовності (1) значень аргументу x,
відмінних від a, відповідна послідовність
(2) значень функції збігається до числа
b.
Позначають це так:
![]() f(x)
=b
(3)
f(x)
=b
(3)
або
f(x)![]() b
при x
a.
b
при x
a.
Це означення границі функції за Гейне (мовою послідовностей), його можна записати скорочено так:
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() f(xn)
=b
f(xn)
=b
Приклад
1.
Довести, що
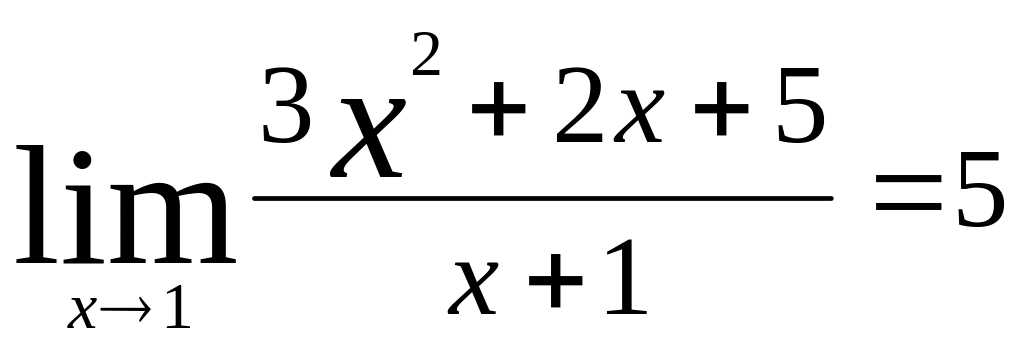 .
.
Доведення.
За означенням 2:
,
![]() ,
lim xn=1;
,
lim xn=1;

Ця границя не залежить від вибору послідовності , яка збігається до числа 1.
Означення 3.
(за Коші). Число b
називається границею функції f(x)
в точці x=a
(або при
),
якщо для будь-якого як завгодно малого
числа
![]() існує таке додатне число
існує таке додатне число
![]() , що для всіх
, що для всіх
![]() , які задовольняють нерівність
, які задовольняють нерівність
![]() , виконується нерівність
, виконується нерівність
![]()
Скорочено це означення можна записати так:
![]()
![]()
![]()
З геометричної точки зору, якщо число b є границею функції в точці , то для всіх значень аргументу , які групуються навколо точки , відповідні значення функції групуються навколо точки .
Зауваження. Можна показати, що означення 2 та 3 є еквівалентними.
Приклад 2. Довести,
що
![]() .
.
Доведення. Застосуємо означення 3:
![]()
![]() (мал1)
(мал1)
![]() ,
тобто
,
тобто
![]() .
.
Нехай, наприклад,
![]() ,
тоді відповідне
,
тоді відповідне
![]() і
і
![]()
![]()
Односторонні границі
Означення
4. Число b
називається границею функції f(x)
справа (right-handed
limit)
[зліва (left-handed
limit)]
в точці x=a,
якщо для будь-якого як завгодно малого
числа
![]() існує таке додатне число
, що для всіх x,
які задовольняють нерівність
існує таке додатне число
, що для всіх x,
які задовольняють нерівність
![]() [
[![]() ],
виконується нерівність
],
виконується нерівність
Скорочено означення границі справа (зліва) в точці , можна записати так:
![]() (
)
(
)![]()
Позначають границю
справа
![]() або f(a+0);
або f(a+0);
границю зліва
![]() або f(a-0).
або f(a-0).
Для існування границі функції f(x) в точці x=a необхідно і достатньо, щоб мала місце рівність
= =b
Побудова
графіків найпростіших функцій, наприклад,
![]() ,
,
![]() або
або
![]() здійснюється за точками. Зокрема
складають таблицю значень функції, що
відповідають певним значенням аргументу,
потім на площині, в якій задана система
координат, будують точки, координати
яких занесено в таблицю; з’єднавши
відмічені точки “суцільною лінією”,
дістають графік функцій. Це можна робити
не завжди, а лише тоді, коли функція
неперервна (тоді графік її є лінія
суцільна).
здійснюється за точками. Зокрема
складають таблицю значень функції, що
відповідають певним значенням аргументу,
потім на площині, в якій задана система
координат, будують точки, координати
яких занесено в таблицю; з’єднавши
відмічені точки “суцільною лінією”,
дістають графік функцій. Це можна робити
не завжди, а лише тоді, коли функція
неперервна (тоді графік її є лінія
суцільна).
Функція
![]() xÎ(a;
b) називається
перервною в точці x0Î(a;
b), якщо
границя функції
в точці х0
існує і дорівнює значенню функції в цій
точці:
xÎ(a;
b) називається
перервною в точці x0Î(a;
b), якщо
границя функції
в точці х0
існує і дорівнює значенню функції в цій
точці:

За цим означенням неперервність функції f в точці х0 означає здійснимість таких умов:
1) функція f повинна бути визначена в точці х0;
2) для функції f повинна існувати границя в точці х0;
3) границя функції f в точці х0 збігається із значенням функції в цій точці.
Наприклад,
функція f(х)=х2
визначена на всій числовій прямій і
![]() Оскільки f(1)=1,
то значення f(х)=х2
в точці х=1
збігається з границею при х®1,
то, згідно з означенням, функція f
(х)=х2
неперервна в точці х=1.
Оскільки f(1)=1,
то значення f(х)=х2
в точці х=1
збігається з границею при х®1,
то, згідно з означенням, функція f
(х)=х2
неперервна в точці х=1.
Якщо
використати означення лівої і правої
границь функції, то можна дати означення
лівосторонньої і правосторонньої
неперервностей функції, тобто функція
називається неперервною зліва в точці
х0,
якщо
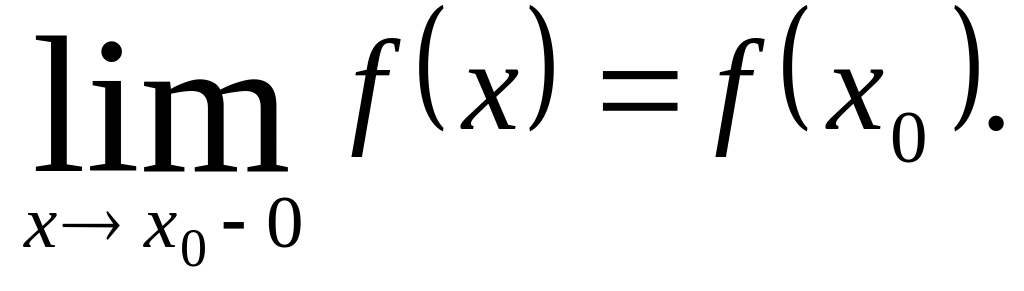 ;
неперервною справа в точці х0,
якщо
;
неперервною справа в точці х0,
якщо
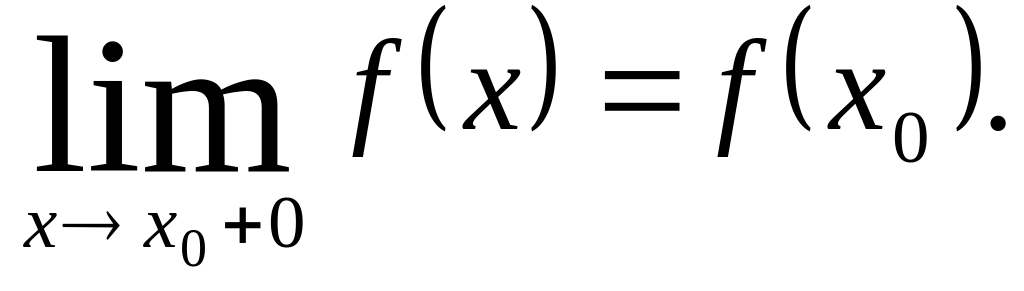
Наприклад,
функція
![]() ,
де
,
де
![]() -
дробова частина числа х, неперервна
всюди, за винятком цілочислових значень
аргументу х, в яких вона неперервна
справа.
-
дробова частина числа х, неперервна
всюди, за винятком цілочислових значень
аргументу х, в яких вона неперервна
справа.
Покажемо дослідження функції на неперервність на конкретних прикладах.
Приклад
1.
Дослідимо на неперервність у точці х0=0
функцію
![]() (читають
“сигнум х” або “знак х”):
(читають
“сигнум х” або “знак х”):
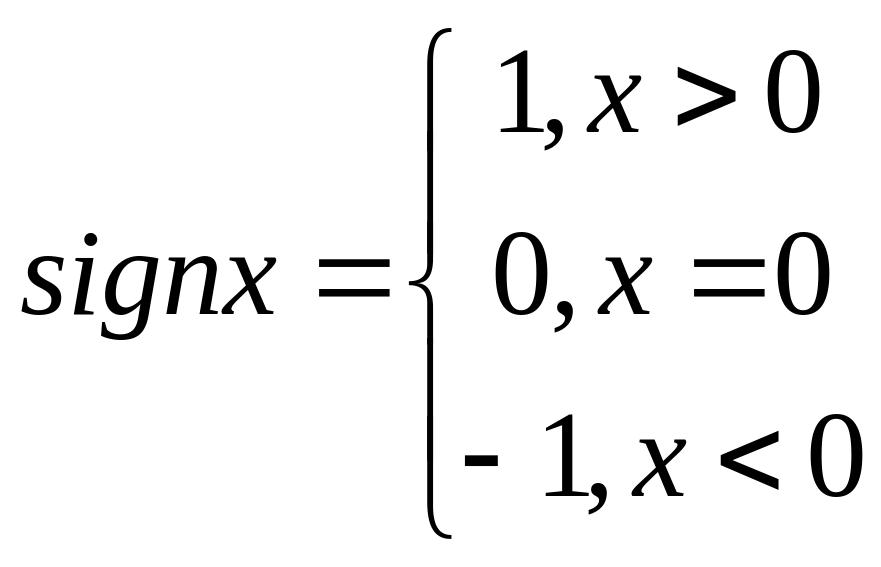
Згідно з заданням функції
![]()
![]()
Таким чином, f(-0)¹f(+0), тобто односторонні границі існують, але різні, тому функція не має границі і, тим більше, не буде неперервною в точці х0=0.
Приклад
2.
Нехай
![]()
Дослідимо
цю функцію на неперервність у точці
х0=0.
Оскільки
![]() для х¹0,
то
для х¹0,
то
![]()
Отже,
границя цієї функції в точці х0=0
існує, але вона не дорівнює
![]() ,
бо
,
бо
![]() ,
і тому функція
не буде неперервною в точці х0=0.
,
і тому функція
не буде неперервною в точці х0=0.
Приклад 3. Нехай дано функцію
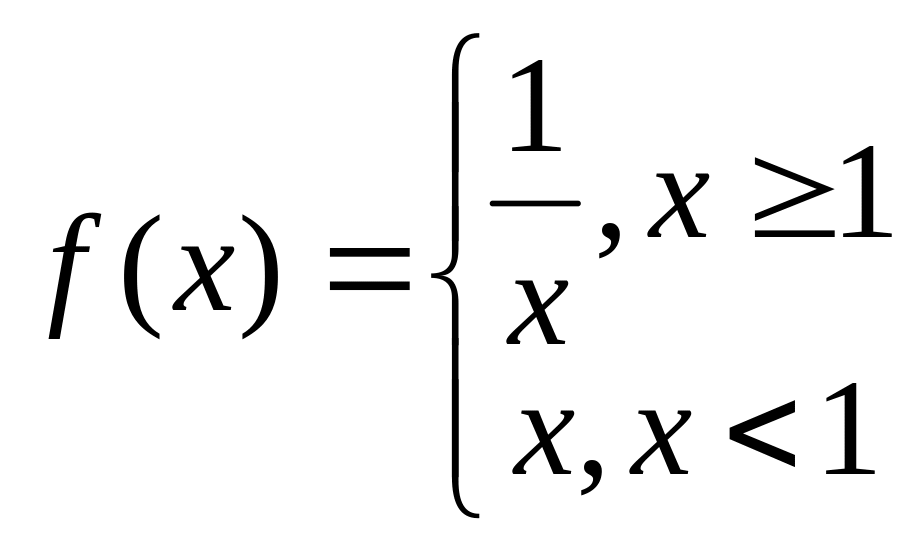
Дослідимо цю функцію на неперервність у точці х0=1.
Оскільки
![]()
![]() ,
то
,
то
![]()
Таким чином, ми встановили, що в точці х0=1 границя функції існує і дорівнює значенню функції, а це означає, що розглянута функція неперервна в точці х0=1.
Приклад
4. Нехай
![]() ,
xÎR,
x¹3
,
xÎR,
x¹3
Ця функція не є неперервною в точці х0=3, бо вона не визначена при х=3.
