
- •Идз № 2 «Числовые и функциональные ряды» Вариант 1
- •Идз № 2 «Числовые и функциональные ряды» Вариант 2
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 3
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 4
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 5
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 6
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 7
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 8
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 9
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 10
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 11
- •7 Вычислить сумму ряда с точностью :. .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 12
- •7 Вычислить сумму ряда с точностью :. .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 13
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 14
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 15
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 16
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 17
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 18
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 19
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 20
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 21
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 22
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.):
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 23
- •7 Вычислить сумму ряда с точностью :. .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 24
- •7 Вычислить сумму ряда с точностью :. .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 25
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 26
- •7 Вычислить сумму ряда с точностью : .
- •8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
- •12 Вычислить интеграл с точностью до 0,001: .
12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 10
Теория (геометрический и обобщенно-гармонический ряды, условия их сходимости и расходимости; необходимое условие сходимости, достаточное условие расходимости числового ряда; первая и вторая теоремы сравнения, признак Даламбера, радикальный и интегральный признаки Коши, признак Лейбница).
Исследовать на сходимость ряды:
1
 . 2
. 2
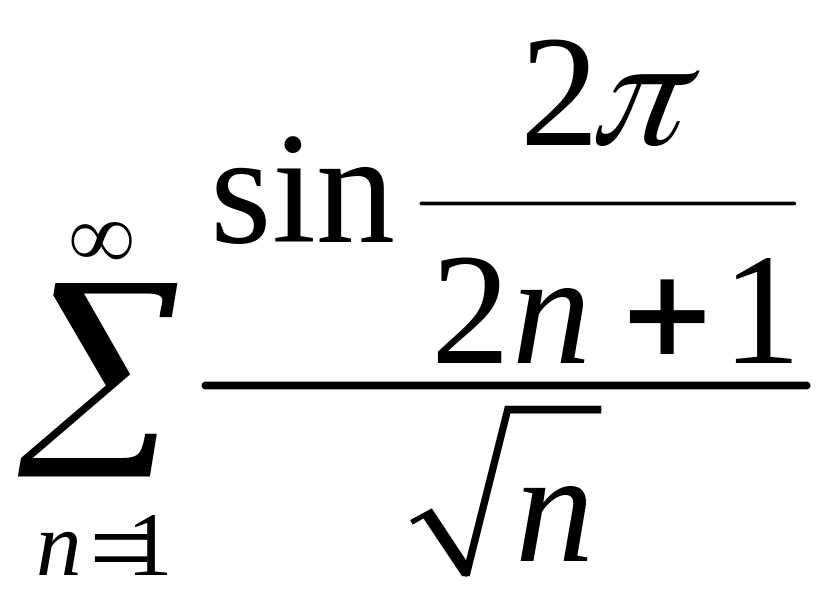 . 3
. 3
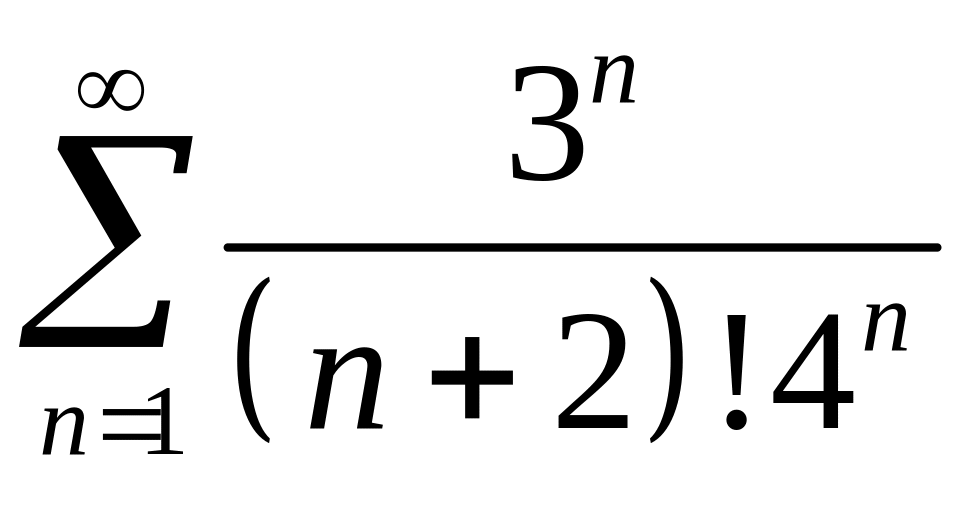 .
.
4
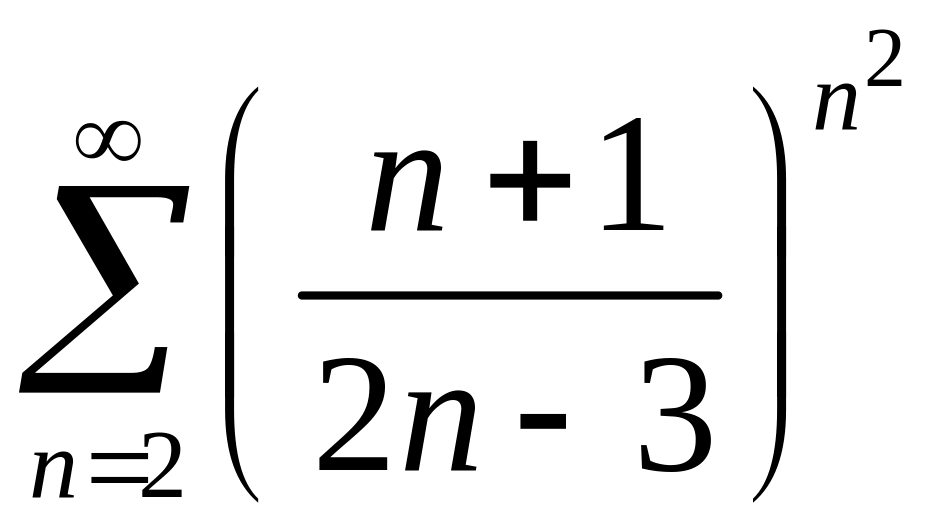 . 5
. 5
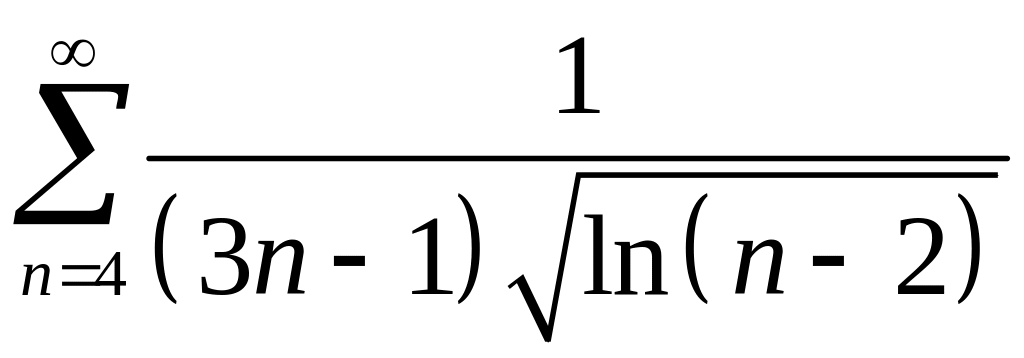 . 6
. 6
 .
.
7 Вычислить сумму ряда с точностью : .
8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
Найти область сходимости функциональных рядов:
9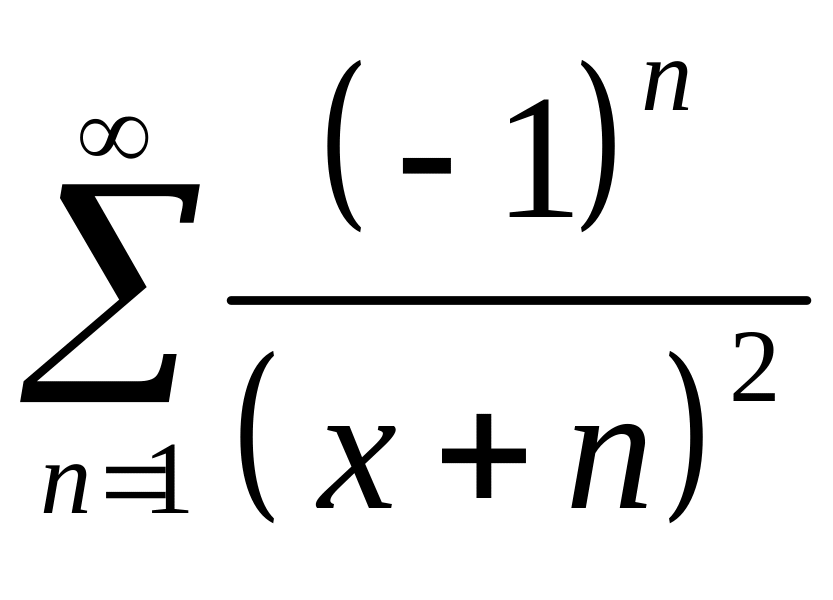 . 10
. 10 . 11
. 11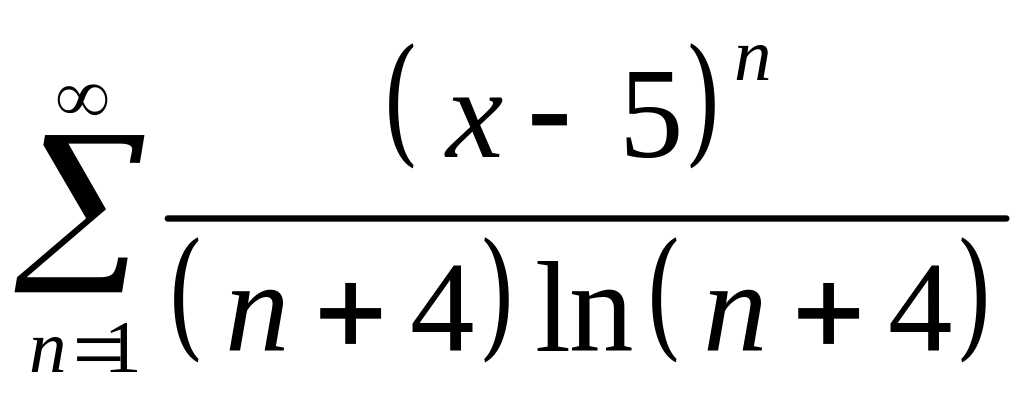 .
.
12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 11
Теория (геометрический и обобщенно-гармонический ряды, условия их сходимости и расходимости; необходимое условие сходимости, достаточное условие расходимости числового ряда; первая и вторая теоремы сравнения, признак Даламбера, радикальный и интегральный признаки Коши, признак Лейбница).
Исследовать на сходимость ряды:
1
 . 2
. 2
 . 3
. 3
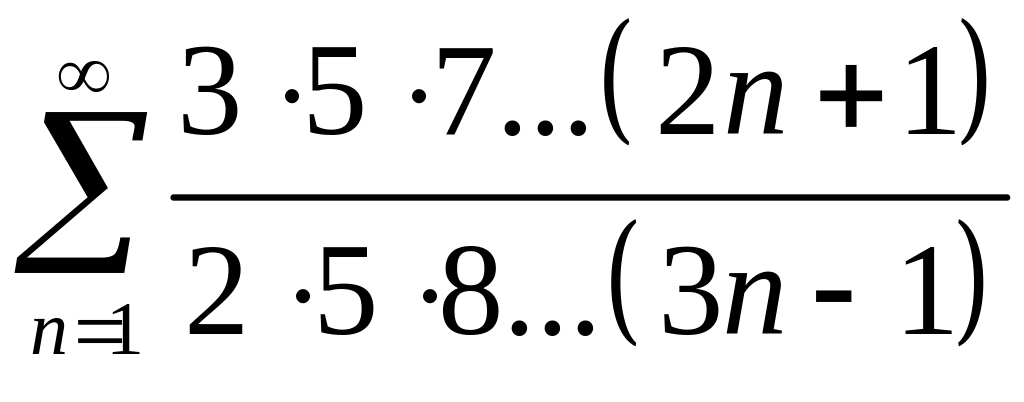 .
.
4
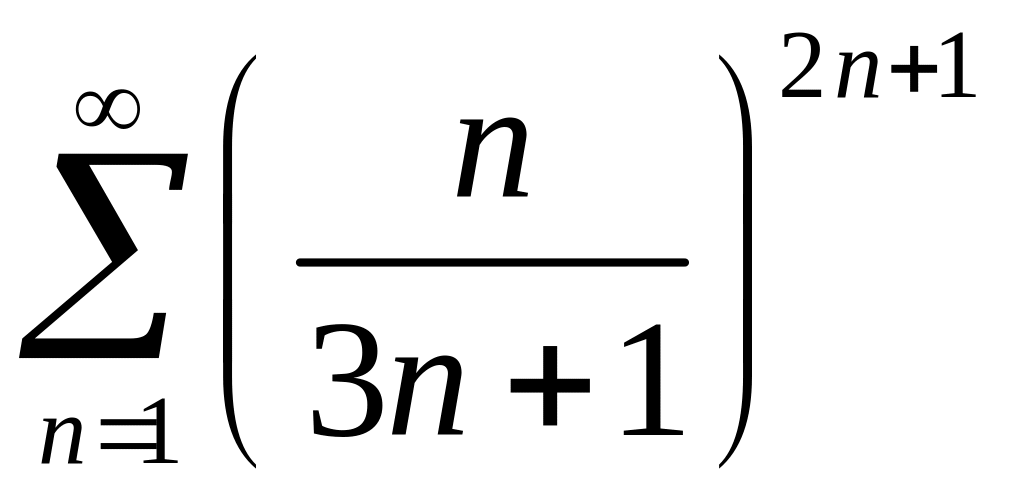 . 5
. 5
 . 6
. 6
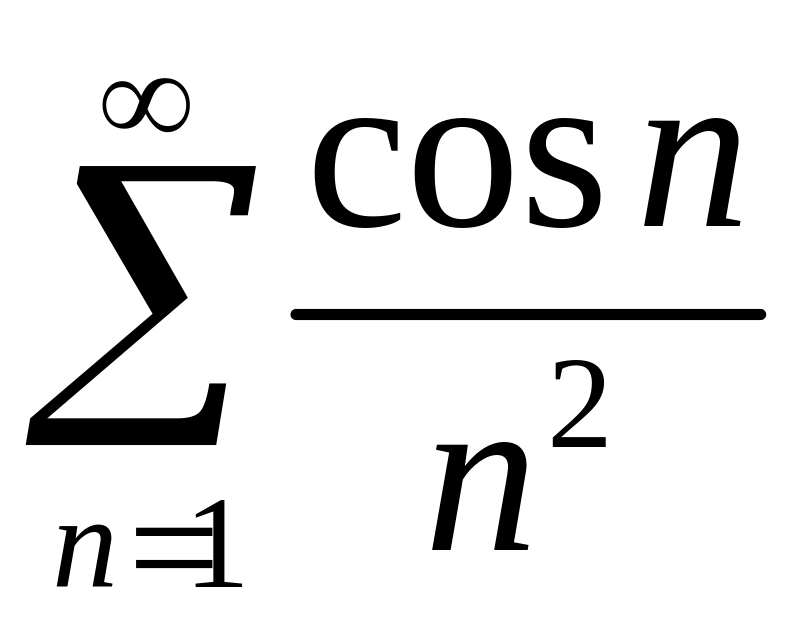 .
.
7 Вычислить сумму ряда с точностью :. .
8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
Найти область сходимости функциональных рядов:
9 . 10
. 10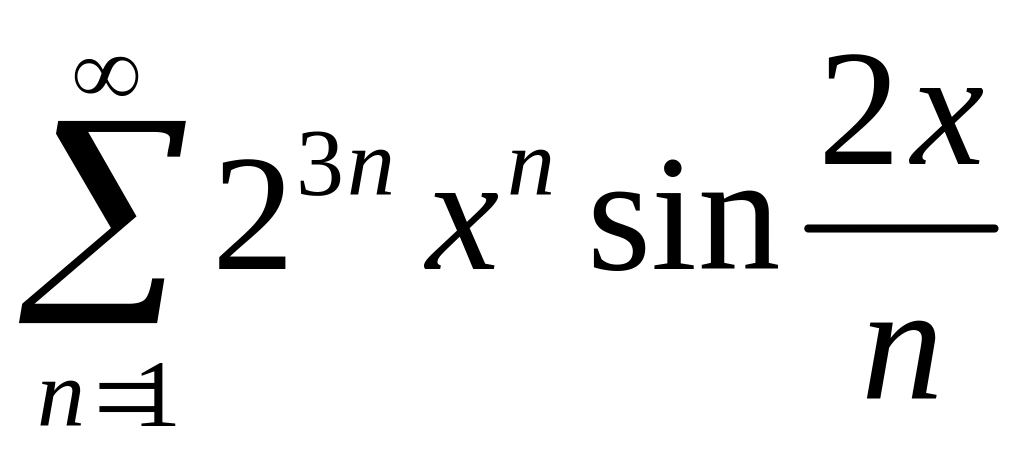 .
.
11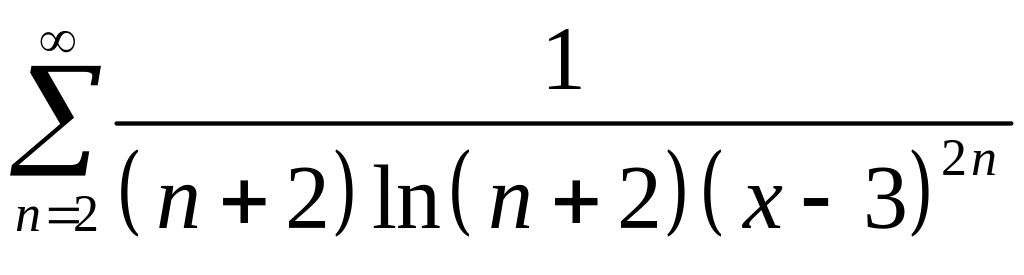 .
.
12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 12
Теория (геометрический и обобщенно-гармонический ряды, условия их сходимости и расходимости; необходимое условие сходимости, достаточное условие расходимости числового ряда; первая и вторая теоремы сравнения, признак Даламбера, радикальный и интегральный признаки Коши, признак Лейбница).
Исследовать на сходимость ряды:
1
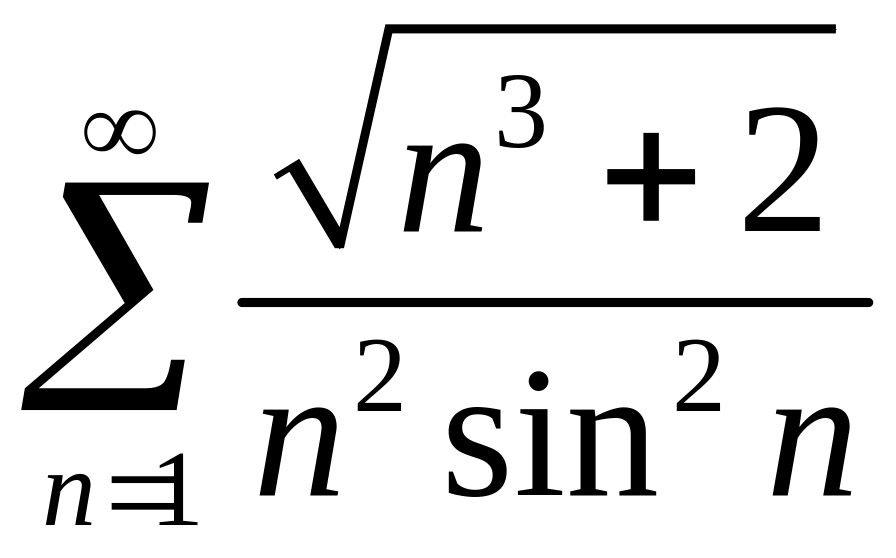 . 2
. 2
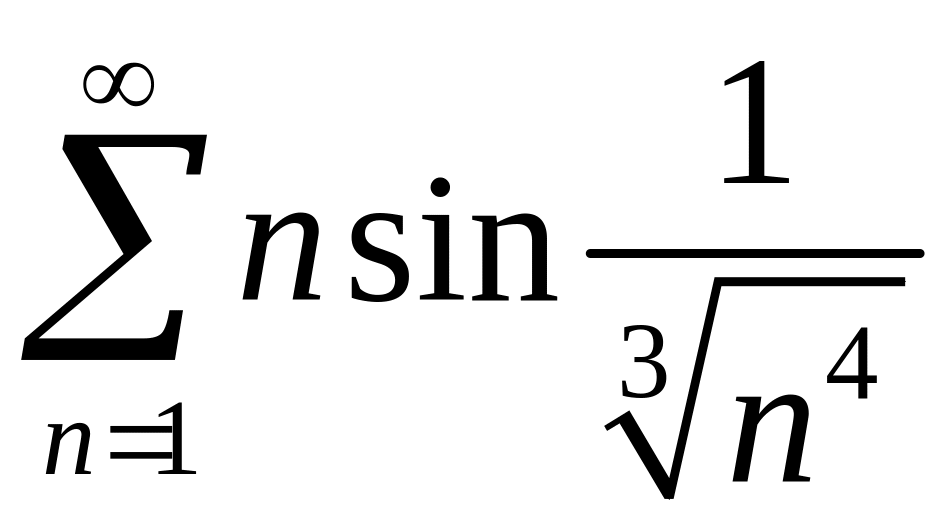 . 3
. 3
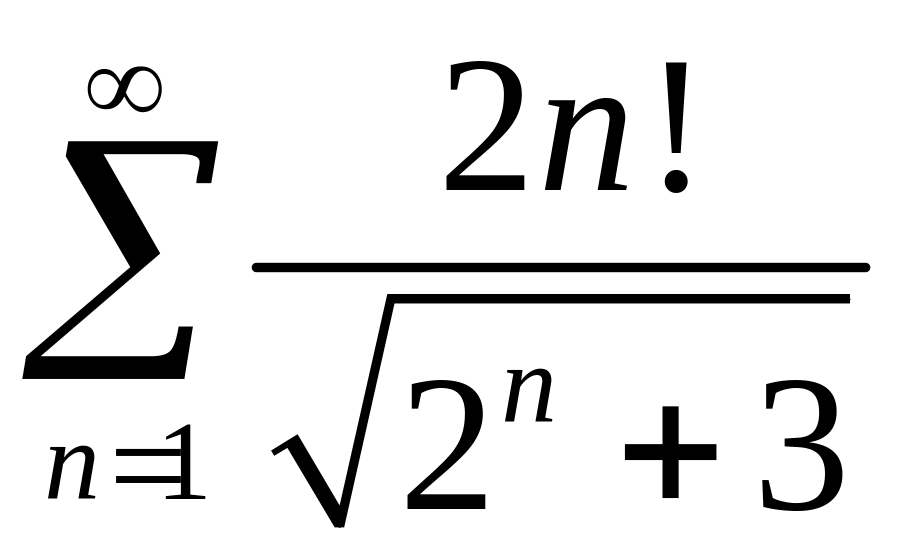 .
.
4
 . 5
. 5
 . 6
. 6
 .
.
7 Вычислить сумму ряда с точностью :. .
8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
Найти область сходимости функциональных рядов:
9 . 10
. 10 . 11
. 11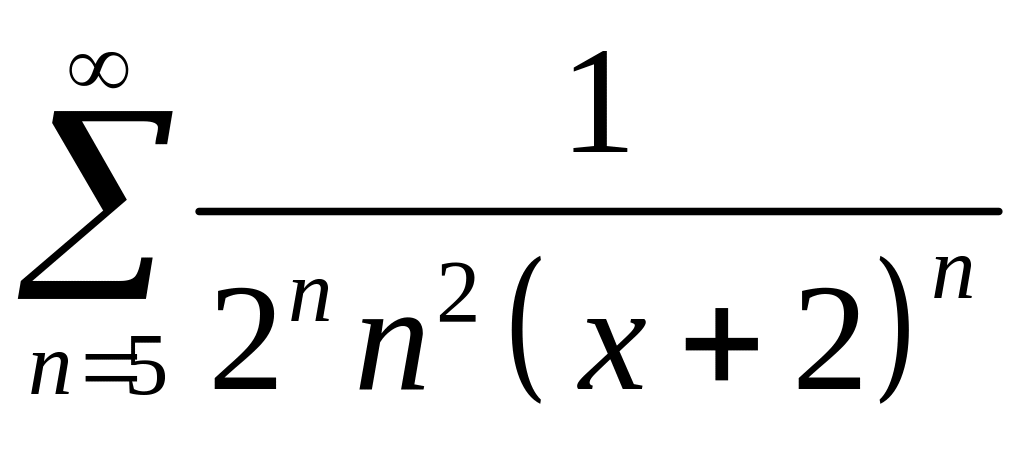 .
.
12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 13
Теория (геометрический и обобщенно-гармонический ряды, условия их сходимости и расходимости; необходимое условие сходимости, достаточное условие расходимости числового ряда; первая и вторая теоремы сравнения, признак Даламбера, радикальный и интегральный признаки Коши, признак Лейбница).
Исследовать на сходимость ряды:
1 . 2 . 3 .
4 . 5 . 6 .
7 Вычислить сумму ряда с точностью : .
8 Доказать справедливость равенства (Ответом служит число , получаемое при применении признака Даламбера или признака Коши.)
Найти область сходимости функциональных рядов:
9 . 10 . 11 .
12 Вычислить интеграл с точностью до 0,001: . Идз № 2 «Числовые и функциональные ряды» Вариант 14
Теория (геометрический и обобщенно-гармонический ряды, условия их сходимости и расходимости; необходимое условие сходимости, достаточное условие расходимости числового ряда; первая и вторая теоремы сравнения, признак Даламбера, радикальный и интегральный признаки Коши, признак Лейбница).
Исследовать на сходимость ряды:
1 . 2 . 3 .
4 . 5 . 6 .
