Практичне заняття 6 (Колоквіум) Основні закони розподілу випадкової величини Перелік питань
І. Основні закони розподілу випадкової величини
Біноміальний розподіл. Його числові характеристики.
Геометричний розподіл. Математичне сподівання, дисперсія, середнє квадратичне відхилення.
Гіпергеометричний розподіл. Його числові характеристики.
Розподіл Пуассона. Математичне сподівання, дисперсія, середнє квадратичне відхилення.
Нормальний закон розподілу. Його диференціальна та інтегральна функції, їх властивості та графіки. Числові характеристики. Правило „3-х σ”.
Рівномірний закон розподілу. Диференціальна та інтегральна функції. Числові характеристики.
Показниковий закони розподілу. Вигляд диференціальної та інтегральної функцій. Числові характеристики.
Розподіл
.
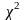Розподіл Ст’юдента.
Розподіл Фішера.
ІІ. Багатовимірні випадкові величини
Визначення багатовимірної випадкової величини та її закон розподілу.
Система двох дискретних випадкових величин, числові характеристики системи, кореляційний момент, коефіцієнт кореляції.
Функція розподілу ймовірностей та щільність ймовірностей системи.
Числові характеристики системи двох неперервних випадкових величин.
Дайте відповідь на запитання № ___________________________
____. _________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
____. _________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
____. _________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
____________________________________________________________________________________________________________________________________________________
__________________________________________________________________________
____________________________________________________________________________________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________