8.4. Розрахунок робочого колеса на міцність

Розрахунок радіально-осьового робочого колеса внаслідок його складної конфігурації і складного характеру розподілу діючих сил представляє великі труднощі. Методи розрахунку залежать від типів робочих коліс. Швидкохідні робочі колеса розраховують як систему закладених по кінцях кривих стержнів, що мають лопаті. Розрахунок виконується на ЕОМ. Завдання зводиться до визначення напруги у будь-якому перерізі лопаті у видгляді

_(8.22)

де М_r, М_у, J_r і J_у – згинальні моменти і моменти інерції у перерізі лопаті, відносно ОХ і OY; r і у - координати розрахункової точки; Р_розт - нормальна розтягуюча сила у перерізі; F_і - площа перерізу.

Моменти і сили в лопатях визначають як у стержнях, що мають геометричні характеристики лопаті, а обід замінюють многогранником із стержнів.

Рис. 8.5. До розрахунку робочого колеса на міцність

Розрахунок на міцність тихохідних робочих коліс, обід і ступицю можна розглядати як диски із криволінійними твірними, а короткі лопаті як оболонки, ведеться аналогічно розрахунку для робочих коліс компресорів і лопатевих насосів.

Крім того, при проектуванні використовують аналоги, близькі за формою і умовами експлуатації до нових типів.

При збільшенні розмірів для забезпечення динамічної міцності необхідно дотримуватися як геометричної подібності, так і критеріїв динамічної подібності сил. Найбільш достовірні дані можна отримати при випробуванні на міцність робочих діючих моделей і особливо на натурних гідротурбінах, працюючих на ГЕС.

Перевірку обода і ступиці на розрив під дією відцентрових сил (рис. 8.5) виконують при нормальній і розгінній частотах обертів, вважаючи рух у кожен момент таким, що встановився, систему урівноваженою і прирівнюючи масові сили до зовнішніх сил. Напруга у перерізі 1 - 1 визначається за формулами:

_(8.23)

де С_ст і С_об - відцентрові сили, що розвиваються масою половини колеса, і прикладені відповідно до ступиці і до обода.

Відцентрова сила, що діє на половину колеса

_(8.24)

де т_р.к - маса робочого колеса; п - частота обертів, об/хв; R_ц.в2 - радіус центру ваги половини робочого колеса.

Ця сила з умов квазистатичної рівноваги розподіляється між ступицею і ободом обернено пропорційно до відстаней по осі z від центру ваги колеса до центрів ваги цих елементів. Ці умови можна записати так

С_р.к=С_об+С_ст; С_об·z_об=С_ст·z_ст.

Вирішивши ці рівняння спільно, отримаємо

С_об=С_р.к·z_ст·(z_ст-z_об); С_ст=С_р.к·z_об·(z_ст-z_об); (8.25)

де відцентрові сили визначаються при п і п_розг, а радіус центру ваги половини колеса за формулою

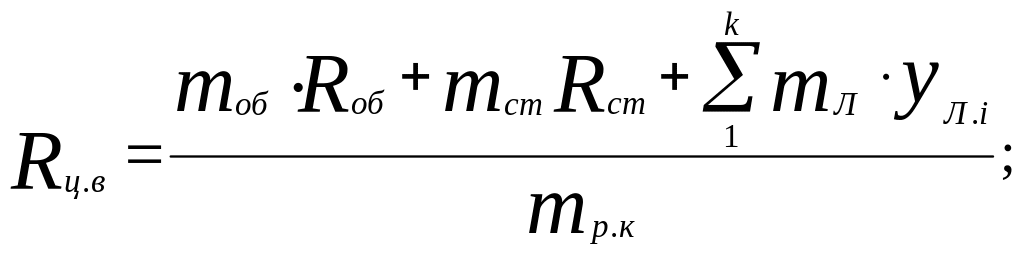_(8.26)

де т_об і т_ст – відповідно, маси обода і ступиці; R_об і R_ст - відстані від меридіанної розрахункової площини перерізу до центрів ваги половин цих елементів; у_л.і= R_Л·sіп α - те ж до центрів ваги лопатей; т_Л - маса лопаті; R_Л - радіус центру ваги лопаті; α - кут між розрахунковою площиною і радіусом, проведеним до центру ваги цієї лопаті; z - число лопатей.

Напругу визначають з формул при значеннях С_р.к як при нормальній, так і при розгінній частоті обертів:

С_р.об=С_р.к·z_об·[(z_ст+z_об)·F_об]; С_р.ст=С_р.к·z_ст·[(z_ст+z_об)·F_ст]; (8.27)

де F_ст і F_об – відповідно, площі розрахункових перерізів ступиці і обода.

Напруги у болтах ступиці роз'ємного колеса знаходять за формулою

С_р.б=С_ст·z_б·F'_б=4·С_ст=С_р.к[z_б·(d'_б)²·π]; (8.28)

де z_б - кількість болтів; F'_б - площа болта у перерізі, ослабленому різьбою; d'_б - внутрішній діаметр різьби.

Напруга у затягнутих болтах

σ_р.б.сум=σ_зат-χ·σ_р.б. (8.29)

Важливою умовою є умова нерозкрита стиків аж до розгінної частоти, при цьому напруга затягання визначається із формули

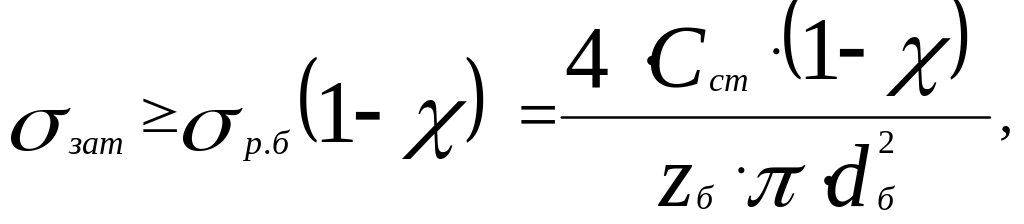_(8.30)

звідки можна визначити граничне значення відцентрової сили, що діє на ступиці

С_{ст.гран}= σ_зат·z_б· π·d²_б·(1-χ). (8.31)