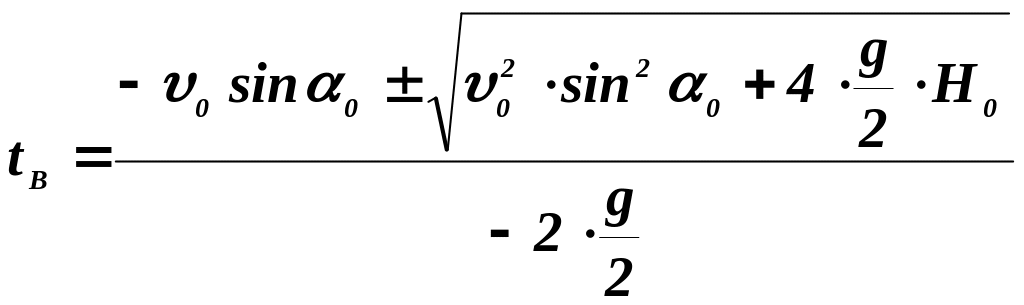С. С. Родионов, С. И. Родионова, Л.А. Корнеев, А.Е. Королев

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Курган – 2011

С. С. Родионов, С. И. Родионова, Л.А. Корнеев, А.Е. Королев

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Методические указания и контрольные

задания по разделу «Динамика»

К урган – 2011

УДК 531.8(07)

Р-60

Родионов С.С., Родионова С.И., Корнеев Л.А., Королев А.Е. Теоретическая механика. Методические указания и контрольные задания по разделу «Динамика». – Курган.: Изд-во КГСХА, 2011.- 32 с.

Рецензент профессор А.В. Фоминых

Методические указания составлены на основании рабочих программ курса теорической механики для направлении подготовки «Агроинжененрия», «Строительство», «Техносферная безопасность». В указаниях представлены задачи по наиболее важным темам «Динамики», из которых можно формировать задания для студентов, обучающихся по указанным выше направлениям.

Методические указания обсуждены и одобрены на заседании кафедры теоретической механики (протокол №8 от 27 апреля 2011 года), рассмотрены и рекомендованы к изданию методической комиссией факультета механизации сельского хозяйства (протокол № от 2011года).

© ФГБОУ ВПО «Курганская

государственная сельскохозяйственная

а кадемия имени Т. С. Мальцева», 2011

Содержание

ВВЕДЕНИЕ 6

ЗАДАЧА 1. дифференциальные уравнения движения точки 7

Задача 2. закон сохранения импульса 13

(количества движения точки) 13

ВВЕДЕНИЕ

Теоретическая механика является основой для изучения таких дисциплин, как сопротивление материалов, строительная механика, теория механизмов и машин, детали машин и др.

Настоящие методические указания содержат задания и примеры решения задач по наиболее важным разделам динамики: дифференциальные уравнения движения точки, общие теоремы динамики, принцип Даламбера, ПРИНЦИП Даламбера-Лагранжа.

Для выбора студентом задания следует пользоваться шифром, которым являются две последние цифры зачетной книжки (цифра 0 соответствует варианту 10).

Решение начинается с уяснения условия задачи, перенесенного без изменения из методических указаний, т.е. рисунков и всей информации из таблицы. Текст задачи, являющийся общим для всех, можно не приводить.

Далее выполняется чертеж (эскиз) конкретного задания, на котором все параметры (углы, размеры и т.д.) должны соответствовать конкретным условиям этого варианта. Чертеж должен быть крупным, аккуратным и наглядным, на нем должны быть показаны все обозначения, используемые в ходе решения задачи.

В тех случаях, когда приводится числовое значение физической величины, указывается, как правило, единица измерения. Например: 18 рад/с, 5 об. (оборотов), 3 с.

Если единица измерения не указывается, то подразумевается использование основной системной единицы. Например: S = 6t+23. В данном примере единица измерения длины - метр. Основными системными единицами являются также: с (секунда), м/с (метров в секунду), рад (радиан), Н (ньютон) и пр.

Если же необходимо воспользоваться внесистемной или не основной единицей измерения, то такую единицу измерения необходимо указывать во всех случаях. Например: t = 2t+4 (час.), n = 3000 об./мин., S = t²+15 (км).

Решения задач нужно сопровождать краткими пояснениями.

Задача 1. Дифференциальные уравнения движения точки

Материальная точка начинает движение в воздухе без сопротивления под углом ₀ к горизонту с начальной скоростью ₀ и на начальной высоте H₀

(рисунок 1).

Начальная скорость ₀ и масса m приведены в таблице 1, остальные данные - в таблице 2. Также в таблице 2 вопросительным знаком отмечены параметры, которые следует определить в ходе решения задачи.

Таблица 1 – Начальная скорость точки

Предпоследняя цифра шифра	0 , м/с
0	2,5
1	5
2	1,2
3	6
4	4,5
5	3,5
6	2,8
7	6,2
8	5,4
9	5,8

Таблица 2 – Исходные данные и искомые величины

Последняя цифра шифра	0,	H0, м	L, м	к,	к,	tп, с	tсп, с	Hmax, м	y=f(x)
0	0	5	?	?	?	?	?	?	?
1	-30	10	?	?	?	-	?	-	?
2	60	0	?	?	?	?	?	-	?
3	75	0	?	?	?	?	?	-	?
4	-80	20	?	?	?	-	?	-	?
5	-15	15	?	?	?	-	?	-	?
6	45	0	?	?	?	?	?	-	?
7	-60	12	?	?	?	-	?	-	?
8	85	10	?	?	?	?	?	?	-
9	-45	25	?	?	?	-	?	-	?

Видно, что в зависимости от варианта таблицы 2 следует определить некоторые из приведенных параметров: длину полета L, угол падения _к, конечную скорость _к, время подъема до максимальной высоты t_п, время спуска t_сп, максимальную высоту H_max, а также уравнение траектории y = f(x).

Рисунок 1 - Схема задачи

Пример 1

Материальная точка начинает движение под углом ₀ = 30 к горизонту на высоте H₀ = 2 м с начальной скоростью ₀ = 10 м/с.

Определить: L, _к, _к, t_п, t_сп, H_max , y = f(x).

Решение

Укажем материальную точку на траектории и укажем действующие на нее силы (рисунок 2). На точку действует только одна сила – сила тяжести .Запишем дифференциальные уравнения движения для осей x и y .

	(1)
	(2)

Рисунок 2 – Схема к примеру 1

Так как мы получим дифференциальные уравнения с разделяющимися переменными, решаем их, интегрируя два раза. Выполним первое интегрирование уравнения (1)

Возьмем интеграл

;

.

Т.к. m = const, m_x = const, то _x = const, т.е. величина _х принимает во все время движения неизмененное значение: такое же, как в начале движения.

x = 0x = 0∙ cos 0 .

(3)

Вычислим _x = ₀∙ cos ₀ = 10 ∙ cos 30 = 8,7 .

Таким образом, движение точки вдоль оси x является равномерным.

Решаем уравнение (2). Разделяем переменные

md_y = − mg ∙ dt или d_y = − g∙dt.

Интегрируем

y = − gt +C1.

(4)

Для определения константы С₁ используем условие

Подставляем эти значения в последнее выражение и вычисляем С₁:

_y0 = − g ∙ t₀ + C₁

₀ ∙ sin₀ = − g ∙ 0 + C₁;

C₁ = ₀ ∙ sin₀.

Уравнение (4) приобретает вид

y = − gt + 0 ∙ sin0.

(5)

Учитывая, что , переписываем уравнение (3)

.

Выполняем второе интегрирование

Начальные условия

Получаем C₃ = 0. Тогда

.

(6)

Точно так же, учитывая, что , получаем из формулы (5) уравнение

Решаем его

.

(7)

Начальные условия

Получаем C₄ = H₀.

Тогда уравнение (7) приобретает вид

.

(8)

Зависимости (6) и (8) описывают изменение координат x и y с течением времени. Формулы (3), (5) – это зависимости скоростей , от времени.

Определим t_п, используя эти зависимости.

В наивысшей точке _y = 0. подставим это значение в выражение (5).

Получим уравнение

.

(9)

Из него определим время подъема

.

Определим H_max. Подставим t_п в уравнение (8)

.

.

Определим полное время всего полета .

В месте падения y = 0. Подставим это значение в уравнение (8)

.

Решаем квадратное уравнение с неизвестным

(10)

Корни уравнения

Т.к. время полета должно быть > 0, то выбираем .

Определим время спуска t_сп

,

(11)

.

Определим длину полета L, для этого подставим время полета в уравнение (6).

L = ₀ ∙( cos ₀)∙ = 10 ∙ cos 30 ∙ 1,33 = 11,57 м.

Определим конечную скорость v_к по формуле

,

(12)

,

,

.

Определим угол падения _к.

,

Чтобы записать уравнение y = f(x), нужно выразить t из уравнения (6)

,

и подставить в уравнение (8)

.

После преобразований получим

(13)

где х – аргумент, м;

у – функция, м.

Видно, что траекторией является квадратная парабола.