3. Решение системы с помощью обратной матрицы

Дана система: (2.8)

Составим матрицу А из коэффициентов при неизвестных, матрицу-столбец Х – из неизвестных, матрицу-столбец В – из свободных членов.

,

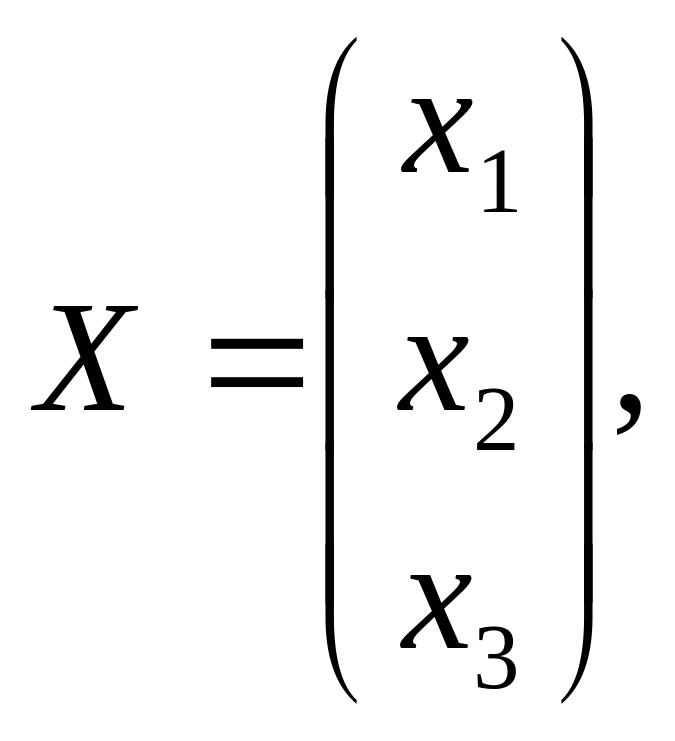
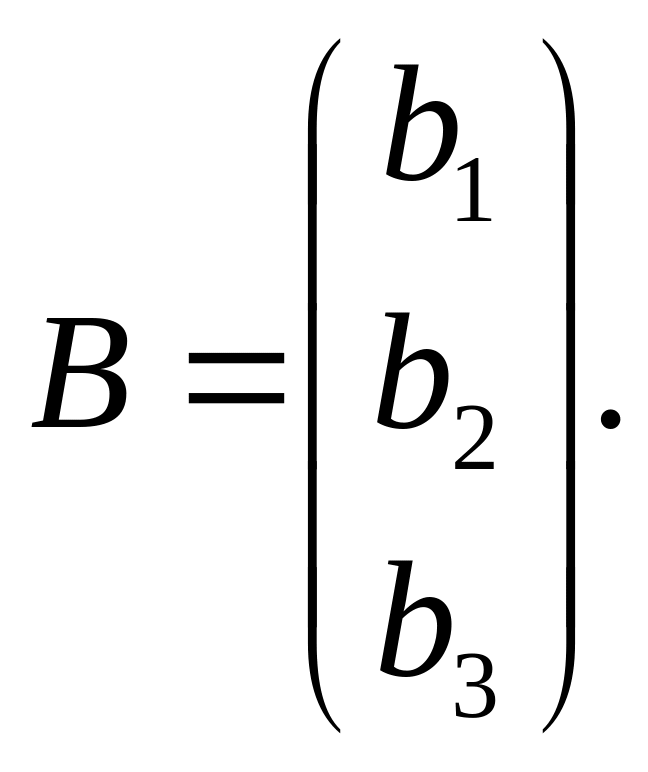
Систему (2.8) можно записать в матричной форме так:

Матрица-решение Х находится по формуле:

(2.9)

А^-1 – обратная матрица для матрицы А, она составляется из алгебраических дополнений элементов матрицы А по формуле (2.3):

– детерминант или определитель матрицы А, .

Пример 9. Решить систему:

Введем матрицы: ,

Обратная матрица вычислена в примере 6. По формуле (2.9) находим решение системы

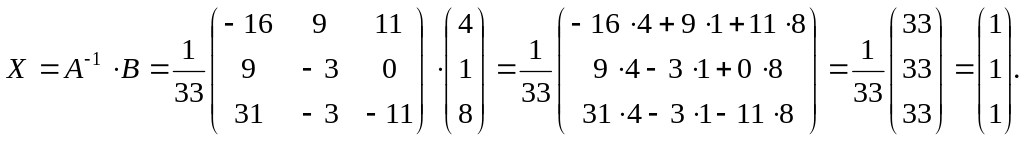
Итак, x₁=1, x₂=1, x₃=1.

3. Элементы векторной алгебры

Вектор – направленный отрезок; обозначается или . А – начало вектора, В – конец.

Длина или модуль вектора обозначается .

Рис. 21.

В координатном пространстве 0xyz вектор может быть представлен в виде

(3.1)

Эта формула дает разложение вектора по базису векторов , , ; , , - прямоугольные декартовые координаты вектора (иначе проекции вектора на оси координат).

Формулу (3.1) можно записать так:

– вектор имеет координаты , , .

Длина (модуль) вектора находится по формуле:

. (3.2)

Если вектор задан задан координатами начала A(x₁,y₁,z₁)и конца B(x₂,y₂,z₂), то координаты находятся по формулам:

(3.3)

Если известны разложения векторов и по осям координат , то при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются), при умножении вектора на число координаты вектора умножаются на это число, т.е.

(3.4)

Скалярным произведением векторов и , обозначается , называется число, равное произведению длин этих векторов на косинус угла между ними

. (3.5)

Если , , то

. (3.6)

Если векторы и коллинеарны (параллельны), то

. (3.7)

Если векторы и ортогональны (перпендикулярны), то

или (3.8)

Пример 10. Даны точки А₁(1,0,-1), A₂(2,-1,1), A₃(0,1,-2). Средствами векторной алгебры, учитывая, что найти:

1. координаты векторов и .

Используем формулу (3.3):

или ;

или .

2. Координаты вектора

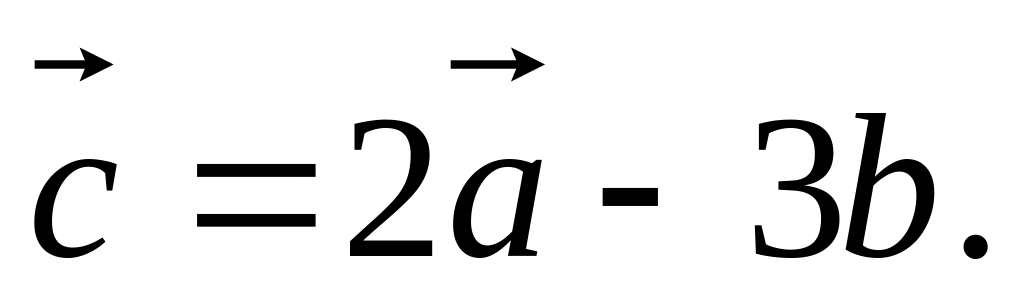
Используя формулы (3.4) и (3.5), получим

или

3. длину вектора

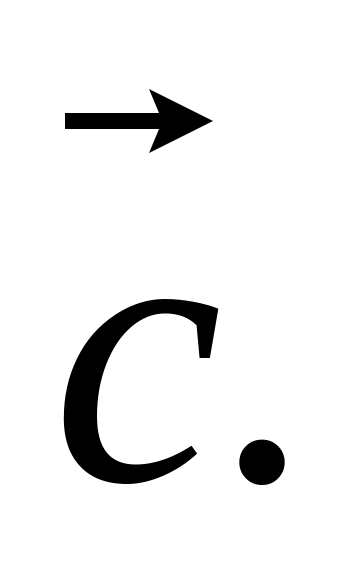
По формуле (3.2):

4. Скалярное произведение

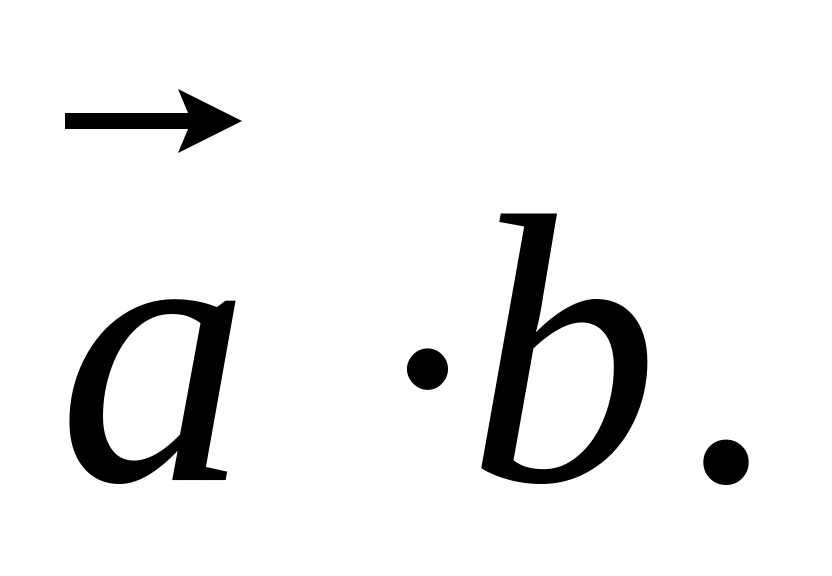
По формуле (3.6):

5. Проверить, коллинеарны или ортогональны векторы и

Проверяем условия (3.7) и (3.8).

векторы и неколлинеарны.

векторы неортогональны.