2. Элементы линейной алгебры

0. Определители второго и третьего порядка

Определителем второго порядка называется число, обозначаемое символом и определяемое равенством .

В определителе различают строки и столбцы. a₁₁, a₁₂, a₂₁, a₂₂ – элементы определителя. Каждый элемент снабжен двумя индексами: 1-й индекс обозначает номер строки, 2-ой – номер столбца, на пересечении которых стоит элемент.

Определителем третьего порядка называется число, обозначаемое символом

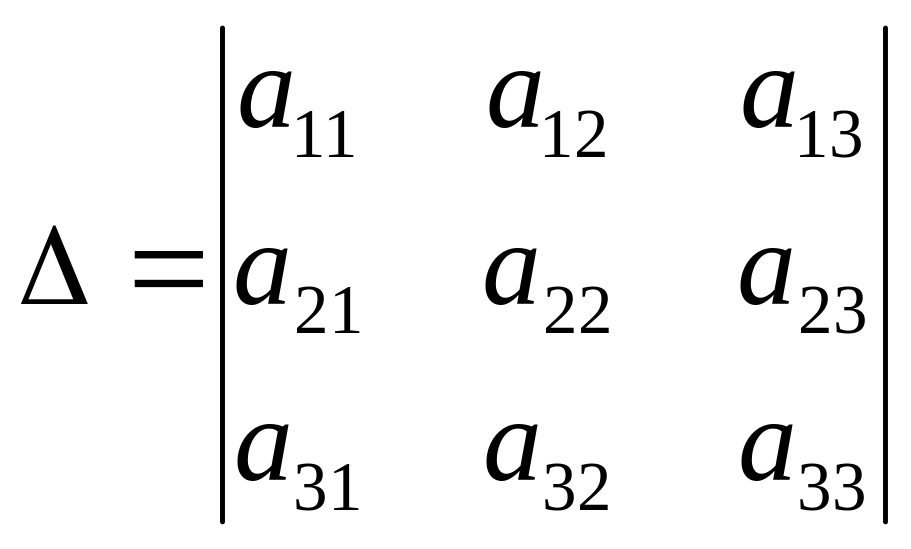
и определяемое равенством

(2.1)

Слагаемые формулы (2.1) составляются по схеме:

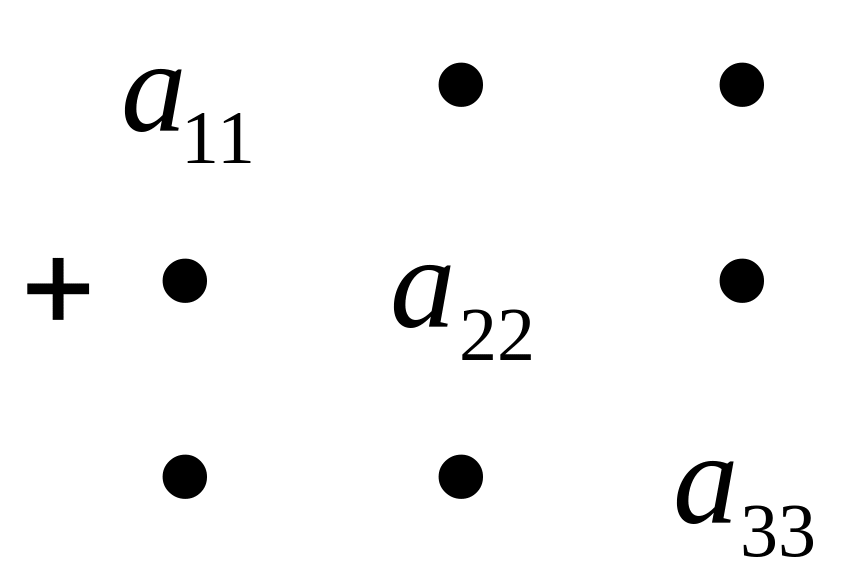
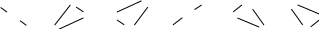EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3

В схеме знак «+» означает, что произведения указанных элементов берутся со своими знаками, а знак «-» – с противоположными (правило треугольников).

Пример 1. Вычислить определитель.

Минором M_ij элемента a_ij (i=1,2,3; j=1,2,3) определителя третьего порядка называется определитель второго порядка, который получается из определителя путем вычеркивания i-той строки и j-того столбца.

Например, если , то , .

Алгебраическим дополнением A_ij элемента a_ij определителя называется соответствующий минор M_ij, взятый со знаком (-1)^i+j, т.е.

Определитель можно вычислить по формуле разложения определителя по элементам 1-ой строки

. (2.2)

Определитель можно вычислить, разложив его по элементам любой строки или любого столбца, т.е. определитель равен сумме произведений элементов какой-либо строки (столбца) на алгебраические дополнения этих элементов.

Пример 2. Вычислить определитель по формуле (2.2).

0. Некоторые сведения о матрицах

Матрицей называется прямоугольная таблица, составленная из элементов.

.

Если матрица имеет строк и столбцов, то она имеет размер .

Если , то матрица называется квадратной порядка

Например,

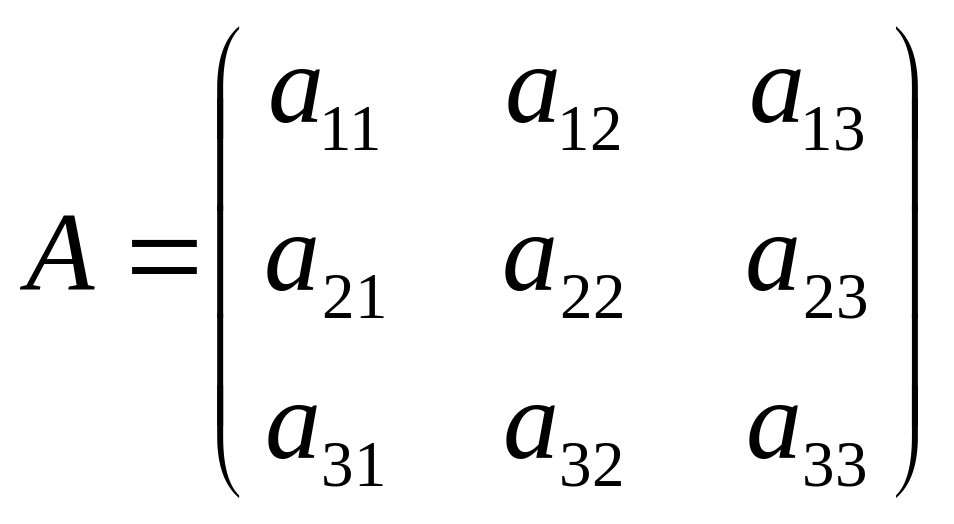– квадратная матрица 3-го порядка.

– матрица-строка. – матрица-столбец.

Две матрицы А и В называют равными (А=В), если они имеют одинаковые размеры и их соответствующие элементы равны.

Матрицы одинаковых размеров можно складывать (вычитать), при этом складываются (вычитаются) их соответствующие элементы.

= .

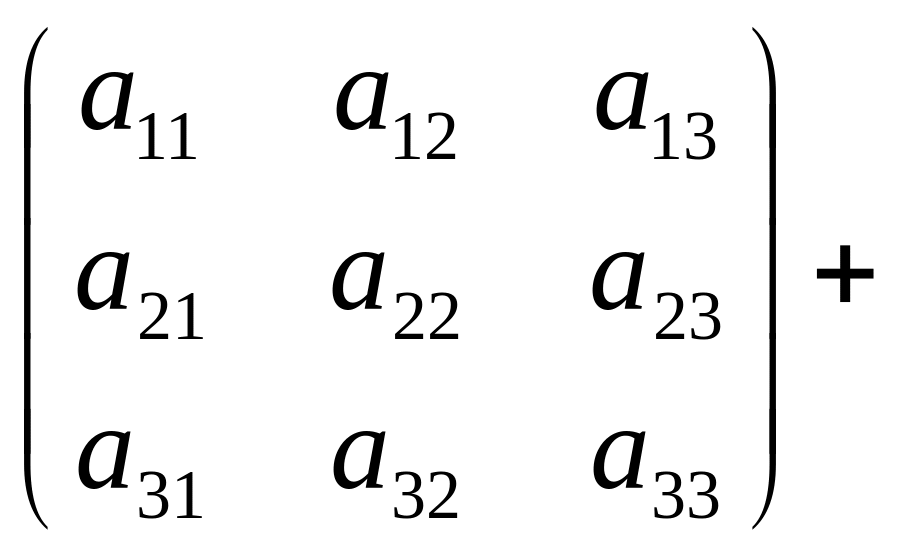
Матрицу можно умножить на число, при этом все элементы матрицы умножаются на это число.

.

Две матрицы можно умножить одну на другую только тогда, когда число столбцов 1-ой матрицы равно числу строк 2-ой матрицы, т.е. если размер 1-ой матрицы и 2-ой матрицы .

Умножение матриц производится по правилу: элемент i-той строки и j-того столбца матрицы произведения равен сумме произведений элементов i-той строки первого сомножителя на соответствующие элементы j-того столбца второго сомножителя.

Например, , .

.

Произведение матриц не подчиняется переместительному закону.

Для квадратной матрицы вводится определитель – детерминант этой матрицы, составленный из элементов матрицы.

Например, для матрицы :

.

Если , то матрица А называется невырожденной.

Пример 3. Даны две матрицы , .

Найти матрицу 2A – 3B.

. .

Пример 4. Дана матрица Найти det A.

Пример 5. Даны две матрицы ,

Найти произведение . Можно ли получить произведение ?

Число столбцов матрицы А равно числу строк матрицы В, следовательно можно найти произведение .

.

Произведение нельзя найти, т.к. число столбцов матрицы В не равно числу строк матрицы А.