0. Понятие о кривых второго порядка

Кривыми второго порядка на плоскости называются линии, которые аналитически определяются уравнениями второй степени, относительно переменных координат x и y. К ним относятся: окружность, эллипс, гипербола и парабола.

1.2.1. Окружность

Задача 8. Составить каноническое уравнение окружности с центром в точке С(a,b) и радиусом R.

Р ешение. M(x,y) – произвольная точка окружности. По определению окружности Найдем длину отрезка СМ. но , отсюда

(1.9)

– каноническое уравнение окружности.

Рис. 8.

Если центр окружности в т. О(0,0), то

(1.10)

– каноническое уравнение окружности с центром в начале координат.

1.2.2. Эллипс

Каноническое уравнение эллипса:

. (1.11)

2а – большая ось, а – большая полуось;

2b – малая ось, b – малая полуось;

2с – фокусное расстояние, с – полуфокусное расстояние.

b² = а² – с². (1.12)

A₁(a,0), A₂(-a,0), B₁(0,b), B₂(0,-b) – вершины, F₁(c,0), F₂(-c,0) – фокусы.

Рис. 9.

1.2.3. Гипербола

Гиперболой называют множество точек плоскости, координаты которых в некоторой системе координат удовлетворяют уравнению

(1.13)

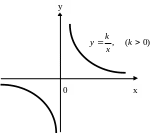
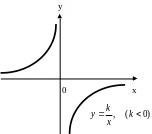
Рис. 10. Рис. 11.

1. Гипербола (13) не пересекает оси координат.

2. При k>0 график расположен в I и III координатных углах, а при k<0 – во II и IV.

3. Прямые x=0 и y=0 – оси координат являются асимптотами гиперболы.

Асимптотой кривой называется прямая, если расстояние от переменной точки М кривой до прямой стремится к нулю при неограниченном удалении точки М от начала координат по кривой.

4. Точка О(0,0) – центр симметрии гиперболы.

Уравнение

(1.14)

также определяет гиперболу на плоскости x0y. Это уравнение с помощью параллельного переноса осей координат

приводится к виду

(1.15)

З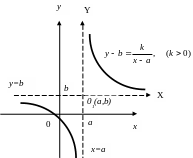 начит уравнение (14) определяет гиперболу в системе x0y, но ее центр находится в т. О(a,b), а асимптоты параллельны координатным осям и имеют уравнения x=a и y=b.

Рис. 12.

1.2.4. Гипербола как график дробно-линейной функции

Всякая дробно-линейная функция

(1.16)

может быть приведена к виду (14), значит ее графиком является гипербола.

Для приведения уравнения (16) к виду (14) надо выделить целую часть.

Задача 9. Уравнение гиперболы привести к виду , указать координаты центра и уравнения ее асимптот. Сделать чертеж.

Решение. Преобразуем данную функцию, разделив числитель на знаменатель:

Уравнение примет вид: Преобразуем дробь:

Уравнение примет вид: или

Используем формулы параллельного переноса Обозначим , - уравнение гиперболы относительно новой декартовой системы координат X0Y. x-2=0, y-3=0 – уравнения асимптот. O₁(2,3) – центр симметрии. k=3,5>0. Гипербола располагается в I и III четвертях относительно своих асимптот. Найдем точки пересечения гиперболы со старыми осями координат. Полагая в уравнении При Получили две точки: (0; 1,25), (5/6; 0) (рис. 13).

y

Y

0

x

2

Рис. 13.