2. Экстремумы функции

Функция имеет максимум (max) в точке x₀, если существует такая окрестность точки x₀, что для всех из этой окрестности выполняется неравенство .

Функция имеет минимум (min) в точке x₀, если существует такая окрестность точки x₀, что для всех из этой окрестности выполняется неравенство .

Максимумы и минимумы функции называются экстремумами.

Необходимое условие существования экстремума

Теорема. Если дифференцируемая функция имеет в точке x₀ экстремум, то .

Точки, в которых производная обращается в нуль или не существует, называются критическими точками.

Достаточные условия существование экстремума

Теорема 1. Если непрерывная функция имеет производную во всех точках некоторого интервала, содержащего критическую точку x₀ (кроме, быть может, самой точки x₀) и, если производная при переходе слева направо через критическую точку x₀ меняет знак с плюса на минус, то функция в этой точке имеет максимум; если же при переходе через точку x₀ производная меняет знак с минуса на плюс, то функция в этой точке имеет минимум.

Теорема 2. Если функция дважды дифференцируема в некоторой окрестности точки x₀ и , а , и, если , то в точке x₀ функция имеет max, если , то в точке x₀ функция имеет min

3. Выпуклость, вогнутость

График дифференцируемой функции называется выпуклым на интервале (a,b), если он расположен ниже любой своей касательной на этом интервале (рис.25).

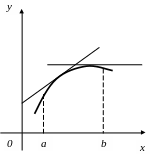
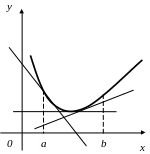
Рис. 25. Рис. 26.

График дифференцируемой функции называется вогнутым на интервале (a,b), если он расположен выше любой своей касательной на этом интервале (рис. 26).

Теорема. Пусть функция непрерывна вместе со своей производной на отрезке [a,b], и имеет в интервале (a,b) вторую производную .

Если во всех точках (a,b), то график функции в этом интервале выпуклый.

Если во всех точках (a,b), то график функции в этом интервале вогнутый.

Т очка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба (рис. 27).

Точка, в которой называется точкой, подозрительной на перегиб.

Рис.27.

4. План исследования функции

1. Найти область определения функции.

2. В случае, если область определения функции симметрична относительно начала координат, проверить, не является ли функция четной или нечетной.

3. Найти точки пересечения графика функции с осями координат.

4. Найти интервалы возрастания и убывания функции, точки экстремума.

5. Найти интервалы выпуклости и вогнутости графика функции, точки перегиба.

6. Определить поведение функции при 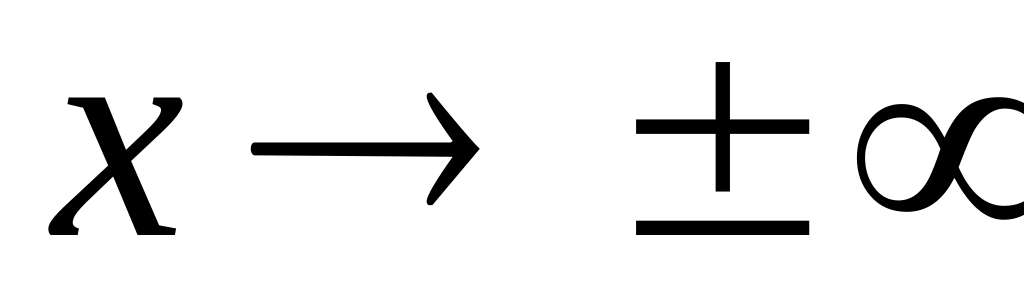, по необходимости вычислить дополнительно точки.

7. Построить график.

Задача

Исследовать и построить график функции

1. Область определения:

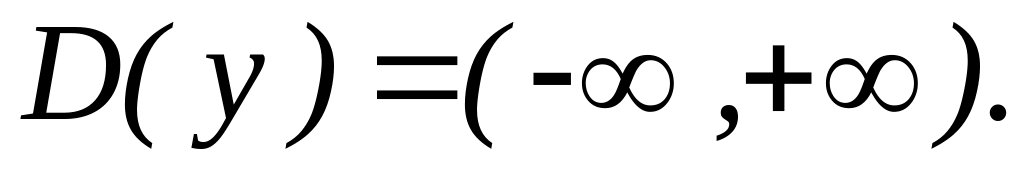
Функция определена и непрерывна при

2. 

– функция ни нечетная;

функция ни четная.

3. Найдем точки пересечения графика с осями координат.

С 0y:

c 0x:

График проходит через О(0;0), (3;0).

4. Найдем интервалы монотонности функции, точки экстремума.

точки, подозрительные на экстремум.

Функция убывает при , т.к.

функция возрастает при , т.к.

y_min =y(1)= -21³+121² -181 = -8.

y_man =y(3)= -23³+123² -183 = 0.

5. Найдем интервалы выпуклости, вогнутости и точки перегиба.

точка, подозрительная на перегиб.

y(2)= -22³+122² -182 = -4.

(2; -4) – точка перегиба графика функции.

График функции выпуклый при , т.к.

График функции вогнутый при , т.к.

6.

Видим, что при

при

7. Строим график.

Рис.28.