Правила дифференцирования
(5.18)
(5.19)
(5.20)
(5.21)
Производная сложной функции
Если
,
,
т.е.
– сложная функция y
от x,
то
.
(5.22)
Примеры. Найти производные функций.
1)
.
Применим формулу (5.18).
Найдем производные каждого слагаемого отдельно.
.
Вынесли постоянный
множитель за знак производной (5.20) и
применили (5.3). Далее объяснения
аналогичны.
;
; 
Итак,
2)
Применяя сначала формулу (5.19), затем формулы (5.4), (5.2), (5.8), (5.11), (5.1) таблицы, получим
3)
.
Применим формулу (5.21).
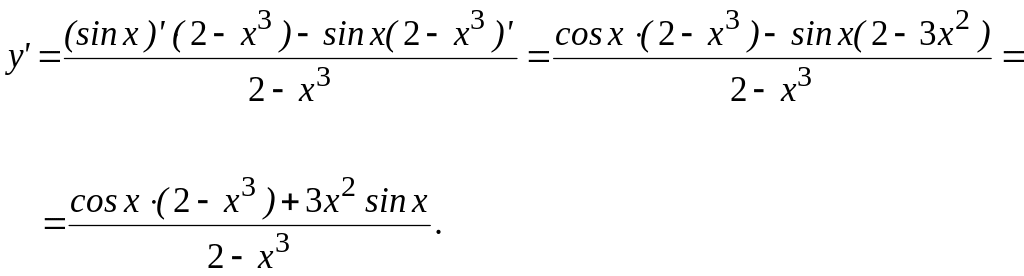
Найдем y’(0):
4)
Это сложная функция y от x.
Обозначим
Тогда имеем
Применим формулу (5.22):
5)
сложная
функция от x.
Обозначим
Итак,
Применим формулу (5.22):
6)
Обозначим
Итак,
Использованы формулы (5.22), (5.8), (5.14).
7)
Примеры для самостоятельного решения
Найти производные функций:
1)
.
2)
.
Найти
3)
. 4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
Дифференциал функции
Дана функция
,
где x
– независимая переменная. Приращение
независимой переменной
называется дифференциалом
независимой
переменной
и обозначается
.
Дифференциалом
функции
называется произведение
производной этой функции на дифференциал
независимой переменной, обозначается
или
.
или
Примеры. Найти дифференциалы функций
1)
;
2)
Функция обозначена буквой s
, аргумент – буквой t,
поэтому
.
3)
.
.
Примеры для самостоятельного решения
Найти дифференциалы функций:
1)
2)
3)
4)
5)
6)
Ответы:
1)
2)
3)
4)
5)
6)
6. Исследование функций одной переменной с помощью производных
Аналитические признаки возрастания и убывания функции
Функция
называется
возрастающей
на некотором промежутке X,
если из неравенства
,
где
,
– любые два значения из X
, следует неравенство
.
Функция
называется убывающей
на некотором промежутке X,
если из неравенства
,
где
,
– любые два значения из X
, следует неравенство
.
Необходимые условия возрастания и убывания функции
Теорема 1.
Если дифференцируемая в интервале (a,b)
функция
возрастает,
то
для
всех
Теорема 2.
Если
дифференцируемая в интервале (a,b)
функция
убывает,
то
для
всех
Достаточные условия возрастания и убывания функции
Теорема 1.
Если функция
непрерывна на отрезке [a,b]
и
для всех
,
то эта функция возрастает
на отрезке [a,b].
Теорема 2.
Если функция
непрерывна на отрезке [a,b]
и
для всех
,
то эта функция убывает
на отрезке [a,b].