Методические указания
Аналитическая геометрия
1.1. Прямая линия
1.1.1. Общее уравнение прямой
Если на плоскости взята декартова система координат, то всякое уравнение первой степени относительно текущих координат x и y
Ax + By + C = 0, (1.1)
где А и В одновременно не равны нулю, определяет прямую в этой системе координат.
Верно и обратное: в декартовой системе координат всякая прямая может быть задана уравнением первой степени вида (1.1).
Уравнение (1.1) – общее уравнение прямой.
Частные случаи
|
Значение коэффициентов |
Уравнение прямой |
Положение прямой |
1 |
С = 0 |
Ax + By = 0 |
Прямая проходит через начало координат |
2 |
А = 0 |
By + C = 0, y = - C/B, -C/B=b, y=b |
Прямая параллельна оси Ох |
3 |
В = 0 |
x = a, где a = -C/A |
Прямая параллельна оси Oy |
4 |
А = С = 0 |
y = 0 |
Прямая совпадает с осью Ox (уравнение оси Ох) |
5 |
В = С = 0 |
x = 0 |
Прямая совпадает с осью Oy (уравнение оси Oy) |
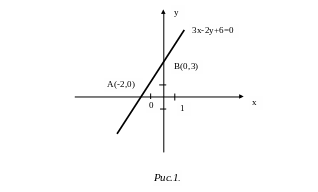
Задача 1. Построить прямую 3x-2y+6=0.
Решение. Для построения прямой достаточно знать какие-либо две ее точки, например, точки пересечения с осями координат.
Пусть y=0, тогда 3x+6=0, x=-2, A(-2,0) – лежит на оси Ох.
x=0, -2y+6=0, y=3, B(0,3) – лежит на оси Oy (рис. 1).
Уравнение прямой с угловым коэффициентом
У
глом
наклона прямой
к оси Ох
называется угол, на который надо повернуть
в положительном направлении ось Ох,
чтобы она совпадала с данной прямой
(или оказалась параллельной).
Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой и обозначается k.
(1.2)
Уравнение
(1.3)
называется уравнением прямой с угловым коэффициентом.
b – ордината точки пересечения прямой с осью Оу (рис.3,а)
При b=0 y=kx – уравнение прямой, проходящей через начало координат (рис.3, б).
При k=0 y=b – прямая параллельна оси Ох (рис. 3, в).
При k=b=0 y=0 – уравнение оси Ох.
x=a – уравнение прямой, параллельной оси Оу (рис.3, г).
x=0 – уравнение оси Оу.
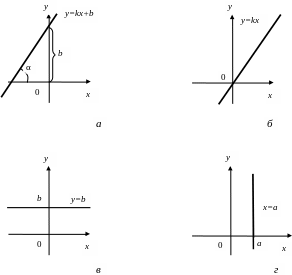
Рис. 3.
Замечание. Чтобы найти угловой коэффициент прямой, заданной общим уравнением, надо привести его к виду y=kx+b (т.е. разрешить относительно y).
Задача 2. Найти угловой коэффициент прямой 2x-3y+5=0.
Решение. Выразим из уравнения y:
