Вариант XVI
а. Исследовать и решить систему уравнений:
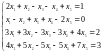
б.
Найти фундаментальную систему решений:
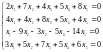
с.
Решить матричное уравнение:
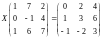
Найти собственные значения и собственные векторы матрицы:
Показать, что векторы
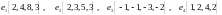образуют базис и найти координаты
вектора
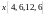в этом базисе.а. Линейное преобразование в базисе имеет матрицу
.
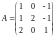Найти матрицу этого преобразования в
базисе
,
если
,
,
.
Вариант XVII
а. Исследовать и решить систему уравнений:
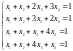
б.
Найти фундаментальную систему решений:
с.
Решить матричное уравнение:
Найти собственные значения и собственные векторы матрицы:
Найти размерность и базис подпространства, натянутого на систему векторов:
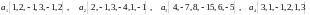.а. Линейное преобразование в базисе имеет матрицу
.
Найти матрицу этого преобразования в
базисе
,
если
,
,
.
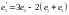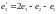Вариант XVIII
а. Исследовать и решить систему уравнений:
б.
Найти фундаментальную систему решений:
с.
Решить матричное уравнение:
Найти собственные значения и собственные векторы матрицы:
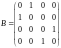
Определить базис и размерность суммы и пересечения подпространств, натянутых на векторы:
и
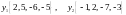.а. Линейное преобразование в базисе имеет матрицу
.
Найти матрицу этого преобразования в
базисе
,
если
,
,
.
Вариант XIX
а. Исследовать и решить систему уравнений:
б.
Найти фундаментальную систему решений:
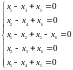
с.
Решить матричное уравнение:
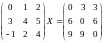
Найти собственные значения и собственные векторы матрицы:
Определить базис и размерность суммы и пересечения подпространств, натянутых на векторы:
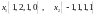и
.а. Линейное преобразование в базисе имеет матрицу
.
Найти матрицу этого преобразования в
базисе
,
если
,
,
.
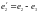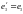Вариант XX
а. Исследовать и решить систему уравнений:
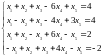
б.
Найти фундаментальную систему решений:
с.
Решить матричное уравнение:
Найти собственные значения и собственные векторы матрицы:
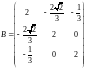
Найти размерность и базис подпространства, натянутого на систему векторов:
.а. Линейное преобразование в базисе имеет матрицу
.
Найти матрицу этого преобразования в
базисе
,
если
,
,
.
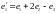
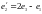
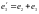