
Вариант I
а. Исследовать и решить систему уравнений:

б.
Найти фундаментальную систему решений:

с.
Решить матричное уравнение:
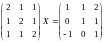
Найти собственные значения и собственные векторы матрицы:

Показать, что векторы
 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
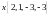 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования (в базисе, в котором заданы координаты всех векторов), переводящего векторы
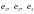 в векторы
в векторы
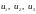 соответственно:
соответственно:

Вариант II
а. Исследовать и решить систему уравнений:

б.
Найти фундаментальную систему решений:
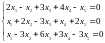
с.
Решить матричное уравнение:
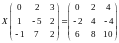
Найти собственные значения и собственные векторы матрицы:
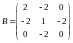
Показать, что векторы
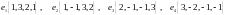 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования, переводящего векторы
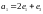 ,
,
 ,
,
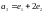 соответственно в векторы
соответственно в векторы
 ,
,
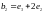 ,
,
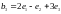 .
.
Вариант III
а. Исследовать и решить систему уравнений:

б.
Найти фундаментальную систему решений:
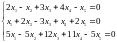
с.
Решить матричное уравнение:

Найти собственные значения и собственные векторы матрицы:
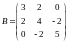
Показать, что векторы
 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
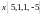 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования (в базисе, в котором заданы координаты всех векторов), переводящего векторы в векторы соответственно:
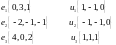
Вариант IV
а. Исследовать и решить систему уравнений:

б.
Найти фундаментальную систему решений:
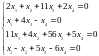
с.
Решить матричное уравнение:

Найти собственные значения и собственные векторы матрицы:

Показать, что векторы
 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
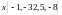 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования (в базисе, в котором заданы координаты всех векторов), переводящего векторы в векторы соответственно:
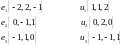
Вариант V
а. Исследовать и решить систему уравнений:

б.
Найти фундаментальную систему решений:

с.
Решить матричное уравнение:
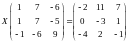
Найти собственные значения и собственные векторы матрицы:

Показать, что векторы
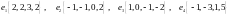 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования (в базисе, в котором заданы координаты всех векторов), переводящего векторы в векторы соответственно:

ВАРИАНТ VI
а. Исследовать и решить систему уравнений:

б.
Найти фундаментальную систему решений:

с.
Решить матричное уравнение:
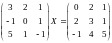
Найти собственные значения и собственные векторы матрицы:
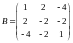
Показать, что векторы
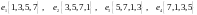 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
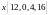 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования, переводящего векторы
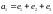 ,
,
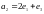 ,
,
 соответственно в векторы
соответственно в векторы
 ,
,
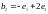 ,
,
 .
.
ВАРИАНТ VII
а. Исследовать и решить систему уравнений:

б.
Найти фундаментальную систему решений:
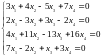
с.
Решить матричное уравнение:
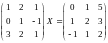
Найти собственные значения и собственные векторы матрицы:
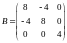
Показать, что векторы
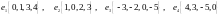 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
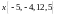 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования, переводящего векторы
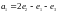 ,
,
 ,
,
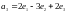 соответственно в векторы
соответственно в векторы
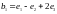 ,
,
 ,
,
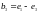 .
.
ВАРИАНТ VIII
а. Исследовать и решить систему уравнений:

б.
Найти фундаментальную систему решений:

с.
Решить матричное уравнение:
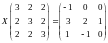
Найти собственные значения и собственные векторы матрицы:
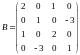
Показать, что векторы
 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
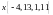 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования, переводящего векторы
 ,
,
 ,
,
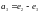 соответственно в векторы
соответственно в векторы
 ,
,
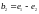 ,
,
 .
.
ВАРИАНТ IX
а. Исследовать и решить систему уравнений:
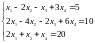
б.
Найти фундаментальную систему решений:

с.
Решить матричное уравнение:
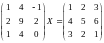
Найти собственные значения и собственные векторы матрицы:

Показать, что векторы
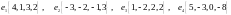 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
 в этом базисе.
в этом базисе.а. Найти матрицу линейного преобразования, переводящего векторы , , соответственно в векторы , ,
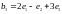 .
.
