
- •Глава 3. Характеристика основных типов статистических прогнозирующих математических моделей
- •3.1. Регрессионные статистические модели временных рядов (ar-, ari-, arx-, armax-, arma-, arima-, arimax- модели процессов)
- •3.2. Модели экспоненциального сглаживания Брауна, взвешенного среднего, Холта – Уинтерса и подобные
- •3.3. Спектральные статистические модели (канонические разложения, разложение Карунена – Лоэва, модели компонентного и факторного анализов)
- •3.4. Обобщенный фильтр Винера (метод прогнозирования Заде – Рагаззини)
- •3.5. Прогнозирующий фильтр Калмана (фильтр Калмана – Бьюси)
- •3.6. Модель многомерной (векторной) регрессии
- •3.7. Модели кластерного анализа и теории распознавания образов
- •Литература к главе 3
- •Глава 4. Характеристика основных типов детерминированных прогнозирующих математических моделей
- •4.1. Формулировка условия для эффективного применения детерминированного подхода решения проблемы прогнозирования
- •4.2. Характеристика основных типов детерминированных прогнозирующих математических моделей
- •4.2.1. Составляющие детерминированных временных рядов
- •4.2.2. Полиномиальные модели
- •4.2.3. Конечные гармонические ряды Фурье
- •4.2.4. Детерминированные модели спектрального разложения по ортогональным функциям, декомпозиционный метод моделирования
- •4.2.5. Нейросетевая модель и модели на основе нечетких множеств
- •4.2.6. Модели процессов на основе метода группового учета аргумента (мгуа)
- •4.2.7. Модели на основе алгебраических регрессионных зависимостей
- •4.2.8. Метод сингулярного спектрального анализа (метод Caterpillar или «гусеницы»)
- •Заключение
- •Литература к главе 4
- •Глава 5. Характеристика основных типов комбинированных вероятностно-детерминированных прогнозирующих математических моделей процессов
- •5.1. Комбинированные вероятностно-детерминированные модели
- •5.2. Характеристика основных типов комбинированных вероятностно-детерминированных математических моделей
- •5.3. Выводы по анализу прогнозирующих математических моделей процессов
- •Литература к главе 5
Глава 3. Характеристика основных типов статистических прогнозирующих математических моделей
В настоящей главе дается общая классификация и анализ статистических (вероятностных) математических моделей, используемых для краткосрочного и оперативного прогнозирования параметров объектов и процессов, в частности, электропотребления предприятий и энергосистем.
Подробно анализируются модели временных рядов, составляющие основу статистических прогнозирующих математических моделей случайных процессов, в частности: AR-, ARMA-, ARIMA-, МА-модель и модели взвешенного скользящего среднего, экспоненциального сглаживания Брауна и т.п. Как многофакторные рассматриваются: ARX-модели, ARMAX-модели и т.п. На реальных данных показана применимость ARIMA-моделей для прогноза графиков нагрузки энергосистем и предприятий. Однако структурную устойчивость данная модель сохраняет, если для приведения моделируемого процесса к стационарному виду используются разности порядка d<2.
Анализируются прогнозирующие модели функционирования объектов и систем, основанные на фильтрах Калмана и Винера (модель Заде – Рагаззини); спектральных ортогональных разложениях, в том числе, Карунена – Лоэва; каноническом разложении случайного процесса; многомерной регрессии; теории кластерного анализа; теории распознавания образов.
При статистической
параметрической идентификации случайного
процесса важен вопрос определения
характеристик точности, полученных
оценок параметров модели и их зависимость
от объема предыстории. Эта информация
необходима, например, для принятия
решения об окончании идентификации
объекта, а также при выборе той или иной
модели. Наиболее полные данные об этом
содержатся в многомерной плотности
вероятности
 оценки параметров
оценки параметров
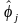 модели случайного процесса [9]. Однако,
предполагая нормальность этого
распределения вероятности, его без
потери информации характеризуют
числовыми характеристиками:
модели случайного процесса [9]. Однако,
предполагая нормальность этого
распределения вероятности, его без
потери информации характеризуют
числовыми характеристиками:
математическим ожиданием
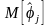 ;
;смещением
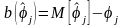 ;
;корреляционной матрицей
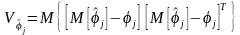 .
.
Косвенными характеристиками, определяющими желаемые свойства полученных параметров, являются [9, 10, 65]:
несмещенность, показывающая, что для каждого параметра вектора среднее значение по множеству реализаций совпадает с истинным значением параметра
 :
:
 или асимптотическая несмещенность:
или асимптотическая несмещенность:
 ;
;состоятельность, определяющая, что оценка с увеличением объема выборки или ростом j сходится по вероятности к истинному значению :
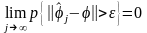 ,
,
или, иначе, состоятельность при асимптотической несмещенности определяет стремление к нулю дисперсии ошибок оценивания параметров
 ,
,
где
 – след матрицы
– след матрицы
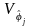 ;
;
эффективность, показывающая, что оценка параметров в классе
 всех несмещенных оценок параметров
обладает минимальной дисперсией:
всех несмещенных оценок параметров
обладает минимальной дисперсией:
 .
.
Если эффективность
имеет место только при
 ,
то ее называют асимптотической.
,
то ее называют асимптотической.
Перечисленные характеристики являются определяющими факторами при выборе той или иной математической модели объекта и алгоритма идентификации в конкретных случаях.
Так, известно [9], что МНК при оценивании параметров динамических объектов приводит в общем случае к смещенным оценкам, но это не является полным препятствием к использованию этого метода. При малой интенсивности шумов точность оценивания параметров, как правило, оказывается достаточной для практических задач и т.д. Приведем краткое описание моделей, перечисленных на рис. 2.1.
