3. Коэффициенты ассоциации и контингенции.

Область применения: применяются для изучения взаимосвязи двух качественных признаков, представленных в дихотомической шкале (принимают только два значения).

Расчетная формула:

Для их вычисления строится таблица, которая показывает связь между двумя признаками (явлениям), каждое из которых должно быть альтернативным («да» - «нет», «хороший» - «плохой»):

A	b	a+b
C	d	c+d
a+c	b+d	a+b+c+d

Коэффициенты вычисляются по формуле:

• ассоциации:

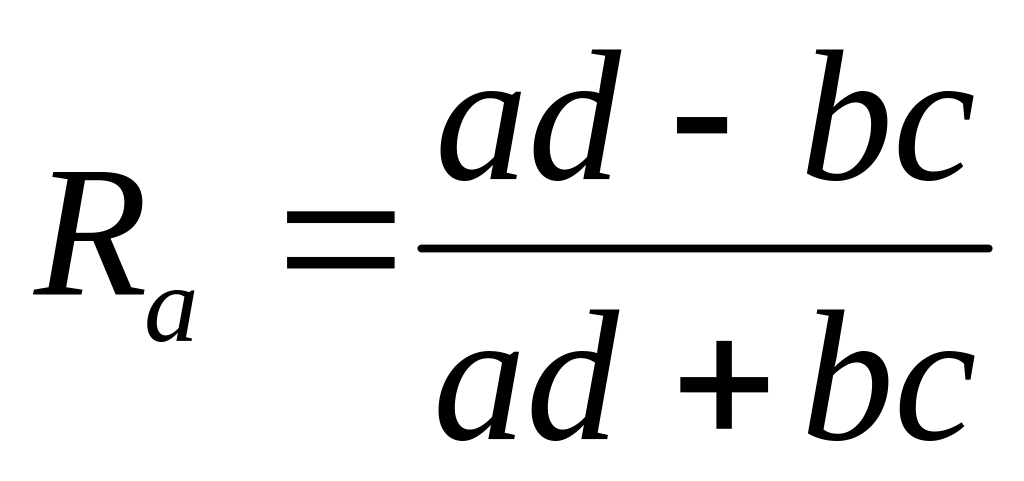
• контингенции:

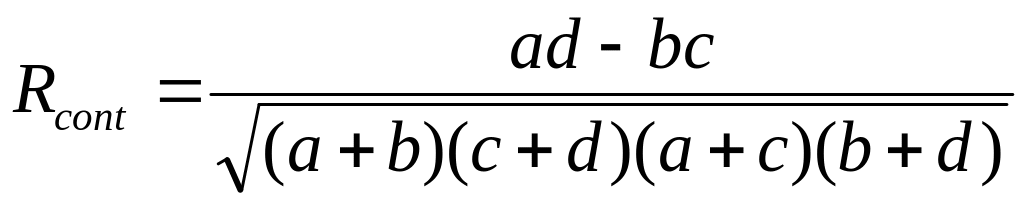
Свойства коэффициентов:

1. Изменяются в пределах от –1 до +1.

2. Коэффициент ассоциации всегда больше коэффициента контингенции.

3. Связь считается существенной, если 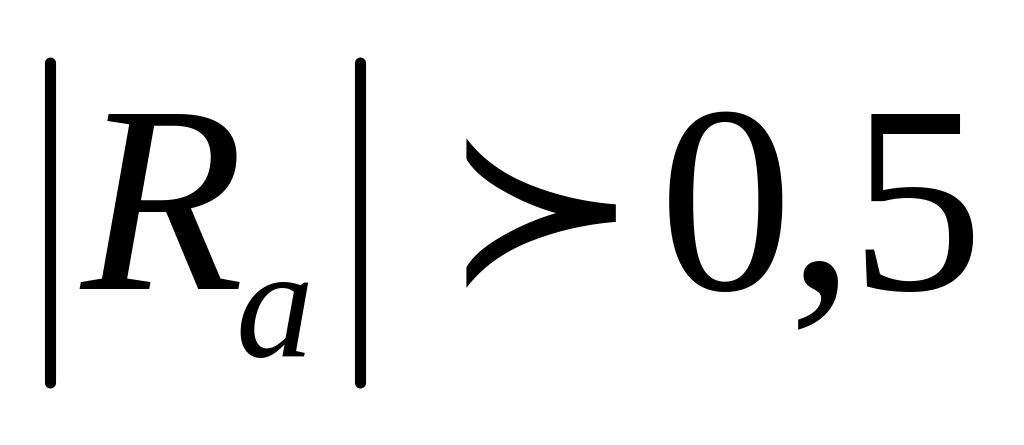или

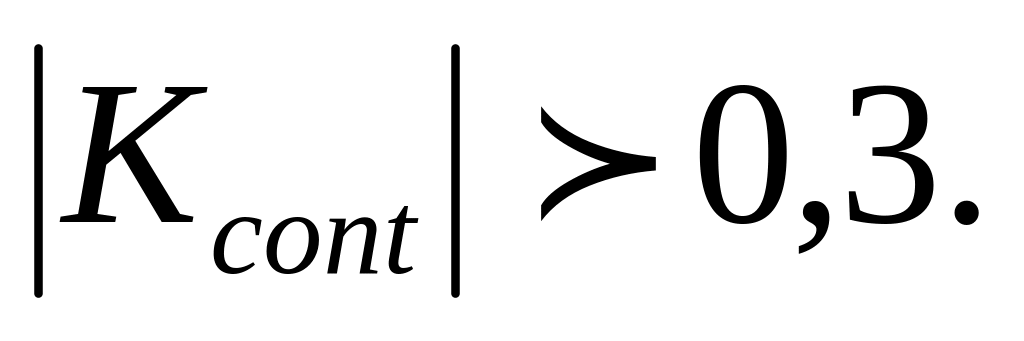
4. Знак коэффициентов интерпретации не имеет.

Проверка гипотезы о значимости выборочного коэффициента контингенции.

Алгоритм:

1. Н₀: связь следует признать незначимой;

Н₁: связь следует признать значимой, коэффициентам и выводам можно доверять.

2. .

3 . .

4. ОПГ КО

4.Бисериальный коэффициент корреляции.

Область применения: применяется для изучения взаимосвязи между двумя признаками, один из которых измеряется в дихотомической шкале (Х), а другой - в шкале интервалов или отношений (У).

Расчетная формула:

, где

– среднее значение по тем элементам переменной Y, которым соответствует код (значение признака) «1» в переменной Х;

– среднее значение по тем элементам переменной Y, которым соответствует код (значение признака) «0» в переменной Х;

σ_y – среднее квадратическое отклонение признака Y, вычисляемое по формуле:

σ_у =

n₁ – количество значений переменной X, которым соответствует код «1»;

n₀ – количество значений переменной X, которым соответствует код «0»;

n= n₁ + n₀ – общее количество значений переменной X.

Свойства коэффициента:

1. Изменяется в пределах от –1 до +1.

2. Знак коэффициента для интерпретации не имеет значения.

3. Характеризует тесноту связи:

Значение коэффициента корреляции	Характер связи
Rb = 0	Отсутствует
0 < | Rb | ≤ 0,3	Слабая
0,3 < | Rb | ≤ 0,6	Средняя
0,6 < | Rb | < 1	Сильная
| Rb | = 1	Функциональная

Проверка гипотезы о значимости выборочных коэффициентов ассоциации и контингенции.

Алгоритм:

1. Н₀: (отсутствии корреляционной связи между исследуемыми переменными в генеральной совокупности), Н₁: .

2. ;

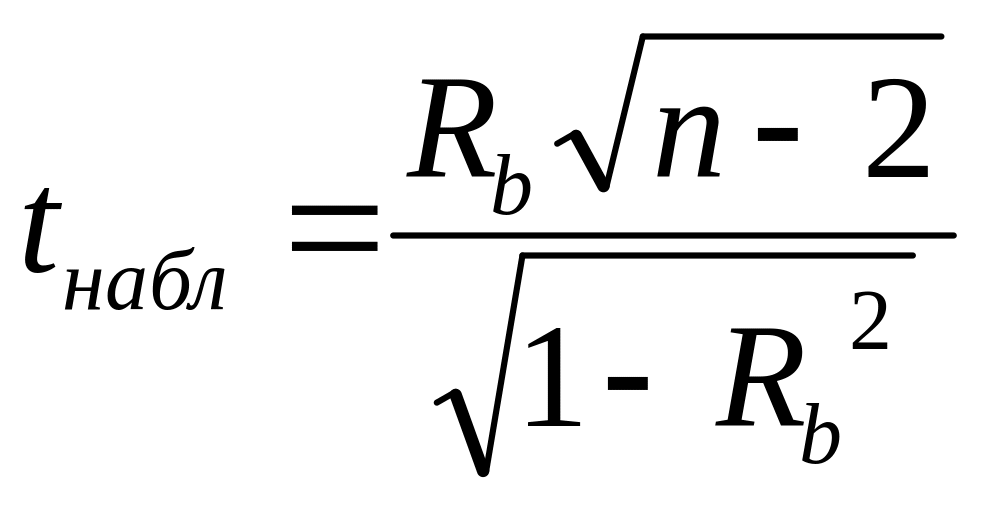3. , ;

4. КО ОПГ КО

-t_кр t_кр t

5. Рангово - бисериальный коэффициент корреляции Кертена и Гласса (Rrb).

Область применения: применяется для изучения взаимосвязи между двумя признаками, один из которых измеряется в дихотомической шкале (Х), а другой - в ранговой шкале (У).

Расчетная формула:

, где

– средний ранг по тем элементам переменной Y, которым соответствует код (значение признака) 1 в переменной Х;

– средний ранг по тем элементам переменной Y, которым соответствует код (значение признака) 0 в переменной Х;

n –объем выборки.

Свойства коэффициента:

1) Изменяется в пределах от –1 до +1.

2) Знак коэффициента для интерпретации не имеет значения.

3) Характеризует тесноту связи:

Значение коэффициента корреляции	Характер связи
Rrb = 0	Отсутствует
0 < | Rrb | ≤ 0,3	Слабая
0,3 < | Rrb | ≤ 0,6	Средняя
0,6 < | Rrb | < 1	Сильная
| Rrb | = 1	Функциональная

Проверка гипотезы о значимости выборочных коэффициентов ассоциации и контингенции.

Алгоритм:

1. Н₀: (отсутствии корреляционной связи между исследуемыми переменными в генеральной совокупности), Н₁: .

2. ;

3. , ;

4. КО ОПГ КО

-t_кр t_кр t